Uma expressão desenvolvida de potencial químico para deformação rápida em eletrodos de nanopartículas de baterias de íon-lítio

Resumo

Neste trabalho, propomos uma expressão desenvolvida de potencial químico sem a suposição de baixa taxa de deformação para explicar o estresse induzido pela difusão e a distribuição da concentração de Li em eletrodos de nanopartículas de baterias de íon-lítio. A diferença entre as expressões desenvolvidas e tradicionais sobre a evolução das tensões em um eletrodo de nanopartículas esféricas de silício é analisada tanto em operações potenciostáticas quanto galvanostáticas, usando a equação de difusão derivada e a teoria de deformação finita. O resultado numérico sugere que a diferença entre essas duas expressões de potencial químico é significativa em operação potenciostática, ao invés de em operação galvanostática. Um raio crítico, onde não há diferença entre o fluxo de Li causado por essas duas expressões de potencial químico, bem como a tensão hidrostática de Cauchy durante a maior parte do processo litiado, é primeiramente relatado neste trabalho.

Introdução

Para o desenvolvimento de dispositivos eletrônicos portáteis, veículos elétricos e armazenamento de energia em grande escala, uma série de materiais de eletrodo de alta capacidade, como o silício, que sofrem mudanças extremas de volume durante a litiação, são propostas para serem aplicadas em baterias de lítio [1,2 , 3]. A tensão induzida pela deformação volumétrica homogênea é chamada de tensão induzida por difusão, que pode induzir a fratura frágil durante a carga e descarga cíclicas, e este efeito negativo degrada ainda mais a capacidade da bateria [4]. Os materiais compostos dos eletrodos da bateria de íon-lítio são geralmente complexos e suas morfologias são diferentes, o que torna mais difícil explicar o comportamento da bateria por teoria ou equação. Em modelos teóricos, as propriedades dos materiais compósitos são geralmente simuladas considerando as mudanças dos parâmetros do material do eletrodo nas coordenadas espaciais, enquanto o efeito da interface dos materiais compósitos é ignorado. Atualmente, três formas típicas de eletrodo, isto é, esférica, cilíndrica e em placa, são consideradas principalmente no modelo teórico. Entre eles, as formas esféricas e cilíndricas são geralmente modelos unidimensionais, e modelos unidimensionais e bidimensionais para eletrodos de placa estão disponíveis. Recentemente, uma série de estudos se concentrou no estresse induzido por difusão em eletrodos de nanopartículas de silício de baterias de íon-lítio. Por exemplo, Yang et al. [5] apresentaram um modelo quimiomecânico para investigar a transformação de fase induzida por litiação, evolução morfológica, geração de tensões e fratura em nanofios de silício cristalino. Li et al. [6] estudaram o efeito da velocidade local no estresse induzido pela difusão em eletrodos de nanopartículas de silício. Zhao et al. [7] analisaram a tensão induzida por difusão considerando a deformação inelástica do material hospedeiro. Em todos esses trabalhos citados, a física fundamental envolvida é a difusão atômica ou iônica em sólidos sob múltiplas forças motrizes. A difusão atômica em um sólido pode alterar a composição sólida de seu estado estequiométrico e ser afetada pelo estresse induzido pela difusão. Essa interação de tensão e difusão é governada pelo equilíbrio termodinâmico dos sólidos.

Larche e Cahn [8] desenvolveram uma estrutura termodinâmica para sólidos multicomponentes que alcançam o equilíbrio sob estresse não hidrostático. A estrutura foi baseada na suposição de que a deformação causada pela mudança de composição é pequena e isotrópica. Como resultado, um potencial químico dependente do estresse foi introduzido para explicar a interação entre o estresse e a difusão. Wu [9] derivou um potencial químico dependente da tensão diferente no qual o tensor de momento de Eshelby está envolvido em vez da tensão de Cauchy hidrostática. Com base nisso, Cui et al. [10] propuseram um novo potencial químico para a deformação finita de sólidos. No entanto, nesses trabalhos, a derivação só deve ser rigorosa quando a deformação é pequena ou a taxa de deformação é baixa o suficiente em comparação com a difusão. É provável que cometa um erro significativo para um eletrodo de silício por causa de sua grande expansão volumétrica composicional (∼ 400%) quando é litiado rapidamente.

Neste trabalho, apresentamos uma expressão desenvolvida de potencial químico sem a suposição de baixa taxa de deformação, diferenciada da expressão tradicional de Cui [10]. Este modelo é estabelecido para a deformação rápida dos eletrodos durante a carga ou descarga e é independente das morfologias porque o potencial químico é uma quantidade intensiva ao invés de uma quantidade extensa. A diferença entre essas duas expressões de potencial químico nas distribuições de estresse e concentração de Li são analisadas em ambas as operações potenciostática e galvanostática em eletrodos de nanopartículas de Si. O resultado revela que a diferença aumenta com o aumento da taxa de deformação. Um raio crítico, onde não há diferença entre o fluxo de Li causado por essas duas expressões de potencial químico, bem como a tensão hidrostática de Cauchy durante a maior parte do processo litiado, é encontrado ao mesmo tempo.

Métodos

Equações mecânicas

A inserção de lítio nos eletrodos pode causar alteração volumétrica. Por conveniência, empregamos duas maneiras de descrever a deformação e o movimento dos sólidos, a saber, a descrição Lagrangiana e a descrição Euleriana. O movimento das partículas materiais em um meio contínuo pode ser descrito por
$$ \ mathbf {U} =\ mathbf {x} - \ mathbf {X} $$ (1)
onde x são as coordenadas de Euler, X são as coordenadas de Lagrange e U é o campo de deslocamento. A mudança na forma do sólido contínuo pode ser caracterizada pelo tensor de gradiente de deformação, dado por
$$ \ mathbf {F} =\ frac {\ partial \ mathbf {x}} {\ partial \ mathbf {X}} =\ mathbf {I} + \ mathrm {Grad} \ mathbf {U}, $$ (2 )
onde Grad representa o operador gradiente na descrição Lagrangiana, e I é o tensor unitário de segunda ordem.

Para uma partícula esférica, as coordenadas de Lagrange e as coordenadas de Euler de um ponto material são (R, Θ, Φ) e (r, θ, φ) respectivamente no sistema esférico. Então, o tensor de gradiente de deformação F é encontrado como
$$ \ mathbf {F} =\ left [\ begin {array} {ccc} {F} _R &0 &0 \\ {} 0 &{F} _ {\ Theta} &0 \\ {} 0 &0 &{F} _ {\ Phi} \ end {array} \ right] =\ left [\ begin {array} {ccc} 1+ \ parcial u / \ parcial R &0 &0 \\ {} 0 &1 + u / R &0 \\ {} 0 e 0 e 1 + u / R \ end {array} \ right]. $$ (3)
Durante a carga ou descarga, a mudança de forma do eletrodo pode ser dividida em dois processos:(a) uma mudança de forma devido à inserção de lítio e (b) uma deformação elástica reversível. Esses dois processos de deformação podem ser descritos por dois tensores de gradiente separados e o tensor de gradiente de deformação total pode ser escrito como
$$ \ mathbf {F} ={\ mathbf {F}} ^ e {\ mathbf {F}} ^ c $$ (4)
onde F ^e representa a deformação elástica, F ^c representa a mudança de forma devido à inserção de lítio. A equação (4) representa o processo do material do eletrodo do estado inicial (não deformado) ao estado atual (deformado). Assumindo que a mudança de forma devido à inserção de lítio é isotrópica, F ^c pode ser dado por
$$ {\ mathbf {F}} ^ c ={\ left (1+ \ Omega C \ right)} ^ {1/3} \ mathbf {I}, $$ (5)
onde Ω representa o volume molar parcial.

Da Eq. (3–5), o tensor gradiente de deformação elástica F ^e é
$$ {\ mathbf {F}} ^ e ={\ left (1+ \ Omega (R) C \ right)} ^ {- 1/3} \ left [\ begin {array} {ccc} 1+ \ parcial u / \ parcial R &0 &0 \\ {} 0 &1 + u / R &0 \\ {} 0 &0 &1 + u / R \ end {array} \ right]. $$ (6)
O tensor de deformação total de Green-Lagrange E pode ser escrito como
$$ \ mathbf {E} =\ frac {1} {2} \ left ({\ mathbf {F}} ^ T \ mathbf {F} - \ mathbf {I} \ right), $$ (7)
onde o tensor de deformação elástica E ^e e tensor de deformação induzida por difusão E ^c são
$$ {\ mathbf {E}} ^ e =\ frac {1} {2} \ left ({\ left ({\ mathbf {F}} ^ e \ right)} ^ T {\ mathbf {F}} ^ e- \ mathbf {I} \ right), {\ mathbf {E}} ^ c =\ frac {1} {2} \ left ({\ left ({\ mathbf {F}} ^ c \ right)} ^ T {\ mathbf {F}} ^ c- \ mathbf {I} \ right), $$ (8)
respectivamente.

Substituindo a Eq. (6) na Eq. (8), os componentes radiais e tangenciais do tensor de deformação Green-Lagrange são
$$ {E} _R ^ e =\ frac {1} {2} \ esquerda [\ frac {{\ esquerda (1+ \ parcial u / \ parcial R \ direita)} ^ 2} {{\ esquerda (1+ \ Omega (R) C \ direita)} ^ {2/3}} - 1 \ direita], $$ (9) $$ {E} _ {\ Theta} ^ e ={E} _ {\ Phi} ^ e =\ frac {1} {2} \ left [\ frac {{\ left (1 + u / R \ right)} ^ 2} {{\ left (1+ \ Omega (R) C \ right)} ^ {2/3}} - 1 \ direita]. $$ (10)
A relação constitutiva para a deformação pode ser determinada a partir da densidade de energia de deformação como
$$ \ mathbf {P} =\ frac {\ parcial W} {\ parcial \ mathbf {F}} =\ frac {\ parcial W} {\ parcial {\ mathbf {E}} ^ e} \ frac {\ parcial {\ mathbf {E}} ^ e} {\ parcial {\ mathbf {F}} ^ e} \ frac {\ parcial {\ mathbf {F}} ^ e} {\ partial \ mathbf {F}}, $$ (11)
onde W é a densidade de energia de deformação elástica na descrição Lagrangiana, e P é o primeiro estresse Piola-Kirchhoff. Além disso, se o material for linearmente elástico, W pode ser escrito como uma função quadrática do tensor de deformação Green-Lagrange
$$ W =\ frac {1} {2} {\ mathbf {E}} ^ e:\ mathbf {C}:{\ mathbf {E}} ^ e =\ det \ left ({\ mathbf {F}} ^ c \ direita) \ frac {E_h} {2 \ esquerda (1+ \ nu \ direita)} \ esquerda [\ frac {\ nu} {\ esquerda (1-2 \ nu \ direita)} {\ esquerda [tr \ left ({\ mathbf {E}} ^ e \ right) \ right]} ^ 2+ tr \ left ({\ mathbf {E}} ^ e {\ mathbf {E}} ^ e \ right) \ right] . $$ (12)
Aqui, E _h e ν são o módulo de Young e o coeficiente de Poisson, respectivamente, C é o tensor de rigidez, e det ( F ^c ) é o determinante do tensor de gradiente de deformação para a deformação induzida por difusão.

Finalmente, o primeiro estresse Piola-Kirchhoff é dado por
$$ \ mathbf {P} =\ det \ left ({\ mathbf {F}} ^ c \ right) \ frac {E_h} {\ left (1+ \ nu \ right)} \ left [\ frac {\ nu } {\ left (1-2 \ nu \ right)} tr \ left ({\ mathbf {E}} ^ e \ right) + {\ mathbf {E}} ^ e \ right] {\ mathbf {F}} ^ e {\ left ({\ mathbf {F}} ^ c \ right)} ^ {- 1}. $$ (13)
Combinando Eqs. (5), (9), (10) e (13), os componentes correspondentes do primeiro tensor de tensão Piola-Kirchhoff (P-K) são
$$ {P} _R ={\ left (1+ \ Omega C \ right)} ^ {1/3} \ frac {E_h} {2 \ left (1+ \ nu \ right) \ left (1-2 \ nu \ direita)} \ esquerda (1+ \ frac {\ parcial u} {\ parcial R} \ direita) \ esquerda [\ esquerda (1-v \ direita) {E} _R ^ e + 2 {vE} _ { \ Theta} ^ e \ right], $$ (14) $$ {P} _ {\ Theta} ={P} _ {\ Phi} ={\ left (1+ \ Omega C \ right)} ^ {1 / 3} \ frac {E_h} {2 \ left (1+ \ nu \ right) \ left (1-2 \ nu \ right)} \ left (1+ \ frac {u} {R} \ right) \ left ({vE} _R ^ e + {E} _ {\ Theta} ^ e \ direita), $$ (15)
E o primeiro estresse P-K deve satisfazer a condição de equilíbrio na ausência de força corporal
$$ \ frac {\ parcial {P} _R} {\ parcial R} +2 \ frac {P_R- {P} _ {\ Phi}} {R} =0, $$ (16)
com condições iniciais e de limite
$$ u \ left (0, \ mathrm {t} \ right) =0, {P} _R \ left ({\ mathrm {R}} _ 0, \ mathrm {t} \ right) =0. $$ (17)

Equação de transporte de massa

A concentração e o fluxo de difusão do lítio nos eletrodos, que são funções de coordenadas e tempo, serão denominados C ( X , T) e J ( X , T) na descrição Lagrangiana, e eles devem ser satisfeitos com a equação de transporte de massa escrita como
$$ \ frac {\ partial C} {\ partial t} + \ mathrm {Div} \ mathbf {J} =0, $$ (18)
onde Div representa o operador de divergência na descrição Lagrangiana. Considerando a característica de simetria esférica, a difusão ocorre apenas na direção radial e usamos J ( R , t) para representar o componente radial de J ( X , t). No sistema esférico, a Eq. (18) torna-se
$$ \ frac {\ parcial C \ esquerda (R, t \ direita)} {\ parcial t} + \ frac {\ parcial \ esquerda ({R} ^ 2J \ esquerda (R, t \ direita) \ direita)} {R ^ 2 \ R parcial} =0. $$ (19)
A difusão do lítio nos eletrodos é impulsionada pelo gradiente de potencial químico e pelo fluxo radial J ( R , t) é proporcional ao gradiente de potencial químico μ , como [11]
$$ J =- \ frac {CD} {R_g {TF} _ {11} {F} _ {11}} \ frac {\ parcial \ mu} {\ parcial R}, $$ (20)
onde D é a difusividade, R _g é a constante do gás, e T é a temperatura. μ é definido como o desvio da densidade total de energia para a concentração e pode ser escrito como
$$ \ mu =\ frac {\ mathrm {\ parcial \ Pi}} {\ parcial C}. $$ (21)
Suponha que a densidade de energia do sistema, Π, pode ser descrita como a soma da densidade de energia química e densidade de energia de deformação. Portanto, a densidade de energia interna total pode ser escrita como
$$ \ Pi \ left (\ mathbf {X}, \ mathrm {t} \ right) =\ varphi (C) + W \ left (C, {\ mathbf {E}} ^ e \ right). $$ (22)
Substituindo a Eq. (22) na Eq. (21), o potencial químico μ pode ser demonstrado que é
$$ \ mu =\ frac {\ mathrm {\ parcial \ Pi}} {\ parcial C} =\ frac {\ parcial \ varphi} {\ parcial C} + \ frac {\ parcial W} {\ parcial C} ={\ mu} _0 (C) + \ tau \ left ({\ mathbf {E}} ^ e, C \ right) $$ (23)
onde μ ₀ ( C ) e τ ( E ^e , C ) são as partes independentes e dependentes de tensão do potencial químico, respectivamente. E
$$ {\ mu} _0 (C) ={\ mu} _0 + {R} _gT \ ln \ left (\ gamma C \ right) $$ (24)
onde μ ₀ é uma constante que representa o potencial químico em um estado padrão, e γ é o coeficiente de atividade que representa os efeitos das interações entre os átomos / moléculas. Para uma solução diluída, as interações entre os átomos / moléculas são desprezíveis; assim, γ =1.

Nós nos concentramos na parte dependente do estresse do potencial químico τ ( E ^e , C), que é a derivada da densidade de energia de deformação W no que diz respeito à concentração de lítio C. Tradicionalmente, Π ( X , T) é considerada a densidade de energia livre de Helmholtz e, portanto, esta etapa é realizada para deformação fixa escrita como [11]
$$ {\ tau} _H \ left ({\ mathbf {E}} ^ e, \ mathrm {C} \ right) =\ frac {\ partial W} {\ partial C} \ left | \ begin {array} { c} \\ {} \ mathbf {F} \ end {array} \ right. =- \ det \ left ({\ mathbf {F}} ^ e \ right) {\ sigma} _m \ Omega. $$ (25)
O subscrito H significa que é causado pela densidade de energia livre de Helmholtz. O potencial químico acaba por ser
$$ \ mu ={\ mu} _0 + {R} _gT \ kern0.5em \ ln (C) - \ det \ left ({\ mathbf {F}} ^ e \ right) \ Omega {\ sigma} _m $$ (26)
onde σ _m é a tensão hidrostática de Cauchy na descrição euleriana e pode ser obtida por
$$ {\ boldsymbol {\ upsigma}} _ m =\ frac {1} {3} tr \ left (\ boldsymbol {\ upsigma} \ right) =\ frac {1} {3} tr \ left ({\ det} ^ {- 1} \ left (\ mathbf {F} \ right) {\ mathbf {PF}} ^ T \ right). $$ (27)
É importante notar que a rigidez C do material do eletrodo é considerado independente da concentração de lítio C na Eq. (12). Além disso, det ( F ^e ) ≈ 1 é amplamente aceito, de modo que geralmente é ignorado. No restante deste artigo, chamamos Eq. (26) como a expressão tradicional do potencial químico. Por outro lado, Π ( X , T) é considerada a densidade de energia livre de Gibbs em alguns estudos [12, 13] no modelo de campo de fase, de modo que não podemos obter uma expressão desenvolvida de τ ( E ^e , C), e
$$ {\ tau} _G \ left ({\ mathbf {E}} ^ e, \ mathrm {C} \ right) =\ frac {\ parcial W} {\ parcial C}. $$ (28)
O subscrito G significa que é causado pela densidade de energia livre de Gibbs. Nesse caso, μ torna-se
$$ \ mu ={\ mu} _0 + {R} _gT \ kern0.5em \ ln (C) - \ frac {\ parcial W} {\ parcial C} $$ (29)
e chamamos Eq. (29) como a expressão desenvolvida do potencial químico.

A equação do transporte de massa é composta pelas Eqs. (19), (20), (26) e (29) com expressões tradicionais e desenvolvidas de potencial químico. Na parte restante deste artigo, compararemos os efeitos dessas duas expressões de potencial químico na tensão induzida por difusão e na concentração de Li sob diferentes métodos de carregamento.

Em termodinâmica, a energia livre de Helmholtz é um potencial termodinâmico que mede o trabalho útil obtido a partir de um sistema termodinâmico fechado a uma temperatura e volume constantes. Em contraste, a energia livre de Gibbs mede o máximo de trabalho reversível que pode ser executado por um sistema termodinâmico a uma temperatura e pressão constantes. Em sólidos com baixo nível de tensão, a energia livre de Gibbs é aproximadamente equivalente à energia livre de Helmholtz, pois a deformação dos sólidos geralmente é pequena. Esta suposição é adequada para a maioria dos materiais sólidos devido à sua pequena deformação induzida pela difusão, mas exceto para o silício devido à sua grande expansão volumétrica durante a litiação. Na verdade, a difusão e a deformação ocorrem ao mesmo tempo, de modo que não é adequado assumir que não há deformação acontecendo enquanto a concentração está mudando. Mesmo assim, como pode ser visto na Eq. (25), a expressão tradicional do potencial químico ainda é precisa quando a taxa de deformação é baixa o suficiente. No entanto, é provável que cause grandes erros quando um eletrodo de nanopartícula de Si é litiado rapidamente.

O eletrodo é litiado com uma concentração constante de íons de lítio em sua superfície, ou seja, a operação potenciostática, ou com um fluxo constante em sua superfície, ou seja, a operação galvanostática. As condições de contorno da Eq. (19) são
$$ C \ left ({R} _0, \ mathrm {t} \ right) ={C} _ {\ mathrm {max}}, \ kern0.5em \ mathrm {para} \ \ mathrm {t} \ ge 0 , $$ (30) $$ J \ left ({R} _0, \ mathrm {t} \ right) ={j} _0 {\ left (1 + u / R \ right)} ^ 2, \ kern0,5em \ mathrm {para} \ \ mathrm {t} \ ge 0, $$ (31)
respectivamente. A condição inicial é escrita como
$$ C \ left (R, 0 \ right) =0 \ \ mathrm {para} \ 0 \ le R \ le {R} _0, $$ (32)
para cada operação de carga. Aqui, C _máximo é a concentração máxima de lítio do material e j ₀ é uma constante que representa a corrente de carga.

Implementação Numérica

É muito difícil obter a solução analítica do sistema acima consistindo em equações diferenciais parciais, senão impossível. Com Eqs. (1) - (3) e (13) - (18), calculamos a evolução do estresse induzido pela difusão e da concentração de lítio numericamente usando o software COMSOL multifísica. É estudada a litiação de um nanoeletrodo de silício sob operações potenciostáticas e galvanostáticas, com diferentes expressões de potencial químico. As propriedades do material de Si e os parâmetros operacionais usados na simulação estão listados na Tabela 1. Por conveniência, a substituição adimensional correspondente de coordenada, tensão e concentração são usados nas figuras.

Para investigar a diferença entre as diferentes expressões de potencial químico em diferentes momentos no eletrodo esférico de Si, o estado de carga (SOC) é calculado como
$$ SOC =\ frac {\ int_0 ^ {R_0} C \ left (R, t \ right) {R} ^ 2 dR} {\ int_0 ^ {R_0} {C} _ {\ mathrm {max}} {R } ^ 2 dR}. $$ (33)
Os fluxos de difusão induzidos por tensão na descrição Lagrangiana são descritos como
$$ {J} _H =\ frac {\ partial {\ tau} _H \ left ({\ mathbf {E}} ^ e, C \ right)} {\ partial R}, {J} _G =\ frac {\ parcial {\ tau} _G \ left ({\ mathbf {E}} ^ e, C \ right)} {\ partial R}, $$ (34)
representando o fluxo causado por diferentes expressões de potenciais químicos, respectivamente.

Resultados e discussão

A Figura 1 mostra a distribuição espacial da concentração de lítio, tensão radial e tensão circular em um eletrodo esférico de Si sob operação galvanostática em vários SOCs. Para efeito de comparação, os resultados numéricos com as expressões desenvolvidas e tradicionais de potencial químico são incluídos e são representados por linhas sólidas e símbolos de triângulos, respectivamente. Para cada SOC na Fig. 1a, a linha sólida quase se sobrepõe aos símbolos do triângulo. O efeito causado pelas diferentes expressões do potencial químico na concentração de lítio pode ser ignorado. Na Fig. 1b e na Fig. 1c, para os SOCs de 46,7% e 65,5%, as linhas sólidas são mais altas do que os triângulos no centro, enquanto quase se sobrepõem do lado de fora, assim como em outros SOCs. Em geral, há um ligeiro efeito na concentração de lítio e nas tensões sob operação galvanostática. A Figura 2 mostra as distribuições espaciais da concentração de lítio, tensão radial e tensão circular em um eletrodo esférico de Si sob operação potenciostática em vários SOCs. É importante mencionar que as tensões radial e circular primeiro aumentam e depois diminuem com o aumento do SOC tanto na Fig. 1 quanto na Fig. 2. É porque o eletrodo de silício no estado inicial ou totalmente litiado é livre de tensões, uma vez que não há gradiente de concentração. Em comparação com a Fig. 1a, a diferença entre linhas sólidas e triângulos é maior na Fig. 2a. Devido à concentração de lítio na superfície é uma constante C _máximo sob operação potenciostática, a taxa de carga é maior do que a taxa de deformação da operação galvanostática e a taxa de deformação também. No entanto, a deformação total sob o mesmo SOC é quase a mesma, independentemente do método de carga, apenas levando um tempo diferente. Isso indica que a influência na distribuição do lítio causada por diferentes expressões de potencial químico está relacionada apenas à taxa de deformação e não à deformação e aumenta com o aumento da taxa de deformação. Na verdade, os experimentos existentes mostram que os eletrodos de silício se deformam muito rapidamente durante a litiação em certos modos de carregamento. Como podemos ver na Fig. 3 [17], o ânodo de Si é totalmente deformado em 1 min com um potencial de 2 V em relação ao metal Li. Nessa condição, os resultados resolvidos por essas duas expressões de potencial químico serão significativamente diferentes. Infelizmente, neste caso, a tensão do eletrodo não pode ser medida com precisão e, portanto, não pode ser comparada quantitativamente com nosso modelo.

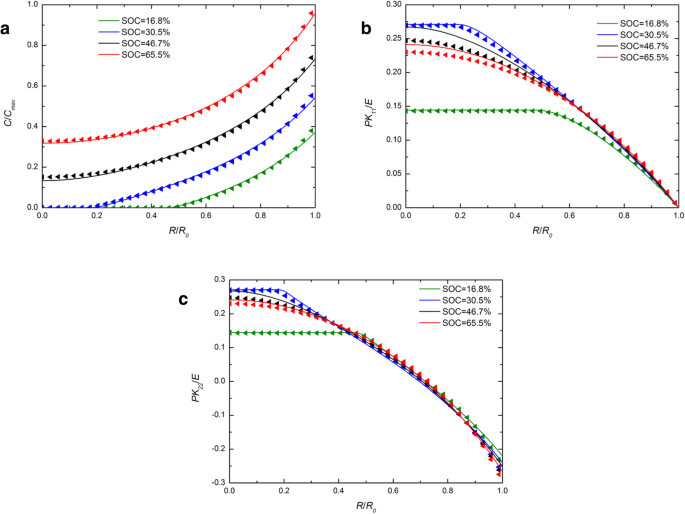
Distribuição espacial de ( a ) a concentração de lítio, ( b ) tensão radial, e ( c ) tensão circular em um eletrodo esférico de Si em diferentes SOCs sob operação galvanostática (as linhas sólidas representam os resultados com a expressão tradicional do potencial químico; as linhas dos triângulos representam os resultados com a expressão desenvolvida do potencial químico)

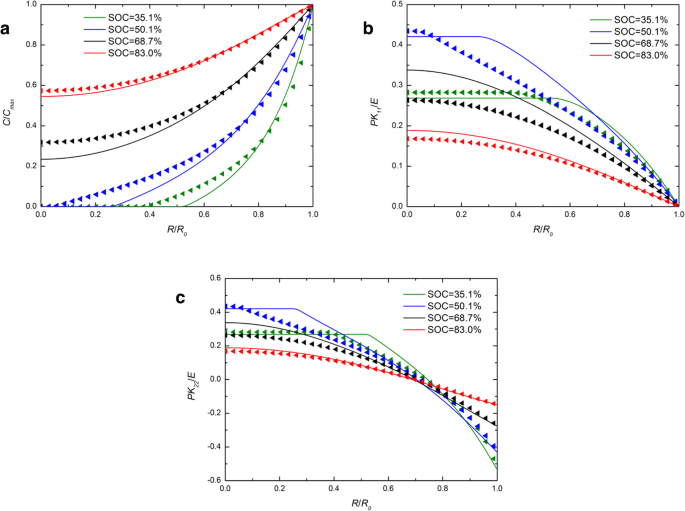
Distribuição espacial de ( a ) a concentração de lítio, ( b ) tensão radial, e ( c ) tensão circular em um eletrodo esférico de nanopartículas de Si em diferentes SOCs sob operação potenciostática (as linhas sólidas representam os resultados com a expressão tradicional do potencial químico; as linhas dos triângulos representam os resultados com a expressão desenvolvida do potencial químico)

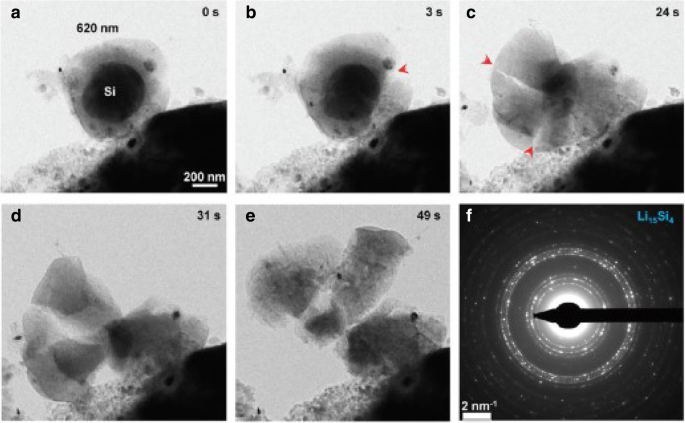
Deformação rápida de um SiNP autônomo de 620 nm durante a litiação química em 1 min. a - e Sequência de tempo de início e crescimento da fissura. f EDP indicando a formação de Li policristalino ₁₅ Si ₄ como a fase totalmente litiada

A Figura 4 mostra a distribuição espacial de J _H / J _G em um eletrodo esférico de Si em diferentes SOCs sob operação galvanostática com diferentes j . Na Fig. 4, as linhas sólidas quase coincidem com os triângulos, o que indica que diferentes expressões de potencial químico têm um leve efeito na proporção de J _H e J _G . É evidente que o intervalo dos valores de J _H / J _G aumenta com o aumento da corrente de carga. Isso ocorre porque a maior corrente de carga leva a maiores taxas de deformação e, portanto, causando o maior impacto de diferentes expressões de potencial químico. A proporção é sempre maior que 1 no centro e menor que 1 na superfície. Isso sugere que o fluxo obtido a partir da expressão desenvolvida do potencial químico na superfície é maior do que o obtido na expressão tradicional, enquanto o oposto é verdadeiro no centro. Notamos que todas as linhas sólidas e triângulos na Fig. 4 quase se cruzam com um ponto. Além disso, a razão correspondente à interseção é sempre cerca de 1, não importa com qual corrente o eletrodo está carregado. Isso sugere que existe um raio crítico onde o fluxo é menos afetado pelas diferentes expressões de potencial químico. Nós a chamamos de região independente do potencial químico (CIR). Obviamente, CIR está sempre perto da superfície do eletrodo esférico e está mais perto da superfície conforme a corrente de carga aumenta.

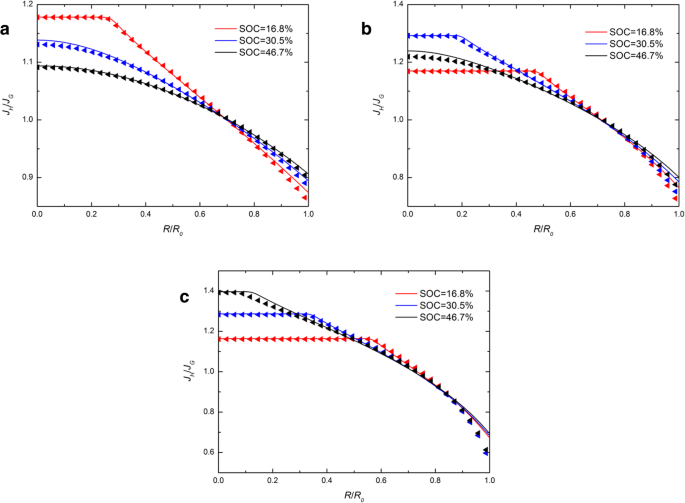
Distribuição espacial de J _H / J _G em um eletrodo esférico de nanopartículas de Si em diferentes SOCs sob operação galvanostática com ( a ) j =0,5 j ₀ , ( b ) j = j ₀ , e ( c ) j =1,5 j ₀ (as linhas sólidas representam os resultados com a expressão tradicional do potencial químico; as linhas dos triângulos representam os resultados com a expressão desenvolvida do potencial químico)

Ao comparar os potenciais químicos tradicionais e desenvolvidos na Eq. (26) e Eq. (29), verifica-se que a tensão hidrostática de Cauchy σ _m é a chave para a diferença entre essas duas expressões. A fim de investigar as causas do CIR, a distribuição espacial de σ _m / E em um eletrodo esférico de Si em diferentes SOCs sob operação galvanostática com diferentes expressões de potencial químico são dados na Fig. 5 e na Fig. 6. Obviamente, quase todas as curvas se cruzam em um ponto em CIR e a tensão hidrostática de Cauchy σ _m é próximo de 0 neste ponto, exceto no início do carregamento (SOC =6,2%). Isso indica que σ _m em CIR é mantido em um nível baixo (quase 0) durante a maior parte do período de carga. Pode ser interpretado que as duas expressões de potencial químico são quase equivalentes quando a tensão hidrostática σ _m está próximo de 0. Isso pode explicar parcialmente por que CIR aparece, mas não é suficiente para explicar as características das curvas em σ _m . Isso precisa ser resolvido em nossa próxima pesquisa.

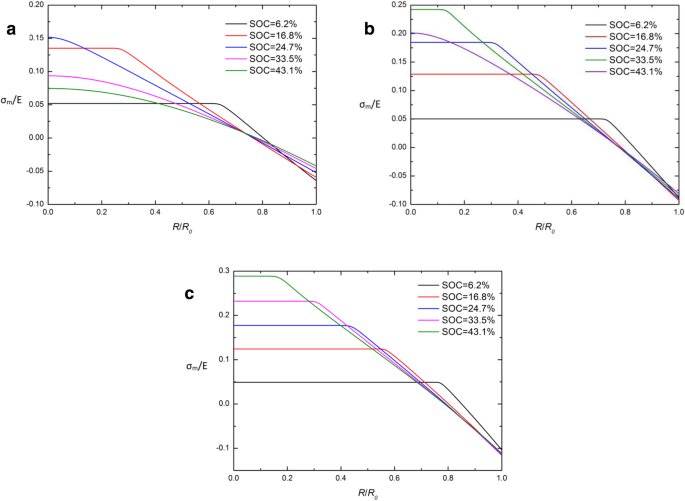
Distribuição espacial de σ _m / E em um eletrodo esférico de nanopartículas de Si em diferentes SOCs sob operação galvanostática com a expressão tradicional de potencial químico e ( a ) j =0,5 j ₀ , ( b ) j = j _0, e ( c ) j =1,5 j ₀

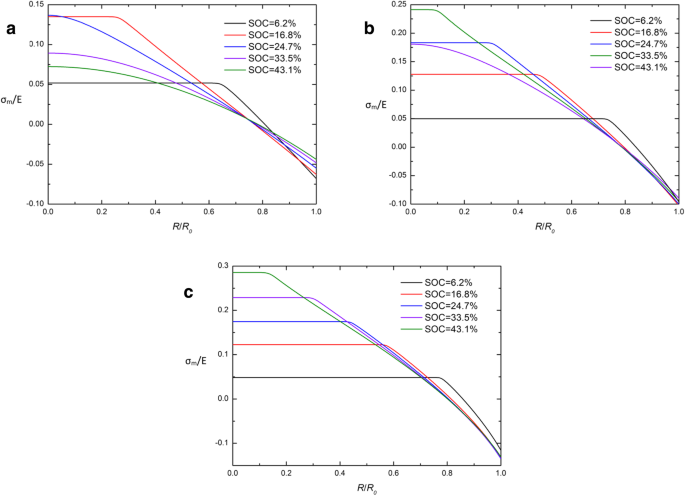
Distribuição espacial de σ _m / E em um eletrodo esférico de nanopartículas de Si em diferentes SOCs sob operação galvanostática com a expressão desenvolvida de potencial químico ( a ) j =0,5 j ₀ , ( b ) j = j ₀ , e ( c ) j =1,5 j ₀ s

Conclusões

Neste trabalho, uma expressão desenvolvida de potencial químico é proposta sem a suposição de baixa taxa de deformação, distinta da expressão desenvolvida que é amplamente utilizada na atualidade. A diferença entre as expressões tradicionais e desenvolvidas de potencial químico nas distribuições de estresse e concentração em eletrodos de nanopartículas de Si é discutida em operações potenciostáticas e galvanostáticas.

O resultado revela que o efeito causado por diferentes expressões de potencial químico pode ser desprezado na operação galvanostática, mas é significativo na operação potenciostática. Verifica-se que o efeito está relacionado apenas à taxa de deformação e não à deformação, podendo ser maior com o aumento da taxa de deformação. Considerando a suposição de baixa taxa de deformação na expressão do potencial químico tradicional, acredita-se que os resultados obtidos pela expressão do potencial químico desenvolvido sejam mais confiáveis. Uma região independente de potencial químico (CIR), onde o fluxo causado pelo potencial químico tradicional e desenvolvido é quase o mesmo durante a maior parte do processo litiado, é encontrada perto da superfície do eletrodo de nanopartículas. Além disso, o CIR está mais próximo da superfície com o aumento da corrente de carga. Um fenômeno semelhante também aparece nas curvas de tensão hidrostática de Cauchy. A tensão hidrostática de Cauchy σ _m mantém uma constante e mantida em um nível baixo (quase 0) em CIR na maioria das vezes, não importa qual expressão de potencial químico é usada. Tais resultados ainda não foram relatados na literatura.

Disponibilidade de dados e materiais

Os conjuntos de dados analisados durante o estudo atual estão disponíveis com o autor correspondente mediante solicitação razoável.

Abreviações

CIR:: Uma região onde o fluxo de difusão causado por essas duas expressões de potencial químico é quase o mesmo

Mini revisão sobre eletrônicos flexíveis e vestíveis para monitorar informações de saúde humana Transporte aprimorado de elétrons da interface do cátodo PF-NR2 por nanopartículas de ouro

Nanomateriais

Materiais Poliméricos

biológico

Corante

Especiarias