Convertendo tabelas da verdade em expressões booleanas

Ao projetar circuitos digitais, o projetista geralmente começa com uma tabela de verdade que descreve o que o circuito deve fazer.

A tarefa do projeto consiste principalmente em determinar que tipo de circuito executará a função descrita na tabela verdade.

Embora algumas pessoas pareçam ter uma habilidade natural de olhar para uma tabela verdade e imaginar imediatamente a porta lógica ou circuito lógico de relé necessários para a tarefa, existem técnicas de procedimento disponíveis para o restante de nós.

Aqui, a álgebra booleana prova sua utilidade da maneira mais dramática.

Para ilustrar esse método procedimental, devemos começar com um problema de projeto realista.

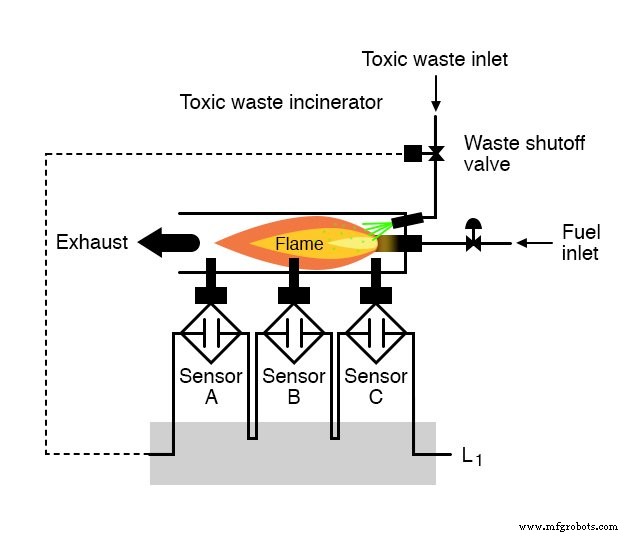
Suponha que recebamos a tarefa de projetar um circuito de detecção de chama para um incinerador de lixo tóxico.

O intenso calor do incêndio tem como objetivo neutralizar a toxicidade dos resíduos introduzidos no incinerador.

Essas técnicas baseadas em combustão são comumente usadas para neutralizar resíduos médicos, que podem estar infectados com vírus ou bactérias mortais:







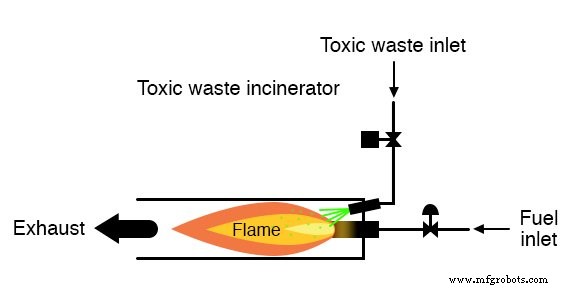
Enquanto a chama for mantida no incinerador, é seguro injetar resíduos nele para serem neutralizados.

Se a chama fosse extinta, no entanto, não seria seguro continuar a injetar resíduos na câmara de combustão, uma vez que sairia do escapamento sem neutralização e representaria uma ameaça à saúde para qualquer pessoa nas proximidades do escapamento.

O que precisamos neste sistema é uma maneira segura de detectar a presença de uma chama e permitir que os resíduos sejam injetados apenas se a chama for “comprovada” pelo sistema de detecção de chama.

Existem várias tecnologias diferentes de detecção de chama:óptica (detecção de luz), térmica (detecção de alta temperatura) e condução elétrica (detecção de partículas ionizadas no caminho da chama), cada uma com suas vantagens e desvantagens exclusivas.

Suponha que, devido ao alto grau de risco envolvido com a passagem potencial de resíduos não neutralizados para fora da exaustão deste incinerador, seja decidido que o sistema de detecção de chama seja redundante (sensores múltiplos), de modo que a falha de um único sensor não conduza a uma emissão de toxinas pelo escapamento.

Cada sensor vem equipado com um contato normalmente aberto (aberto se não houver chama, fechado se houver chama detectada) que usaremos para ativar as entradas de um sistema lógico:







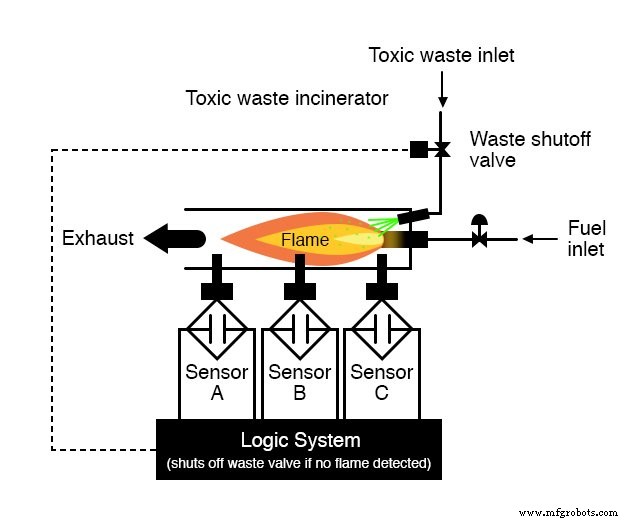
Nossa tarefa, agora, é projetar o circuito do sistema lógico para abrir a válvula de resíduos se e somente se houver boa chama comprovada pelos sensores.

Porém, primeiro devemos decidir qual deve ser o comportamento lógico desse sistema de controle.

Queremos que a válvula seja aberta se apenas um dos três sensores detectar chama? Provavelmente não, porque isso anularia o propósito de ter vários sensores.

Se qualquer um dos sensores falhasse de forma a indicar falsamente a presença de chama quando não havia nenhuma, um sistema lógico baseado no princípio de "qualquer um dos três sensores mostrando chama" daria a mesma saída que um sistema de sensor único teria a mesma falha.

Uma solução muito melhor seria projetar o sistema de forma que a válvula seja comandada para abrir se e somente se todos os três sensores detectar uma boa chama.

Dessa forma, qualquer sensor único com falha que mostre falsamente a chama não poderia manter a válvula na posição aberta; em vez disso, seria necessário que todos os três sensores falhassem da mesma maneira - um cenário altamente improvável - para que essa condição perigosa ocorresse.

Assim, nossa tabela de verdade ficaria assim:







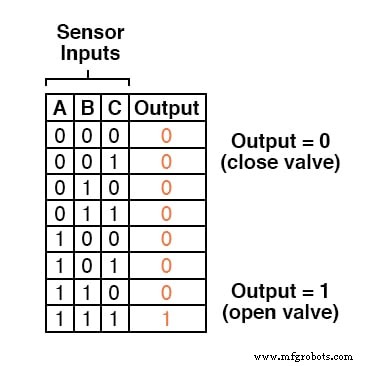
Não é necessário muito conhecimento para perceber que essa funcionalidade poderia ser gerada com uma porta AND de três entradas:a saída do circuito será "alta" se e somente se a entrada A E insira B E entrada C são todas “altas:”







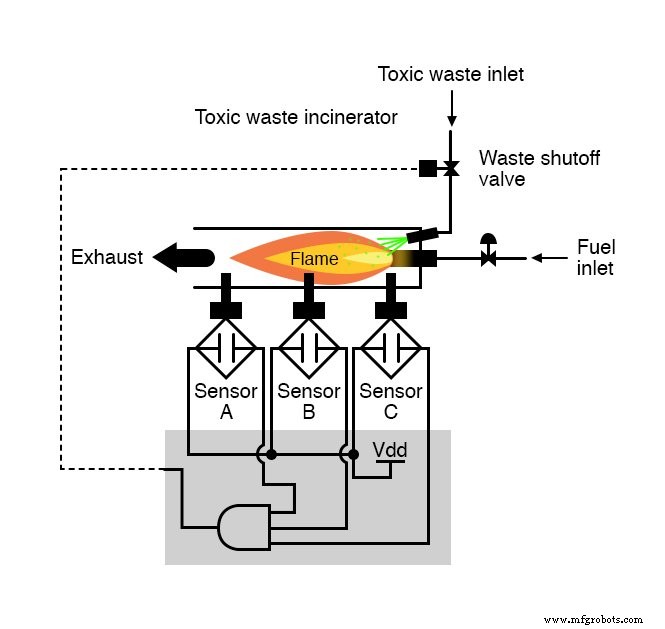
Se usarmos circuitos de relé, poderíamos criar esta função AND ligando três contatos de relé em série ou simplesmente ligando os três contatos de sensor em série, de modo que a única maneira de enviar energia elétrica para abrir a válvula de desperdício é se todos os três sensores indicar chama:







Embora essa estratégia de projeto maximize a segurança, ela torna o sistema muito suscetível a falhas de sensor do tipo oposto.

Suponha que um dos três sensores falhe de tal forma que não indique nenhuma chama quando realmente havia uma boa chama na câmara de combustão do incinerador.

Essa única falha desligaria a válvula de resíduos desnecessariamente, resultando em perda de tempo de produção e desperdício de combustível (alimentando um incêndio que não estava sendo usado para incinerar resíduos).

Seria bom ter um sistema lógico que permitisse esse tipo de falha sem desligar o sistema desnecessariamente, mas ainda fornecesse redundância de sensor para manter a segurança no caso de um único sensor falhar "alto" (mostrando chama o tempo todo , se havia ou não um para detectar).

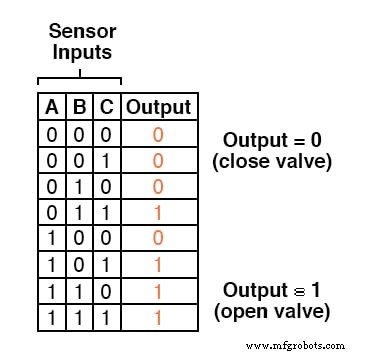
Uma estratégia que atendesse a ambas as necessidades seria uma lógica de sensor “dois em três”, em que a válvula de resíduos é aberta se pelo menos dois dos três sensores mostrarem boa chama.

A tabela verdade para tal sistema seria assim:

Usando Soma de Produtos

Aqui, não é necessariamente óbvio que tipo de circuito lógico satisfaria a tabela verdade.

No entanto, um método simples para projetar tal circuito é encontrado em uma forma padrão de expressão booleana chamada de Soma de Produtos , ou SOP , Formato.

Como você pode suspeitar, uma expressão booleana de soma de produtos é literalmente um conjunto de termos booleanos adicionados ( somados ) juntos, cada termo sendo um multiplicativo ( produto ) combinação de variáveis ​​booleanas.

Um exemplo de uma expressão SOP seria algo assim:ABC + BC + DF, a soma dos produtos “ABC,” “BC” e “DF”.

As expressões de soma de produtos são fáceis de gerar a partir de tabelas de verdade.

Tudo o que temos a fazer é examinar a tabela verdade para quaisquer linhas onde a saída é “alta” (1) e escrever um termo de produto booleano que seria igual a um valor de 1 dadas as condições de entrada.

Por exemplo, na quarta linha abaixo na tabela verdade para nosso sistema lógico dois de três, onde A =0, B =1 e C =1, o termo do produto seria A'BC, uma vez que esse termo teria um valor de 1 se e somente se A =0, B =1 e C =1:







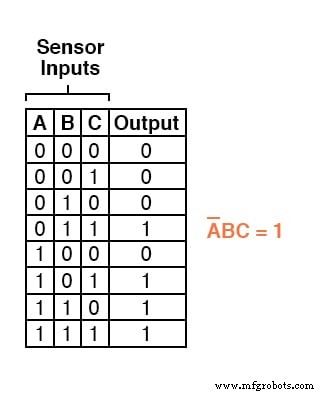
Três outras linhas da tabela verdade têm um valor de saída de 1, portanto, essas linhas também precisam de expressões de produto booleanas para representá-las:







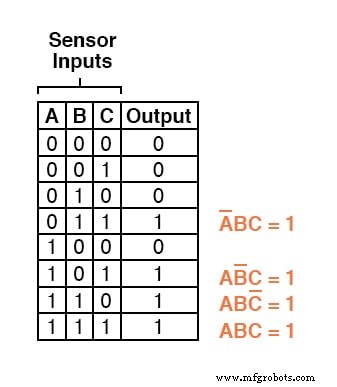
Finalmente, juntamos essas quatro expressões de produto booleanas por adição, para criar uma única expressão booleana que descreve a tabela verdade como um todo:







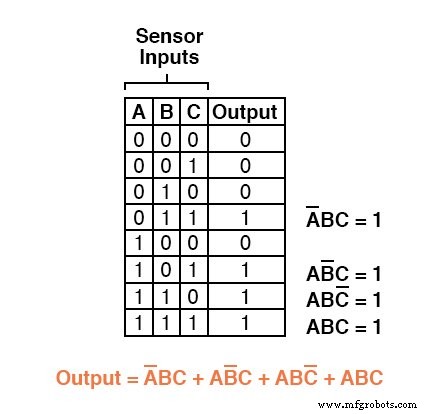
Agora que temos uma expressão Booleana Soma de Produtos para a função da tabela verdade, podemos facilmente projetar uma porta lógica ou circuito lógico de relé com base nessa expressão:











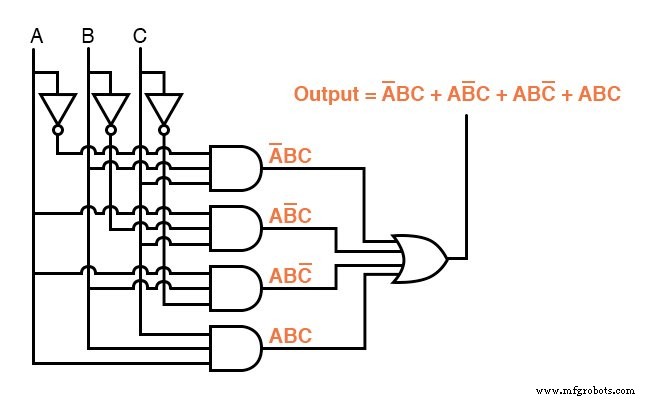
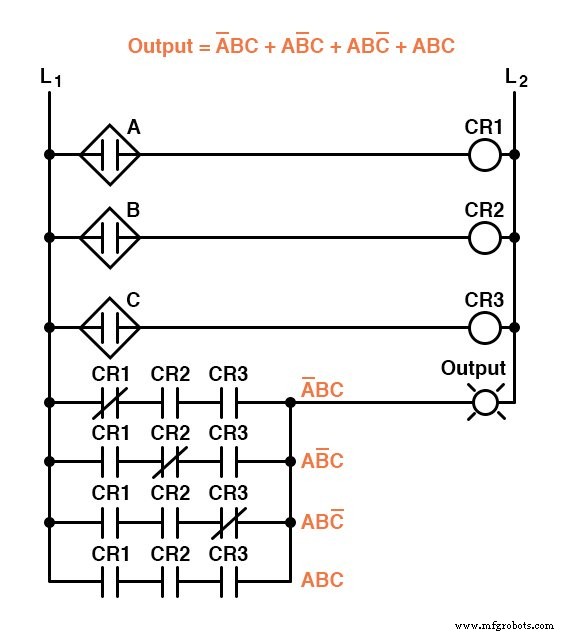
Infelizmente, esses dois circuitos são bastante complexos e poderiam se beneficiar com a simplificação.

Usando técnicas de álgebra booleana, a expressão pode ser significativamente simplificada:









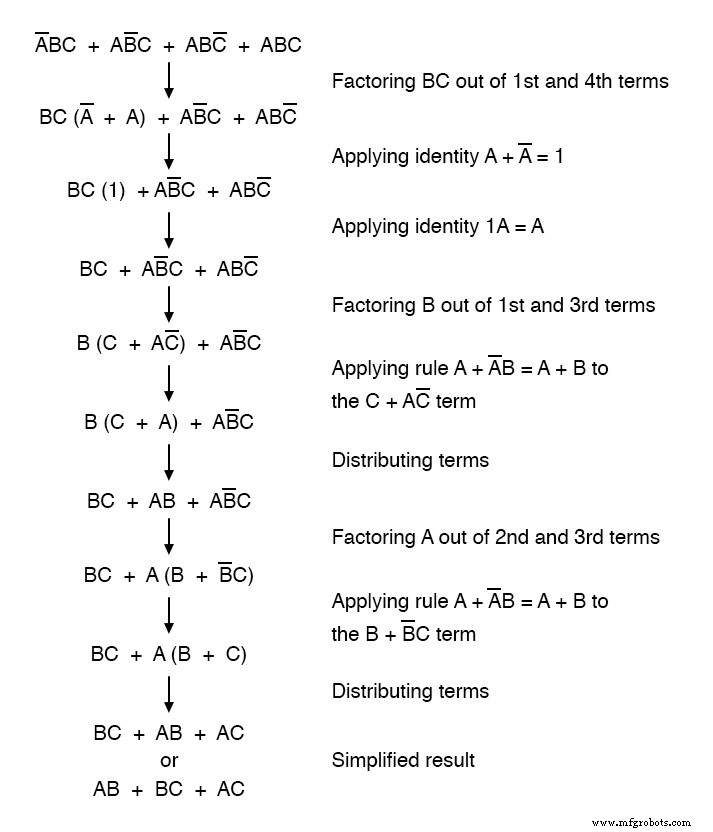
Como resultado da simplificação, podemos agora construir circuitos lógicos muito mais simples desempenhando a mesma função, tanto na forma de porta quanto de relé:









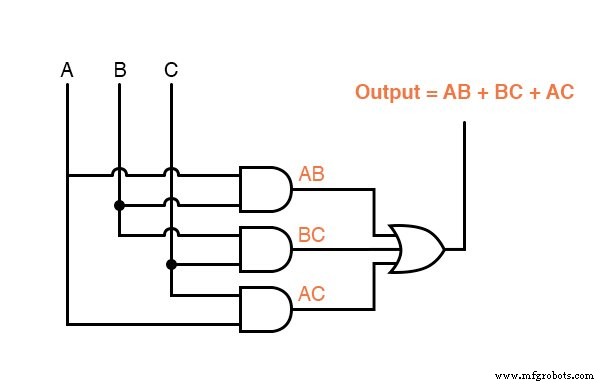
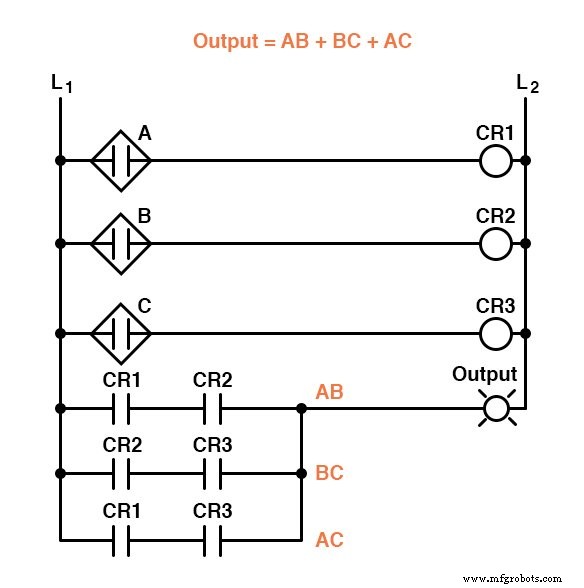
Qualquer um desses circuitos executará adequadamente a tarefa de operar a válvula de resíduos do incinerador com base em uma verificação de chama de dois dos três sensores de chama.

No mínimo, é disso que precisamos para ter um sistema incinerador seguro.

Podemos, no entanto, estender a funcionalidade do sistema adicionando a ele circuitos lógicos projetados para detectar se algum dos sensores não concorda com os outros dois.

Se todos os três sensores estiverem operando corretamente, eles devem detectar a chama com a mesma precisão.

Assim, eles devem registrar todos “baixo” (000:sem chama) ou todos registrar “alto” (111:chama boa).

Qualquer outra combinação de saída (001, 010, 011, 100, 101 ou 110) constitui uma discordância entre os sensores e pode, portanto, servir como um indicador de uma falha potencial do sensor.

Se adicionarmos circuitos para detectar qualquer uma das seis condições de “desacordo do sensor”, poderíamos usar a saída desse circuito para ativar um alarme.

Quem quer que esteja monitorando o incinerador, então, exercerá o julgamento em continuar a operar com um possível sensor com falha (entradas:011, 101 ou 110) ou desligar o incinerador para estar absolutamente seguro.

Além disso, se o incinerador for desligado (sem chama) e um ou mais dos sensores ainda indicar chama (001, 010, 011, 100, 101 ou 110) enquanto o (s) outro (s) indicam (m) nenhuma chama, será sabido que existe um problema definido no sensor.

A primeira etapa no projeto deste circuito de detecção de “desacordo de sensor” é escrever uma tabela verdade descrevendo seu comportamento.

Como já temos uma tabela verdade que descreve a saída do circuito lógico de “boa chama”, podemos simplesmente adicionar outra coluna de saída à tabela para representar o segundo circuito e fazer uma tabela que representa todo o sistema lógico:







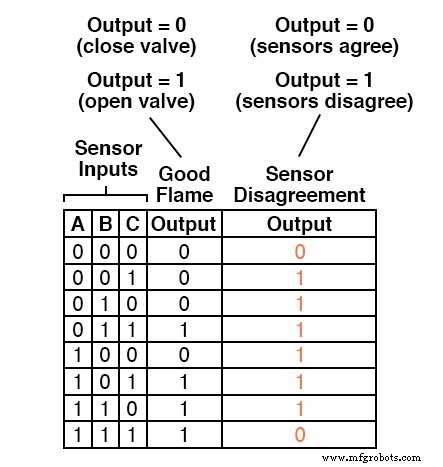
Embora seja possível gerar uma expressão de Soma de Produtos para esta nova coluna da tabela verdade, isso exigiria seis termos, de três variáveis ​​cada!

Essa expressão booleana exigiria muitas etapas para simplificar, com um grande potencial para cometer erros algébricos:

Usando Produto das somas

Uma alternativa para gerar uma expressão Soma-de-produtos para contabilizar todas as condições de saída “altas” (1) na tabela verdade é gerar um Produto-das-somas ou POS , expressão, para contabilizar todas as condições de saída “baixas” (0).

Sendo que há muito menos instâncias de uma saída “baixa” na última coluna da tabela verdade, a expressão Produto-das-somas resultante deve conter menos termos.

Como o próprio nome sugere, uma expressão Product-Of-Sums é um conjunto de termos adicionados ( somas ), que são multiplicados ( produto ) juntos.

Um exemplo de expressão POS seria (A + B) (C + D), o produto das somas “A + B” e “C + D”.

Para começar, identificamos quais linhas na última coluna da tabela verdade têm saídas "baixas" (0) e escrevemos um termo de soma booleana que seria igual a 0 para as condições de entrada dessa linha.

Por exemplo, na primeira linha da tabela verdade, onde A =0, B =0 e C =0, o termo da soma seria (A + B + C), já que esse termo teria um valor de 0 se e apenas se A =0, B =0 e C =0:







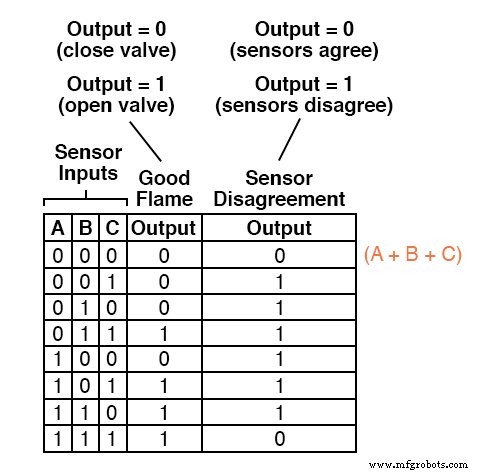
Apenas uma outra linha na última coluna da tabela verdade tem uma saída “baixa” (0), então tudo que precisamos é mais um termo de soma para completar nossa expressão Produto das somas.

Este último termo de soma representa uma saída 0 para uma condição de entrada de A =1, B =1 e C =1.

Portanto, o termo deve ser escrito como (A ’+ B’ + C ’), porque apenas a soma do complementado variáveis ​​de entrada seriam iguais a 0 apenas para essa condição:







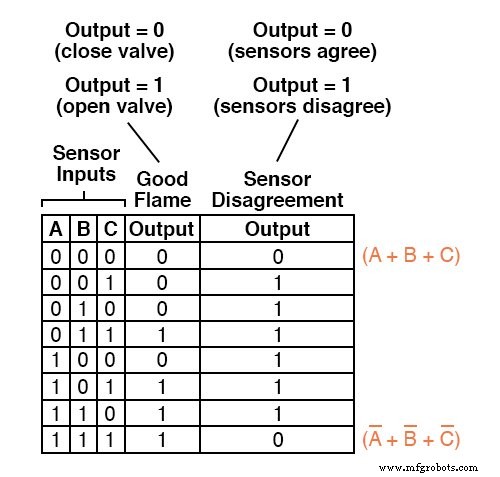
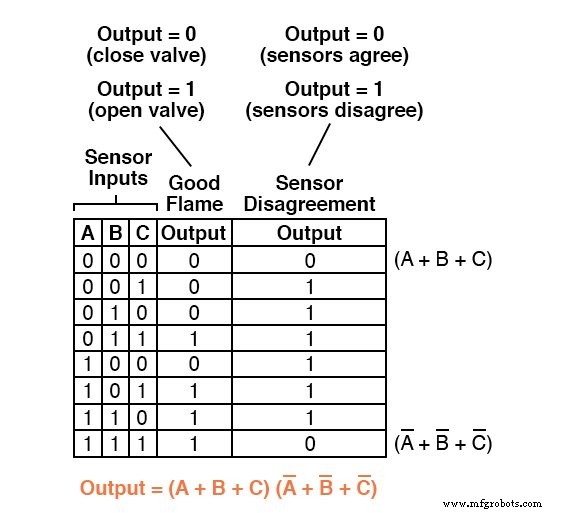
A expressão Product-Of-Sums completa, é claro, é a combinação multiplicativa desses dois termos de soma:







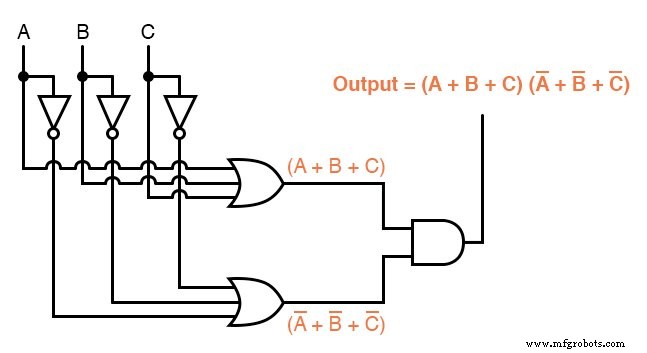
Enquanto uma expressão de Soma de Produtos pode ser implementada na forma de um conjunto de portas AND com suas saídas conectando-se a uma única porta OR, uma expressão de Produto de Soma pode ser implementada como um conjunto de portas OR alimentadas em um único E portão:









Correspondentemente, enquanto uma expressão de soma de produtos pode ser implementada como uma coleção paralela de contatos de relé conectados em série, uma expressão de produto de somas pode ser implementada como uma coleção em série de contatos de relé conectados em paralelo:







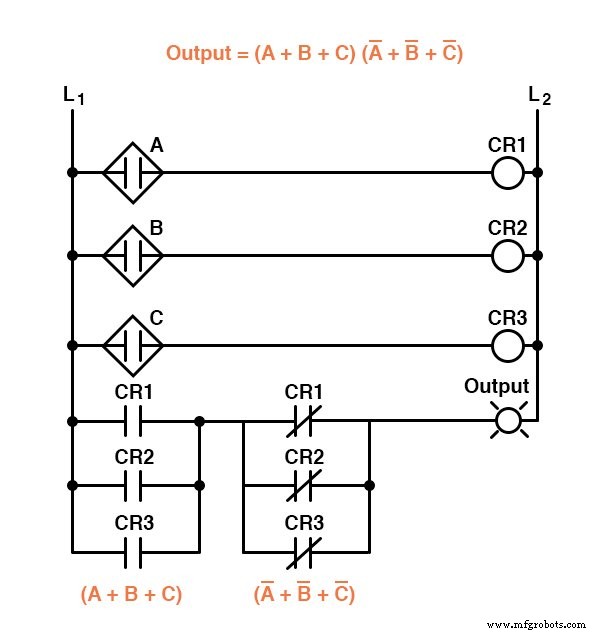
Os dois circuitos anteriores representam versões diferentes do circuito lógico de “desacordo do sensor” apenas, não o (s) circuito (s) de detecção de “chama boa”.

Todo o sistema lógico seria a combinação dos circuitos de “boa chama” e de “desacordo do sensor”, mostrados no mesmo diagrama.

Implementado em um controlador lógico programável (PLC), todo o sistema lógico pode se parecer com algo assim:







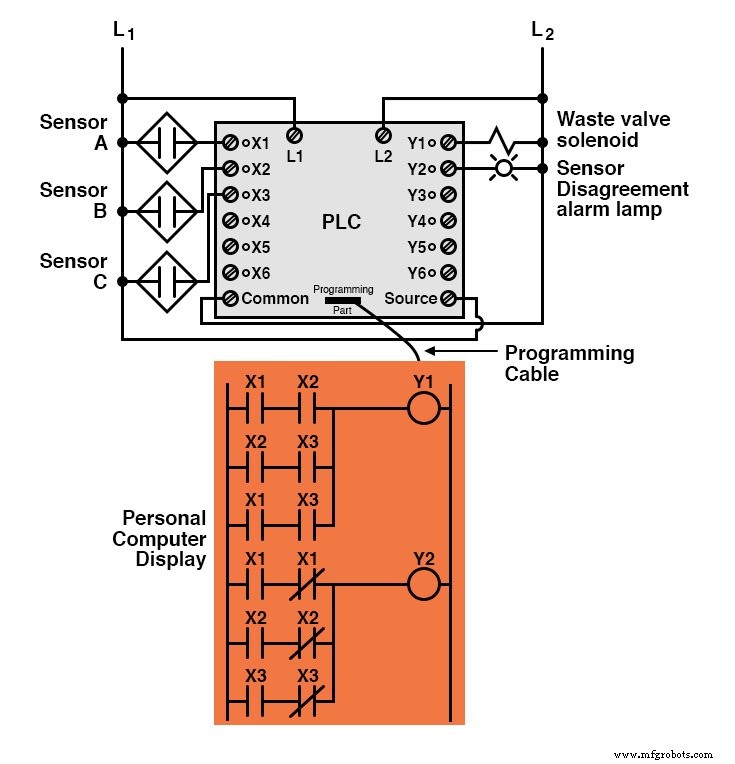
Como você pode ver, os formulários booleanos padrão Soma-Of-Products e Products-Of-Sums são ferramentas poderosas quando aplicadas a tabelas verdade.

Eles nos permitem derivar uma expressão booleana - e, em última análise, um circuito lógico real - de nada além de uma tabela verdade, que é uma especificação escrita para o que queremos que um circuito lógico faça.

Ser capaz de ir de uma especificação escrita a um circuito real usando procedimentos simples e determinísticos significa que é possível automatizar o processo de projeto de um circuito digital.

Em outras palavras, um computador poderia ser programado para projetar um circuito lógico personalizado a partir de uma especificação de tabela verdade!

Os passos a seguir de uma tabela de verdade para o circuito final são tão inequívocos e diretos que requer pouca ou nenhuma criatividade ou outro pensamento original para executá-los.



REVER:

• Soma de produtos , ou SOP , Expressões booleanas podem ser geradas a partir de tabelas verdade com bastante facilidade, determinando quais linhas da tabela têm uma saída de 1, escrevendo um termo de produto para cada linha e, finalmente, somando todos os termos de produto. Isso cria uma expressão booleana que representa a tabela verdade como um todo.
• Expressões de soma de produtos se prestam bem à implementação como um conjunto de portas AND (produtos) alimentando uma única porta OR (soma).
• Produto das somas ou POS , Expressões booleanas também podem ser geradas a partir de tabelas verdade com bastante facilidade, determinando quais linhas da tabela têm uma saída de 0, escrevendo um termo de soma para cada linha e, finalmente, multiplicando todos os termos de soma. Isso cria uma expressão booleana que representa a tabela verdade como um todo.
• Expressões de produto de somas se prestam bem à implementação como um conjunto de portas OR (somas) alimentadas em uma única porta AND (produto).

PLANILHAS RELACIONADAS:

• Planilha de expressões de soma de produtos e produto de somas
• Planilha de álgebra booleana