Confinamento aprimorado de polaritons de plasma de superfície Terahertz em guias de onda de metal semimetal-isolador de Dirac a granel

Resumo

Um guia de onda plasmonic terahertz de comprimento de onda baseado na estrutura de metal semimetal (BDS) -insulator (BIM) Dirac em massa é investigado, o que indica que há uma faixa de frequência otimizada com o melhor confinamento, bem como menor perda. Um confinamento de modo de banda larga até λ ₀ / 15 com uma perda relativamente baixa de 1,0 dB / λ ₀ pode ser conseguida. Também mostramos que duas fitas de silício introduzidas no guia de onda BIM podem formar um filtro sintonizável dinamicamente que adapta polaritons de plasmon de superfície terahertz em escala de sub-comprimento de onda profunda, que pode ser explorada posteriormente para o projeto de dispositivos plasmônicos THz ultracompactos com sintonia dinâmica. Nossos resultados também podem fornecer aplicações potenciais em filtragem óptica.

Histórico

A onda Terahertz (THz) tem sido extremamente testemunhada nas últimas décadas por suas aplicações inovadoras, como imagens THz, sensoriamento bioquímico e comunicações [1,2,3]. Para melhorar a sensibilidade de detecção, resolução de imagem e nível de integração de dispositivos THz, confinar a onda THz em uma escala profunda de comprimento de onda é urgentemente desejado [4,5,6]. Polaritons de plasmon de superfície (SPPs), os modos eletromagnéticos de superfície estimulados pela interação entre elétrons na banda de condução de metal nobre e fótons em comprimentos de onda visíveis, propagam-se ao longo da interface metal-isolante e permitem a manipulação da luz além do limite de difração clássico [7]. Os modos Sommerfeld-Zenneck, análogos dos SPPs na banda visível, podem ser suportados por metal na região THz. Metamateriais e outras estruturas artificiais, como remendos periódicos, placas perfuradas e tubos de latão, foram propostos para adaptar essas ondas de superfície fracamente ligadas [8,9,10]. Infelizmente, o confinamento pobre, a alta perda intrínseca e a capacidade de ajuste passiva desse modo têm prejudicado gravemente suas aplicações práticas.

Plasmons de grafeno, com perda relativamente baixa, sintonia dinâmica e confinamento extremo a ondas THz, possuem aplicações promissoras em dispositivos sintonizáveis de alta resolução, ultracompactos e dinâmicos. Duan et al. propor uma heteroestrutura de grafeno sintonizável por gate de banda larga para gerar e controlar de forma coerente plasmons terahertz com sintonia dinâmica e maior eficiência. Um sinal de frequência de diferença robusto pode ser gerado devido ao estreito confinamento do campo de grafeno plasmon [11]. Duan et al. em primeiro lugar, investigar o efeito discreto de Talbot em matrizes de guia de onda dielétrico grafeno plasmônico em comprimentos de onda THz, o que fornece uma nova plataforma para auto-imagem de alta resolução de ondas THz em nanoescala [12]. Lin et al. propõem um guia de onda de transparência induzida por plasmon ultracompacto, que promete aplicações potenciais em luz lenta de ondas THz [13, 14]. Li et al. propor uma série de filtros ópticos funcionais e absorvedores baseados em plasmons de material 2D, que demonstram alta integração [15], baixa perda e sintonia dinâmica [16,17,18]. A partir desses trabalhos, podemos convencer que é o confinamento extremo dos plasmons de superfície que torna possível manipular as ondas THz em profundas escalas de comprimento de onda.

Recentemente, os semimetais Dirac em massa (BDS), "grafeno 3-D", estão em foco devido à sua mobilidade de portador ultra-alta de até 9 × 10 ⁶ cm ² V ⁻¹ s ⁻¹ , que é muito maior do que o melhor grafeno de 2 × 10 ⁵ cm ² V ⁻¹ s ⁻¹ [19]. Em geral, quanto maior for a mobilidade do transportador, menor seria a perda intrínseca de plasmões. Além disso, as funções dielétricas do BDS podem ser ativamente ajustadas alterando sua energia de Fermi. A boa notícia é que BDS, como Na ₃ Bi [19], Cd ₃ Como ₂ [20], e os quasicristais AlCuFe [21], são mais fáceis de processar e mais estáveis em comparação com o grafeno, que se espera seja uma nova geração de material plasmônico após o grafeno. No entanto, o modo de confinamento de SPPs na interface BDS-isolador não é otimista. Nosso trabalho recente investigou a manipulação dos THz SPPs no guia de onda de folha BDS de camada dupla, o que indica que o modo de acoplamento simétrico tem melhor confinamento do que o modo de guia de onda plasmônica em filme BDS monocamada [22]. O índice de modo do modo simétrico é 1,21 a 1,0 THz com a energia de Fermi de BDS E _F =70 meV, o que ainda é inadequado para atender a demanda de manipulação de onda THz em escala de comprimento de onda profundo.

Neste artigo, propomos um guia de onda de metal isolante de BDS (BIM) com comprimento de sub-onda profundo com confinamento aprimorado, perda relativamente baixa e sintonia desejável. A relação de dispersão, a perda de propagação e a aplicação de filtragem deste modo altamente confinado são investigadas. Curiosamente, há uma faixa de frequência otimizada com um confinamento aprimorado, bem como uma perda reduzida, o que raramente foi relatado no modo SPP tradicional em estrutura de metal. Um confinamento de modo de banda larga até λ ₀ / 15 com uma perda relativamente baixa de 1,0 dB / λ ₀ pode ser conseguida. Diferente da estrutura baseada em BDS previamente estudada, o modo deste guia de onda BIM pode ser transmitido de forma eficiente através de uma fenda ultra estreita com largura menor que λ ₀ / 2000. Ao tomar duas fitas de silício como espelhos de reflexão, um ressonador óptico sintonizável dinamicamente foi alcançado. A frequência ressonante do ressonador pode ser sintonizada dinamicamente variando a energia Fermi do BDS, que pode encontrar aplicações na comutação e filtragem THz.

Teoria e Simulação

O guia de onda plasmônico BIM proposto é esquematicamente apresentado na Fig. 1 (a), onde o filme BDS monocamada com espessura de 0,2 μm é colocado em uma largura de lacuna g longe do substrato de prata separado pelo espaçador dielétrico com permissividade ε _r . O substrato de prata na região THz pode ser tratado como um limite perfeito do condutor elétrico (PEC). Para a luz incidente polarizada TM, o modo de guia de onda plasmônica confinado na interface metal-isolador pode se propagar ao longo do x direção com um vetor de onda k _SPP e decai exponencialmente ao longo do y direção para o espaço livre. Ao combinar as condições de contorno adequadas, o vetor de onda k _SPP do guia de ondas BIM pode ser obtido a partir da seguinte relação de dispersão:[23].
$$ - \ frac {\ varepsilon_r \ sqrt {k _ {\ mathrm {SPP}} ^ 2- {k} _0 ^ 2}} {\ varejpsilon_0 \ sqrt {k _ {\ mathrm {SPP}} ^ 2- \ frac { \ varejpsilon_r {k} _0 ^ 2} {\ varepsilon_0}}} =\ left (1+ \ frac {i \ sigma \ sqrt {k _ {\ mathrm {SPP}} ^ 2- {k} _0 ^ 2}} { {\ omega \ varepsilon} _0} \ right) \ tanh \ left (g \ sqrt {k _ {\ mathrm {SPP}} ^ 2- \ frac {\ varejpsilon_r {k} _0 ^ 2} {\psilon_0}} \ right ), $$ (1)
onde k ₀ é o vetor de ondas da luz incidente. Resolvendo a Eq. (1), podemos obter o índice de refração efetivo n _eff = k _SPP / k ₀ =Re ( n _eff ) + i Im ( n _eff ) do guia de ondas plasmônico proposto. Para os modos de guia de onda plasmônica altamente confinados, a parte real do índice de refração eficaz Re ( n _eff ) descreve aproximadamente o modo de confinamento, enquanto a parte imaginária Im ( n _eff ) é diretamente proporcional à perda de propagação do modo:Quanto maior Re ( n _eff ) é, quanto maior o confinamento. Quando g é grande o suficiente para que tanh [ g ( k _SPP ² - ε _r k ₀ ² / ε ₀ )] ~ 1, Eq. (1) seria reduzido para a relação de dispersão
$$ - \ frac {\ varepsilon_r \ sqrt {k _ {\ mathrm {SPP}} ^ 2- {k} _0 ^ 2}} {\ varejpsilon_0 \ sqrt {k _ {\ mathrm {SPP}} ^ 2- \ frac { \ varejpsilon_r {k} _0 ^ 2} {\ varepsilon_0}}} =\ left (1+ \ frac {i \ sigma \ sqrt {k _ {\ mathrm {SPP}} ^ 2- {k} _0 ^ 2}} { {\ omega \ varepsilon} _0} \ right), $$ (2)
que representa o modo de guia de onda plasmônica suportado por uma única camada de BDS sozinho. A condutividade complexa do BDS é apresentada nos métodos Eqs (3) - (4).

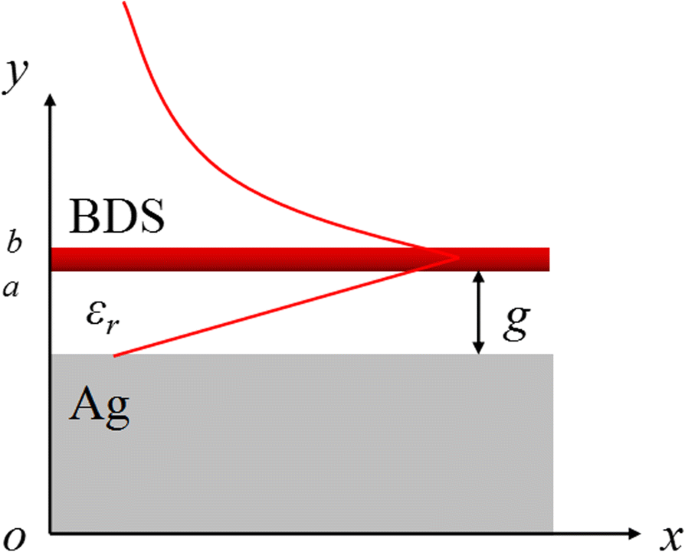
Ilustração esquemática do guia de onda plasmônica BIM:um filme BDS monocamada é colocado em uma largura de lacuna g longe do substrato de prata separado por um espaçador dielétrico com permissividade ε _r . O modo de guia de onda plasmônica TM polarizado se propaga ao longo do x direção e decai ao longo do y direção. Representação esquemática do E _x distribuição é representada pela linha vermelha

Resultados e discussão

Primeiro, demonstramos a dependência do modo de confinamento e perda de propagação do guia de onda BIM na largura da lacuna de metal BDS g e energia de Fermi E _F . Tomando E _F =70 meV, calculamos os índices de refração efetivos do modo de guia de onda SPP n _eff para diferentes valores de g , onde suas partes reais e imaginárias, Re ( n _eff ) e Im ( n _eff ), são plotados na Fig. 2a, b, respectivamente. Conforme representado na Fig. 2a, as curvas para g =10 e 100 μm se fundem em frequências superiores a 0,05 THz, o que sugere que os modos de guia de onda plasmônica estão tão confinados na interface BDS-isolador que a maioria dos campos SPP são distribuídos dentro da escala de 10 μm e a prata não funcionaria com uma largura de lacuna tão grande. Embora o modo de confinamento seja dramaticamente aprimorado após a largura da lacuna g é gradualmente reduzido de 1 μm, o menor g pesquisas, e o confinamento mais forte pode ser obtido. A tendência semelhante pode ser observada na dependência da perda de propagação na largura da lacuna g , conforme representado na Fig. 2b. Por outro lado, para uma largura de lacuna fixa menor que 1 μm, Re ( n _eff ) cada um mostra inicialmente uma redução pronunciada a um mínimo e, em seguida, exibe um comportamento gradualmente crescente, enquanto Im ( n _eff ) cada um diminui monotonicamente à medida que a frequência aumenta. Assim, há uma região de frequência otimizada onde o confinamento do modo é fortemente aumentado enquanto a perda de propagação é gradualmente reduzida. Esta característica raramente foi observada nos modos tradicionais de guia de onda plasmônica na interface metal-isolador. A Figura 2c, d mostra a dependência do modo de confinamento e perda de propagação na energia de Fermi E _F do filme BDS, onde a largura da lacuna g =1 μm. Semelhante ao caso de um guia de onda de camada dupla e monocamada, o confinamento do modo e a perda de propagação diminuem continuamente com o aumento da energia de Fermi, o que pode ser atribuído à metalicidade aumentada e ao tempo de relaxamento de portador prolongado do BDS. Por exemplo, o fator de confinamento do modo de guia de onda plasmônica em 2,5 THz pode ser de até λ ₀ / 15, onde é λ ₀ o comprimento de onda incidente, com uma perda relativamente baixa de 1,0 dB / λ ₀ quando a largura da lacuna do metal BDS é de 10 nm e a energia de Fermi é de 70 meV. Portanto, confiar em estruturas que já foram discutidas acima aumentaria o confinamento de modo com uma perda relativamente baixa, que pode ser utilizada para o projeto de filtros ópticos integrados, buffers e interferômetro de Mach-Zehnder.

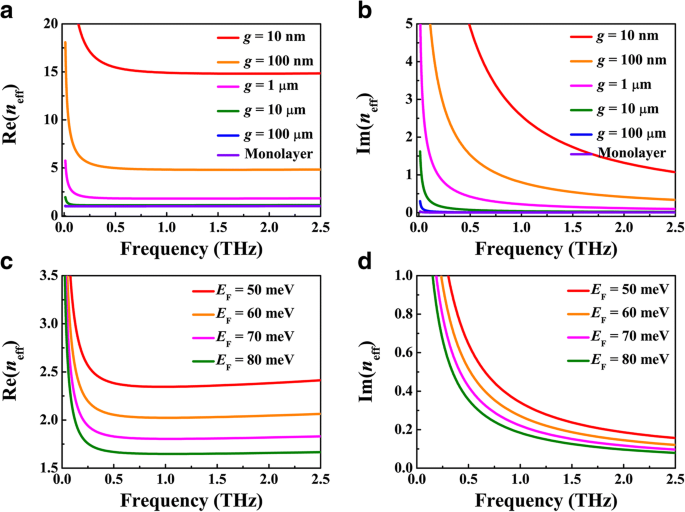
Partes reais e imaginárias do índice de refração efetivo n _eff para a , b largura de lacuna diferente g , onde a energia Fermi do BDS é fixada em E _F =70 meV e c , d diferentes valores da energia de Fermi E _F , onde a largura da lacuna é fixada em g = 1 μm

Para examinar a análise mencionada, realizamos cálculos numéricos sobre a intensidade de transmissão e distribuição de campo da estrutura de guia de ondas proposta. A configuração da simulação é descrita em métodos. Comparando com o guia de onda BDS de monocamada com a mesma energia de Fermi E _F =70 meV, a intensidade de transmissão do guia de ondas BIM na frequência de 1,56 THz é 0,97, que é maior do que a anterior, como mostrado na Fig. 3a, o que sugere que o modo de guia de ondas plasmônico na estrutura BIM sofre menor perda de propagação. Por outro lado, conforme indicado na Fig. 2a, a parte real do índice de refração efetivo de BIM em 1,56 THz Re ( n _eff ) =2,45, que é muito maior do que no caso de monocamada de 1,002. Para visualizar esta declaração, o campo magnético Hz as distribuições desses modos são apresentadas na Fig. 3b, c. Pode ser claramente verificado que o modo plasmônico altamente confinado no guia de onda BIM mostra um período de oscilação mais curto do que o do caso BDS de monocamada. Além disso, a maior parte do campo plasmônico está localizada em tal fenda estreita ~ λ ₀ / 2000, que possui aplicações promissoras em aprimoramento de campo próximo para física não linear.

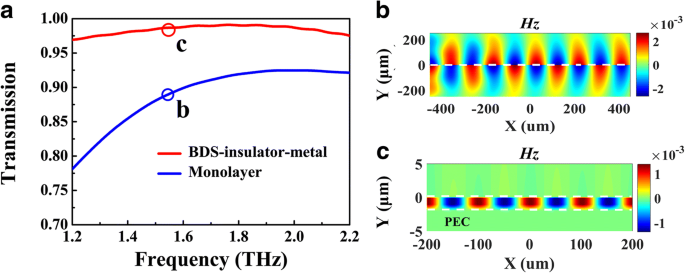
Cálculos numéricos dos espectros de transmissão ( a ) e campo magnético ( H _z ) distribuições ( b , c ) de guias de ondas BIM (curva vermelha) e monocamada (curva azul), onde E _F =70 meV, g =50 μ m, e frequência de incidente de 1,56 THz

Entre todas as aplicações mencionadas acima, o ressonador óptico é o elemento essencial para personalizar o modo de guia de onda plasmônica THz. Conforme ilustrado na Fig. 4a, dois silícios ( n _Si =3.4) [24] fitas são incorporadas ao espaçador dielétrico para formar os espelhos reflexivos, onde a onda plasmônica de propagação pode ser refletida para frente e para trás na interface silício-ar formando ressonância de onda estacionária localizada na região BIM entre as duas fitas de silício . Apenas a frequência incidente satisfaz a condição de ressonância da onda estacionária, as ondas plasmônicas podem transmitir para a saída do guia de ondas via acoplamento com o ressonador óptico projetado. A Figura 4a apresenta o espectro de transmissão do guia de onda BIM com duas fitas de silício, onde dois picos de transmissão com FWHM (largura total na metade do máximo) valores de 0,12 e 0,09 THz podem ser obviamente encontrados na frequência de 1,56 e 2,22 THz, o que demonstra uma novidade efeito de filtro passa-banda na região de terahertz. As distribuições do campo magnético (| H _z | ² ) dos picos de transmissão são representados na Fig. 4c, e, o que implica que a região BIM ensanduichada por duas fitas de silício pode ser considerada como uma cavidade de Fabry-Perot (FP). A ressonância de primeira e segunda ordem pode ser claramente encontrada na cavidade FP. A onda plasmônica incidente perto da frequência de ressonância pode ser acoplada à cavidade FP e, então, ser transmitida através do guia de ondas BIM, que gera o pico de transmissão no espectro. Enquanto, para a região de frequência não ressonante, a onda estacionária não pode ser formada e, portanto, as ondas incidentes são proibidas na porta esquerda do guia de ondas BIM, como mostrado na Fig. 4d. Além disso, combinada com a relação de dispersão do guia de ondas BIM, a intensidade de transmissão pode ser calculada analiticamente pela teoria do modo acoplado (CMT) [17]:
$$ T \ left (\ omega \ right) =\ frac {\ kappa_w ^ 2} {{\ left (\ omega - {\ omega} _0 \ right)} ^ 2 - {\ left ({\ kappa} _w + { \ kappa} _i \ right)} ^ 2}, $$ (5)
onde ω ₀ é a frequência ressonante da cavidade FP, respectivamente. Aqui, κ _w = ω ₀ / (2 Q _w ) e κ _i = ω ₀ / (2 Q _i ) são taxas de decaimento relacionadas à perda de acoplamento do guia de ondas e à perda intrínseca da cavidade FP, respectivamente. O fator de qualidade de perda total e intrínseca pode ser estimado por Q _t = ω ₀ / FWHM e Q _oi =- Re ( n _eff ) / (2Im ( n _eff )), respectivamente. Então, o fator de qualidade de perda de acoplamento do guia de ondas pode ser obtido subtraindo a perda intrínseca da perda total, a saber, Q _ei =Q _oi Q _ti / ( Q _oi - Q _ti ) [17]. Os resultados analíticos baseados no CMT apresentam boa concordância com as simulações numéricas, conforme ilustrado na Fig. 4b.

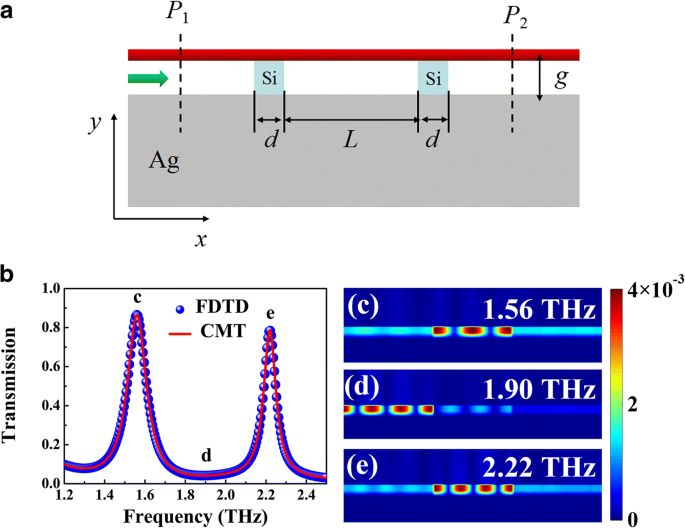
a Esquema do guia de onda BIM com fitas de silício introduzidas. A largura de cada fita de silicone é d , e a distância entre as fitas é L . b Espectros de transmissão numéricos (bolas azuis) e CMT ajustados (curva vermelha) da estrutura proposta onde g =1 μm, d =5 μm e L =120 μm. c - e Distribuições de campo magnético (| H _z | ² ) de nas frequências de incidentes de 1,56 ( c ), 1,90 ( d ), e 2.22 THz ( e )

A Figura 5 mostra a dependência da frequência de ressonância no comprimento da cavidade L , onde g =1 μm, d =5 μm e E _F =70 meV. O pico da transmissão tende a mudar para o vermelho com o aumento de L , conforme apresentado na Fig. 5a, que pode ser descrito posteriormente pela condição de ressonância de onda estacionária 2 k _SPP ( ω _r ) L + θ =2 mπ ( m =1, 2, 3, ...), onde θ é a mudança de fase reflexiva da interface silício-ar e k _SPP ( ω _r ) é o vetor de ondas do guia de ondas BIM na frequência de ressonância. Como mostrado na Fig. 5b, as frequências ressonantes do primeiro e do segundo modos realmente exibem um desvio para o vermelho com o aumento de L . De acordo com a Eq. (1), o modo de confinamento é afetado pela largura da lacuna g que, portanto, têm impacto na frequência de ressonância. A Figura 6a apresenta os espectros de transmissão para diferentes g , onde L =120 μm e E _F =70 meV. Com o aumento de g , o pico ressonante na mesma ordem exibe um deslocamento para o azul. Este fenômeno pode ser atribuído à diminuição dramática de Re ( n _eff ) como mostrado na Fig. 6c. A sintonia da energia de Fermi do BDS pode ser realizada por dopagem de superfície alcalina em experimento. A Figura 6b apresenta os espectros de transmissão para diferentes energias de Fermi, onde os outros parâmetros são os mesmos da Figura 4b. Conforme a energia de Fermi aumenta, o pico de transmissão apresenta uma mudança para o azul, que também pode estar envolvida na imagem de ressonância da onda estacionária. Para um comprimento fixo L , a cavidade FP suporta a ressonância com comprimento de onda SPP definido λ _SPP = λ ₀ / Re ( n _eff ), onde λ ₀ é o comprimento de onda do incidente. Conforme mostrado na Fig. 6c, Re ( n _eff ) é reduzido com o aumento da energia de Fermi. Como resultado, o comprimento de onda do incidente λ ₀ deve ser diminuído também para manter λ _SPP como uma constante. Essa é a razão pela qual o pico de transmissão tende a mudar para o azul com o aumento da energia de Fermi. Enquanto isso, a largura de banda do pico de transmissão é reduzida, o que pode ser atribuído à diminuição de Im ( n _eff ), isto é, a perda de propagação do modo de guia de onda plasmônica em guia de onda BIM.

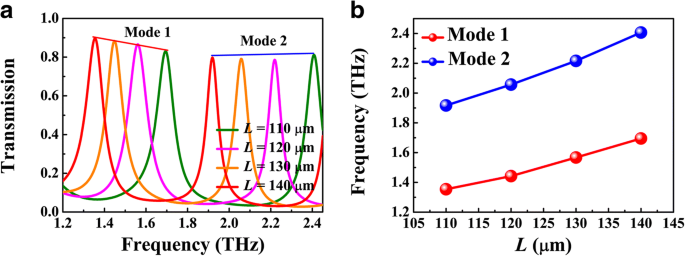
a Espectros de transmissão numérica para diferentes comprimentos de cavidades L . b Frequências ressonantes dos modos 1 e 2 em função do comprimento da cavidade L . Aqui, g =1 μm, d =5 μm e E _F =70 meV

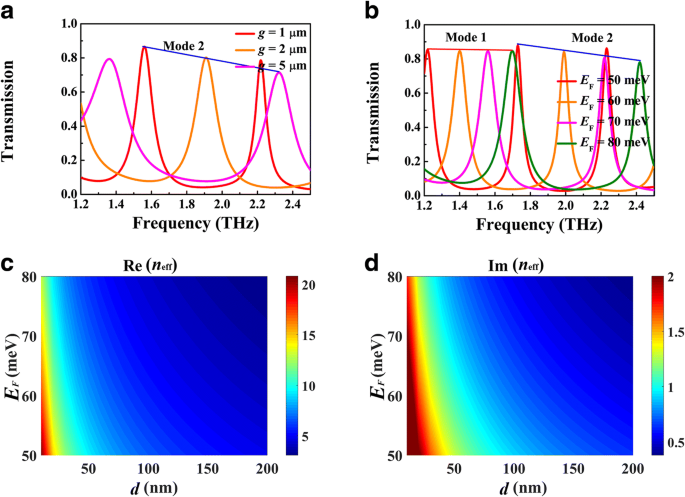
Espectros de transmissão para diferentes larguras de lacuna g ( a ) e energia de Fermi E _F ( b ), onde os outros parâmetros são iguais aos da Fig. 4b. Dependência de Re ( n _eff ) ( c ) e Im ( n _eff ) ( d ) na energia Fermi E _F e largura da lacuna g

Conclusões

Em resumo, demonstramos o modo plasmônico terahertz altamente confinado suportado por um guia de onda BIM. As características de confinamento e perda de modo foram discutidas com as variações de separação BDS-metal e energia de Fermi, o que indica que há uma faixa de frequência otimizada com confinamento de modo aprimorado, bem como perda de propagação reduzida, o que raramente foi relatado no modo SPP tradicional em estrutura metálica. Diferente da estrutura baseada em BDS previamente estudada, o modo deste guia de onda BIM pode ser apoiado de forma eficiente em uma fenda muito estreita com largura menor que λ ₀ / 2000. Ao tomar duas fitas de silício como espelhos reflexivos, um filtro passa-faixa sintonizável dinamicamente foi alcançado, onde a frequência ressonante pode ser controlada ativamente ajustando a energia Fermi do filme BDS sem reotimização de seus parâmetros estruturais.

Métodos

Os resultados numéricos são obtidos usando o método de domínio de tempo de diferença finita 2D (FDTD), onde as camadas perfeitamente combinadas são definidas para absorver a luz espalhada no x e y instruções. O tamanho da malha do filme BDS é definido como d x × d y =1 μm × 0,02 μm para alcançar uma boa convergência.

A condutividade dependente da frequência de BDS é descrita pela fórmula de Kubo com aproximação de fase aleatória [12, 25].
$$ \ operatorname {Re} \ sigma \ left (\ Omega \ right) =\ frac {e ^ 2} {\ mathrm {\ hslash}} \ frac {tk_F} {24 \ pi} \ Omega G \ left (\ Omega / 2 \ right), $$ (3) $$ \ operatorname {Im} \ sigma \ left (\ Omega \ right) =\ frac {e ^ 2} {\ mathrm {\ hslash}} \ frac {tk_F} {24 {\ pi} ^ 2} \ left \ {\ frac {4} {\ Omega} \ left [1+ \ frac {\ pi ^ 2} {3} {\ left (\ frac {T} {E_F} \ right)} ^ 2 \ right] +8 \ Omega {\ int} _0 ^ {\ varepsilon_c} \ left [\ frac {G \ left (\ varepsilon \ right) -G \ left (\ Omega / 2 \ right) } {\ Omega ^ 2-4 {\ varepsilon} ^ 2} \ right] \ varepsilon d \ varepsilon \ right \}, $$ (4)
onde G ( E ) = n (- E ) - n ( E ) e n ( E ) é a função de distribuição de Fermi-Dirac, E _F é a energia Fermi do BDS, k _F = E _F / ћv _F é o seu momento de Fermi, e v _F =10 ⁶ m / s é a velocidade de Fermi. ε = E / E _F , Ω = ћω / E _F + iћτ ⁻¹ / E _F , onde ћτ ⁻¹ = v _F / ( k _F μ ) é a taxa de espalhamento de elétrons que mostra forte dependência da mobilidade da portadora μ. ε _c = E _c / E _F ( E _c é a energia de corte além da qual o espectro de Dirac não é mais linear), e t é o fator de degenerescência quântica. Tomando AlCuFe como exemplo, os parâmetros de ajuste em nossos cálculos são definidos da seguinte forma: t =40, ε _c =3, μ = 3 × 10 ⁴ cm ² V ⁻¹ s ⁻¹ e E _F =70 meV.

Nenhum participante humano, dados ou tecido ou animais estão envolvidos nesta pesquisa.

Abreviações

BDS:: Semi-metais Dirac a granel
BIM:: BDS-isolador-metal
CMT:: Teoria do modo acoplado
FDTD:: Domínio do tempo de diferença finita
FWHM:: Largura total na metade do máximo
SPPs:: Polaritons de plasmon de superfície

Telas fibrosas à base de iodo com eletrofiação in situ para curativo antibacteriano Uma camada intermediária funcional PPy / ZnO para melhorar o desempenho eletroquímico das baterias de lítio / enxofre

Nanomateriais

Materiais Poliméricos

biológico

Corante

Especiarias