Alta absorção de fótons de fotodetectores infravermelhos de pontos quânticos obtida pelo efeito de plasma de superfície da matriz de nanofuro de metal

Resumo

Com a crescente demanda por dispositivos fotodetectores de pequena escala, os fotodetectores infravermelhos baseados em pontos quânticos têm atraído cada vez mais atenção nas últimas décadas. Neste trabalho, estruturas de matriz de nanofuros de metal periódicas são introduzidas nos fotodetectores infravermelhos de pontos quânticos para melhorar o desempenho de absortividade de fótons através do efeito de aumento de plasmon de superfície, a fim de superar o gargalo de baixa eficiência de absorção óptica que existe em fotodetectores convencionais. Os resultados demonstram que as estruturas de matriz de nanohole de metal otimizadas podem aumentar muito a absortividade de fótons em até 86,47% nos fotodetectores específicos, que é 1,89 vezes do que a de fotodetectores convencionais sem as estruturas de matriz de metal. O grande aumento da absortividade pode ser atribuído ao efeito de plasmon de superfície de acoplamento local causado pelas estruturas de matriz de nano furos de metal. Acredita-se que o estudo pode fornecer certas orientações teóricas para fotodetectores infravermelhos baseados em pontos quânticos em nanoescala de alto desempenho.

Histórico

Os fotodetectores infravermelhos semicondutores podem ser usados para detectar a luz infravermelha e têm grande aplicação promissora nos campos da pesquisa científica, imagem digital, comunicação óptica e áreas militares. Até o momento, os fotodetectores infravermelhos de pontos quânticos (QDIPs) têm atraído cada vez mais atenção nos últimos anos devido às suas excelentes propriedades de resposta à luz e tendências de miniaturização de dispositivos [1,2,3]. Embora décadas de esforços sustentados, os cientistas tenham feito grande progresso no desenvolvimento de tecnologias para a obtenção de QDIPs de alto desempenho, ainda é necessário fazer mais melhorias para atender aos desafios da miniaturização de dispositivos [4] e às demandas práticas. É apontado que a grade de metal de acoplamento na região ativa baseada em pontos quânticos pode ser considerada uma abordagem eficaz para melhorar os desempenhos dos QDIPs [5, 6], que pode render alto coeficiente de fotoabsorção pelo fotocoplamento local de aumento de plasmon efeito.

De acordo com relatos, existem dois tipos principais de estruturas de grade de metal usadas para melhorar o desempenho dos QDIPs. Uma é a estrutura de matriz de metal orifício e a outra é a estrutura de matriz de metal sem orifício. Mais concretamente, no que diz respeito à aplicação da estrutura de matriz de orifícios de metal, o grupo de Chang combinou a matriz periódica de orifícios de metal com a camada de pontos quânticos no QDIP em 2007, o que levou à transmissão de luz supernormal do fotodetector [7]. Em 2009, Lee et al. propôs um método para QDIP de alta detectividade através da integração de cristais fotônicos metálicos com um período de 3,6 µm de matriz de orifícios (espessura de 100 nm) [8]. Os resultados da pesquisa demonstram que o método pode realizar a resposta de pico do fotodetector no comprimento de onda de 11,3 μm e produzir detectividade até 30 vezes melhorada do que sem o cristal fotônico de metal. Em seguida, eles discutiram o desempenho da dependência do QDIP na luz incidente e sua aplicação na matriz de plano focal [9, 10]. Um aprimoramento de desempenho semelhante também pode ser encontrado nos relatórios usando a grade de acoplamento de matriz de metal de furo [11,12,13,14]. Estruturas de matriz de metal sem furo também são propostas. Em 2011, Huang e seus colegas de trabalho usaram a camada de nanopartículas de prata de plasmon auto-organizada para aumentar a ampla resposta espectral do QDIP e obtiveram um aumento de 2,4 ~ 3,3 vezes [15]. Em 2014, o grupo de Chen relatou que o desempenho do fotodetector pode ser aprimorado por meio do efeito de campo próximo das nanopartículas de Au [16]. Em 2015, o grupo de Ding e o grupo de Wang propuseram as estruturas de acoplamento de guia de ondas e a cavidade ressonante única do refletor de Praga distribuído [17, 18], respectivamente. Além das estruturas citadas, outras estruturas metálicas, por exemplo, o arranjo de tiras de antenas e o arranjo de nano-discos também foram discutidos e analisados [19,20,21].

No entanto, esses métodos de matriz sem orifício também podem exibir efeito aprimorado na foto-resposta dos QDIPs, mas seu processo de fabricação com métodos simples e econômicos ainda permanece um desafio em comparação com a estrutura de matriz de orifício típica. Para as estruturas de matriz de orifícios típicas, o tamanho da matriz de orifícios é comum na microescala. O aumento da foto-resposta ocorre por meio do efeito plasmon na interface entre o ar nos orifícios de metal em microescala e o semicondutor abaixo. O tamanho da matriz de orifícios de metal pode ser ainda mais diminuído para a nanoescala esperada correspondendo ao tamanho do ponto quântico no QDIP em nanoescala, quer os QDIPs de alto desempenho com efeito de aprimoramento correspondente possam ser realizados ou não. Ao mesmo tempo, mais trabalhos teóricos são necessários para elucidar os mecanismos subjacentes a esses fenômenos. Neste estudo, para tornar o fenômeno claro, os QDIPs com as estruturas de matriz de orifícios de metal em nanoescala são projetados e, mais importante em comparação com os QDIPs em microescala convencionais, o efeito de aprimoramento é explicado pela análise da condição de transmissão óptica e a distribuição do campo elétrico . Os resultados demonstram que os QDIPs com as estruturas de matriz de metal em nanoescala podem ter a absortividade de fótons de até 86,47% devido à interação fóton-ponto quântico e o acoplamento de luz eficiente, o que pode abrir a porta para o projeto e a otimização do infravermelho de nanosize fotodetector.

Modelo de design do QDIP com o Nanohole Array

Em geral, o QDIP consiste na região do ponto quântico e os eletrodos, e a região do ponto quântico é composta pela camada do ponto quântico do período e pelas camadas de barreira. Em condições ideais (ignorando as influências dos eletrodos e do substrato), a transmissão óptica de todo o QDIP pode ser considerada igual à da região do ponto quântico. Assim, os eletrodos e o substrato não são necessários para aparecer no design do QDIP. Especificamente, a Fig. 1a fornece o design do QDIP típico, que é composto de camadas compostas de pontos quânticos de 5 períodos, e essas camadas compostas são constituídas pela camada de barreira A1GaAs e as camadas GaAs, incluindo os pontos quânticos periódicos (Fig. 1b). Na configuração atual, as nanopartículas de ponto quântico são supostas como a forma de cubo que está em linha com a definição de pontos quânticos formados com muitos átomos e as moléculas e tem 40 nm de comprimento, 40 nm de largura e 7 ~ 9 nm de altura. Um modelo semelhante de pontos quânticos também pode ser encontrado na literatura relatada [22]. A área do QDIP é definida como 1000 nm × 1000 nm e a espessura das camadas de barreira AlGaAs é 60 nm. O arranjo de nanofuros de metal escolhido como Au é colocado nas camadas de nanoestrutura de pontos quânticos convencionais do QDIP convencional, que é denominado como o QDIP aprimorado exibido na Fig. 2. O raio dos furos pode ser ajustado na faixa de 50 ~ 70 nm . É notado que o material usado para formar o ponto quântico não pode ser simplesmente considerado como um material a granel com um certo índice de refração. A Figura 3 revela a característica de dispersão elétrica do material GaAs usado para formar o ponto quântico usando o método de Edward D. Palik [23]. Na figura, a curva azul e a curva vermelha representam a constante dielétrica de GaAs ε ^′ e ε ^″ , respectivamente. As Figuras 4 aeb mostram a característica de dispersão elétrica do GaAs, Al _0,3 Ga _0,7 Como material e material de ouro, respectivamente.

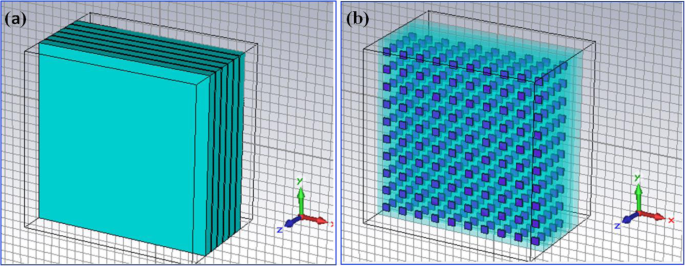
a Diagrama do modelo estrutural do fotodetector infravermelho de ponto quântico típico. b Distribuição de pontos quânticos nas regiões ativas com camadas compostas de pontos quânticos de 5 períodos. Estas camadas compostas são constituídas pela camada de barreira A1GaAs e as camadas GaAs

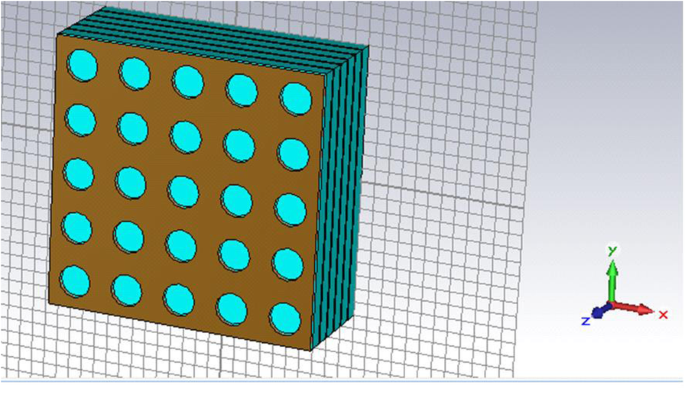
Regiões ativas de pontos quânticos com as estruturas de matriz de nano-furos de metal periódico para o QDIP aprimorado

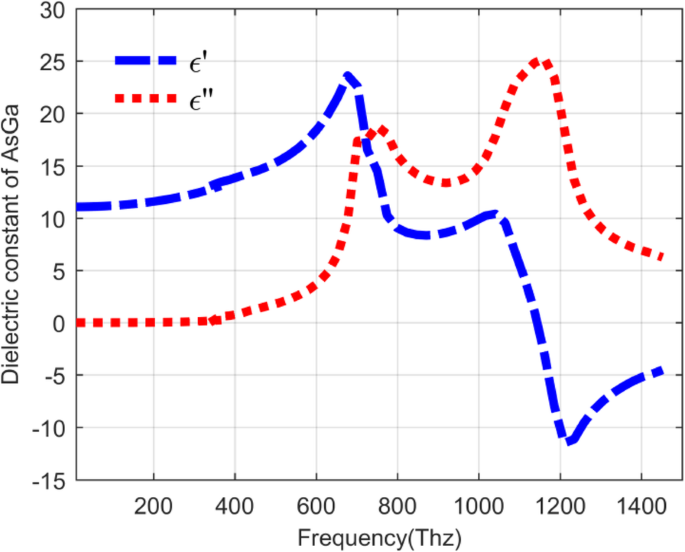
Relação de dispersão do material GaAs

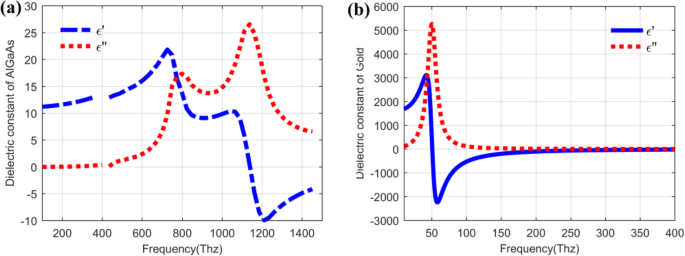
a Relação de dispersão do material AlGaAs. b Relação de dispersão do material Au

Método de cálculo baseado na célula YEE

Com base no modelo físico acima projetado, o método da integração de elementos finitos é usado para calcular a condição da transmissão óptica. Em primeiro lugar, com base nas células YEE, as equações integrais de Maxwell que satisfazem o modelo acima são escritas da seguinte forma:
$$ {\ oint} _LE \ cdot dl =- \ frac {\ partial} {\ partial t} {\ int} _SB \ cdot dS $$ (1) $$ {\ oint} _LH \ cdot dl =J + \ frac {\ partial} {\ partial t} {\ int} _SD \ cdot dS $$ (2) $$ {\ oint} _SD \ cdot dS =q $$ (3) $$ {\ oint} _SB \ cdot dS =0 $$ (4)
Em nosso cálculo, as Eqs. 1–4 são discretizados. Tanto a distribuição dos nós de campo elétrico quanto os nós de campo magnético são escolhidos no formato de “célula de Yee”. Usando a Eq. 1 como exemplo, o modelo eletromagnético do fotodetector pode ser considerado como o acúmulo de "célula de Yee". Conforme mostrado na Fig. 5, os quatro lados da célula arbitrária correspondem à Eq. 1, representando o vetor de campo elétrico e _i , e _j , e _k , e e _l . O vetor localizado na direção normal é o vetor do campo magnético b _n e, portanto, a Eq. anterior. 1 pode ser reescrito como a seguinte Eq. 5
$$ {e} _i + {e} _j- {e} _k- {e} _l =- \ frac {db_n} {dt} $$ (5)

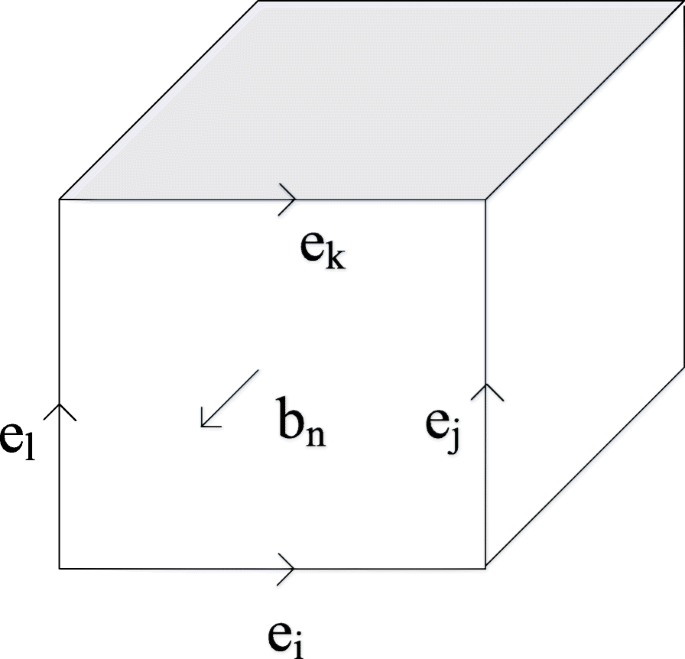
Diagrama esquemático da “célula YEE”

Adotando um método semelhante, a equação do modelo eletromagnético de todo o fotodetector pode ser escrita como:
$$ \ left [\ begin {array} {l} .. \ dots \ dots \ dots \ dots \ dots \ dots \ dots \\ {} 1 \ kern0.5em 1 \ kern0.5em -1 \ kern0.5em - 1 \\ {}. \ Dots \ dots \ dots \ dots \ dots \ dots \ dots \\ {}. \ Dots \ dots \ dots \ dots \ dots \ dots \ dots \ end {array} \ left [ \ begin {array} {l} {e} _i \\ {} {e} _j \\ {} {e} _k \\ {} {e} _l \ end {array} \ right] =- \ frac {d } {dt} \ left [\ begin {array} {l}. \\ {} {b} _n \\ {}. \\ {}. \ end {array} \ right] $$ (6)
A Equação 2 também pode ser reescrita como:
$$ Ce =- \ overset {.} {B} $$ (7)
De acordo com o método semelhante, as outras Eqs. 2 ~ 4 podem ser discretizados como:
$$ \ overset {\ sim} {C} h =\ overset {.} {d} + j $$ (8) $$ sb =0 $$ (9) $$ \ overset {\ sim} {S} d =q $$ (10)
Combinando as Eqs discretizadas. 7–10 com a condição de limite, o campo elétrico e o campo magnético podem ser resolvidos pelo método iterativo. Neste estudo, a estrutura de matriz de orifícios de metal é colocada no topo do QDIP convencional e, como tal, a estrutura pode facilitar o acoplamento de luz através do espalhamento de Bragg. A comunicação óptica correspondente é calculada posteriormente, o que pode ser discutido na seção seguinte quando a condição da transmissão, a reflexão e a absorção são fornecidas. Além disso, com base na relação entre a absorção e a eficiência quântica, a responsividade do QDIP pode ser dada. Para ser concretado, é sabido que a responsividade do QDIP como um parâmetro de desempenho muito importante pode ser calculada pela razão da fotocorrente e a potência da luz incidente [24]. Portanto, pode ser escrito como:
$$ R =\ frac {I_ {foto}} {P_o} =g \ frac {\ eta e} {hv} $$ (11)
onde eu _foto é a fotocorrente do QDIP, P é o poder da luz incidente, g é o ganho fotocondutivo, e é a carga do elétron, h é a constante de Planck, v é a frequência da luz incidente, e η é a eficiência quântica.

A eficiência quântica pode ser definida como a razão entre o número do buraco do elétron e o da foto incidente, que depende fortemente da absorção do fotodetector. Na prática, uma vez que a luz incidente ilumina diretamente a região de absorção, ela não pode ser totalmente absorvida devido ao reflexo da camada de contato superior ou da camada de metal [25, 26]. Assim, a eficiência quântica do QDIP pode ser escrita como:
$$ \ eta =\ left (1-r \ right) \ left [\ exp \ left (- {\ alpha} _0d \ right) \ right] \ left [1- \ exp \ left (- {\ alpha} _0W \ direita) \ direita] $$ (12)
onde α ₀ W é o coeficiente de absorção do QDIP, α ₀ d é o coeficiente de absorção da camada de contato incidente, r é o reflexo da camada incidente, respectivamente.

No QDIP, o ganho fotocondutivo pode ser definido como a razão do tempo de recombinação de elétrons de um estado estendido de volta para um ponto quântico τ _vida ao tempo de trânsito dos elétrons no dispositivo τ _total , e pode ser mostrado como:
$$ g =\ frac {\ tau_ {vida}} {\ tau_ {total}} $$ (13)
e sob a condição de que o tempo de trânsito em um período da camada composta de ponto quântico seja consideravelmente menor do que o tempo de recombinação de um estado estendido de volta a um ponto quântico [22, 27] _, o ganho pode ser escrito como:
$$ g =\ frac {\ left (K + 1 \ right) L \ mu E {\ left [1 + {\ left (\ mu E / {v} _s \ right)} ^ 2 \ right]} ^ { \ hbox {-} 1/2}} {\ mathrm {K} \ pi {a} _ {QD} ^ 2 {h} _ {QD} ^ 2 {\ sum} _ {QD} {V} _ {\ mathrm {t}}} $$ (14)
onde K é o número é a camada composta de pontos quânticos, L é a distância entre as camadas de pontos quânticos, μ a mobilidade dos elétrons, E é a densidade do campo elétrico no QDIP, v _s é a velocidade de saturação dos elétrons, h _QD é a altura dos pontos quânticos, ∑ _QD é a densidade de pontos quânticos em cada camada de pontos quânticos, a _QD é o tamanho lateral dos pontos quânticos e V _t é a taxa de captura de elétrons, respectivamente.

Eq. Enviada (12) e Eqs. (14) na Eq. (11), podemos obter a responsividade do QDIP, que pode ser mostrada como:
$$ R ==\ frac {\ lambda \ left (K + 1 \ right) L \ mu E {\ left [1 + {\ left (\ mu E / {v} _s \ right)} ^ 2 \ right] } ^ {\ hbox {-} 1/2} \ left (1-r \ right) \ exp \ left (- {\ alpha} _0d \ right) \ left [1- \ exp \ left (- {\ alpha} _0W \ right) \ right]} {1.24 \ mathrm {K} \ pi {a} _ {QD} ^ 2 {h} _ {QD} ^ 2 {\ sum} _ {QD} {V} _ {\ mathrm {t}}} $$ (15)

Resultados e discussão

Com base no projeto do QDIP acima, se a luz infravermelha incidente atingir o topo desses QDIPs no z - direção do eixo, os fotodetectores terão a reflexão e a transmissão da luz incidente. A absortividade dos fotodetectores pode ser determinada estudando essas condições de transmissão óptica da luz incidente, que podem desempenhar um papel muito importante na avaliação do desempenho do fotodetector. A Figura 6 apresenta suas condições de reflexão do fotodetector sem a matriz de metal (o QDIP convencional) e aquele com a matriz de metal (o QDIP melhorado). Em comparação com as duas curvas na Fig. 6, pode-se descobrir que os valores do coeficiente de reflexão do QDIP convencional são ligeiramente menores do que os do QDIP melhorado, além dos valores individuais nas faixas de frequência de 250 ~ 260 Thz e 279 ~ 293 Thz . Especificamente, tomando o valor na frequência de 219 Thz como exemplo, o valor do coeficiente de reflexão do QDIP convencional é -3,91 dB, enquanto o QDIP melhorado é tão baixo quanto -1,31 dB. Como foi dito acima, o QDIP melhorado pode ter um valor ligeiramente maior do que o QDIP convencional, mas pode-se verificar que a absorção mínima do QDIP melhorado é bastante menor do que o QDIP convencional. Para ser específico, a absorção mínima do QDIP melhorado é - 16,17 dB na frequência de 255,10 Thz, enquanto o valor para o QDIP convencional é igual a - 13,42 dB a 254,86 Thz. O baixo coeficiente de reflexão do QDIP melhorado pode ser atribuído ao maior coeficiente de absorção do metal do que no semicondutor para luz infravermelha. A absorção pode ser calculada com base nas contribuições comuns da reflexão e da transmissão. A Figura 7a representa o coeficiente de transmissão do QDIP convencional e seus valores marcados com a cor azul são claramente maiores do que aqueles do QDIP aprimorado dentro da faixa de frequência total de 200 ~ 340 Thz. Por exemplo, na frequência de 298 Thz, o coeficiente de transmissão do QDIP melhorado é apenas - 10,83 dB, que é 1,60 vezes menor do que o do QDIP convencional, que é - 4,15 dB. De acordo com a relação competitiva entre a transmissão, o reflexo e a absorção, a diminuição do coeficiente de transmissão levará ao aumento da absorção sob a condição de ignorar outras perdas da luz incidente.

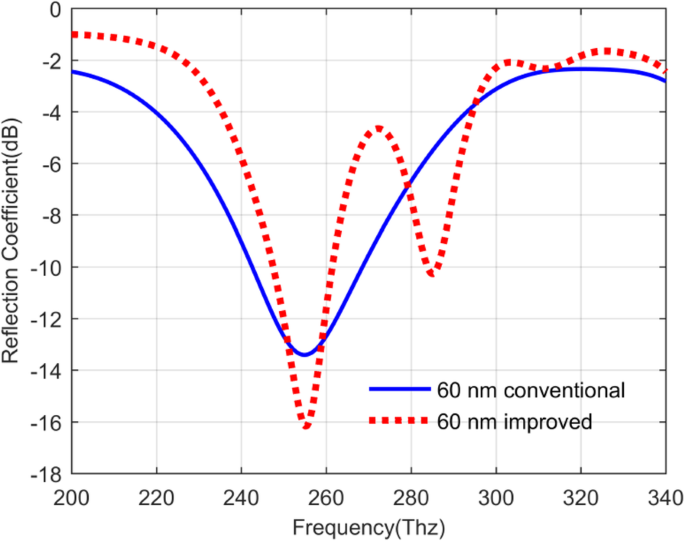
Coeficientes de reflexão do QDIP convencional sem matriz de metal (curva azul) e do QDIP aprimorado com matriz de nanofuro de metal (curva vermelha)

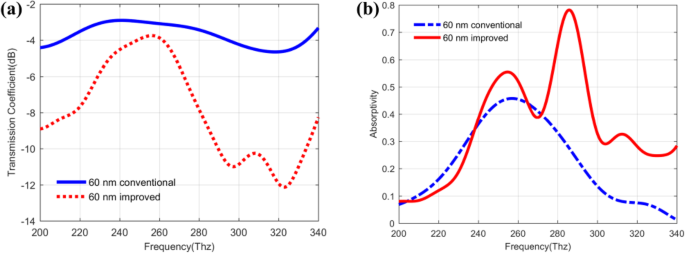
Coeficientes de transmissão ( a ) e coeficientes de absortividade ( b ) do QDIP convencional e do QDIP melhorado, respectivamente

Combinada a situação de transmissão na Fig. 7a com a situação de reflexão na Fig. 6, a absortividade do QDIP pode ser calculada, que é mostrada na Fig. 7b. Na figura, a curva vermelha (marcada como 60 nm melhorado) descreve a absortividade do QDIP melhorado com a estrutura de metal, e a outra curva azul representa o QDIP convencional sem a estrutura de furo de metal (marcado como 60 nm convencional). Fazendo uma comparação entre as duas curvas, pode-se verificar que a absortividade do QDIP melhorado é maior do que a do QDIP convencional. O máximo da absortividade do QDIP melhorado é 0,782 na frequência de 286 Thz, que é 1,71 vezes maior do que o do QDIP convencional, que é apenas 0,458 na frequência de 257 Thz. As razões para o aumento da absortividade do QDIP melhorado podem ser explicadas a seguir. As estruturas de matriz de nanofuros de metal são introduzidas no topo do QDIP convencional e tal configuração pode favorecer o efeito de ressonância de plasmon de superfície, levando ao efeito de acoplamento local da luz incidente. Além disso, o efeito de acoplamento local pode fazer com que mais luz incidente entre nas camadas de pontos quânticos semicondutores abaixo, o que pode resultar em alta absorção para a luz incidente e ter melhores propriedades fotoelétricas com maior fotocorrente e maior eficiência quântica.

Para deixar claro como realizar o efeito de aumento do plasmon nos QDIPs aprimorados, também estudamos as influências das diferentes estruturas de nano furos de metal na absortividade dos QDIPs aprimorados. Como mostrado na Fig. 8a, as curvas de absortividade dos QDIPs melhorados com diferentes raios de nanohole de metal correspondem à curva preta (50 nm), verde (55 nm), vermelha (60 nm) e azul (65 nm), respectivamente. Os valores de absortividade do QDIP melhorado revelam as diferentes tendências de mudança em diferentes nanofuros. Os valores de pico da absortividade para o QDIP melhorado é 0,744 (curva preta em 289 Thz), 0,721 (curva verde em 291 Thz), 0,782 (curva vermelha em 286 Thz) e 0,707 (curva azul em 288 Thz), respectivamente. Obviamente, entre esses fotodetectores, o QDIP aprimorado com um raio de furo de 60 nm pode ter o melhor desempenho de absortividade. Ao mesmo tempo, é sabido que a espessura da camada metálica do orifício também pode ter influências na absortividade. Conforme demonstrado na Fig. 8b, quando a espessura da camada de metal no QDIP melhorado é alterada de 10 para 40 nm, os valores de pico da absortividade mudam correspondentemente de 0,667 (263 Thz para a espessura de 10 nm) para 0,782 (286 Thz para 20 nm), 0,662 (293 Thz para 30 nm) e 0,590 (262 Thz para 40 nm). Dentre esses valores de pico, a camada de nanofuro de metal com espessura de 20 nm pode ter o maior valor de absortividade.

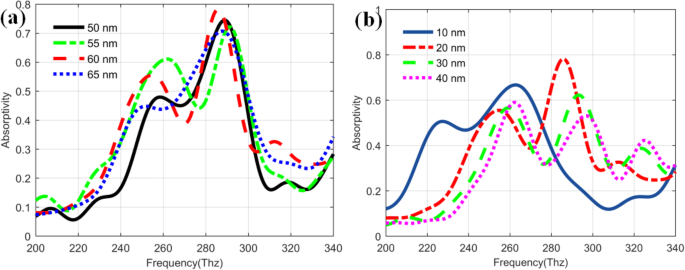
Absorvência do QDIP melhorado ( a ) com diferentes raios e diferentes espessuras de metal de nanofuros de metal ( b)

Para tornar o fenômeno acima claro, estudamos mais as condições de distribuição do campo elétrico na superfície superior do QDIP aprimorado com os diferentes raios dos orifícios de metal em 286 Thz. A Figura 9 revela a distribuição do campo elétrico em diferentes raios de orifícios de metal na faixa de 50–65 nm. Comparado as quatro imagens na Fig. 9a, é claro que os QDIPs com o raio do orifício de 50 nm (Fig. 9a) e 55 nm (Fig. 9b) podem ter um aumento de campo elétrico relativamente mais fraco devido às distribuições de campo elétrico correspondentes em As Fig. 9 aeb encontram-se em toda a área incluindo os furos e suas regiões adjacentes e, portanto, seus efeitos de acoplamento local do campo elétrico podem ser ignorados, enquanto a área de acoplamento local do campo elétrico com um campo elétrico elevado pode ser observada na Fig. 9 c e d. As fortes distribuições de campo elétrico em torno dos orifícios na Fig. 9c ed com a forma do anel podem estar localizadas na interface entre os orifícios de metal e o ar nos orifícios de metal como resultado do efeito de acoplamento de plasmon de superfície. Comparado com as distribuições do campo elétrico na Fig. 9c ed, o efeito de acoplamento do campo elétrico na Fig. 9c é mais forte do que na Fig. 9d de acordo com suas cores marcadas que são uma mistura de vermelho, verde e azul. Nesse sentido, a cor vermelha representa o campo mais forte, e a cor azul representa o campo mais fraco. Com base na análise acima, os nanofuros de metal com raio de 60 nm geram o efeito de campo elétrico de realce pelo plasmon de superfície. Para tornar ainda mais claro o efeito de realce, a distribuição do campo elétrico em xz - plano correspondente à absorção máxima do QDIP otimizado na frequência de 286 Thz em nosso estudo, conforme mostrado na Fig. 10a, que se encontra na seção y =0 (correspondendo ao campo do xz -avião). Na figura, da direção de z No eixo, a distribuição do campo elétrico aprimorado fica na região entre os orifícios de metal adjacentes, marcada com a cor vermelha, e o campo fraco, na região dos orifícios de metal marcados com a cor azul. A distribuição do campo elétrico revela diretamente a absorção aprimorada do QDIP. É o efeito de acoplamento de aprimoramento que leva ao aumento da absortividade e, além disso, leva à alta eficiência quântica do QDIP aprimorado. Claro, as mesmas conclusões também podem ser tiradas analisando a distribuição do campo magnético de acordo com as propriedades das propriedades eletromagnéticas da luz. Devido à discussão da distribuição do campo magnético ser a mesma que da distribuição do campo elétrico, não há necessidade de discuti-la neste estudo.

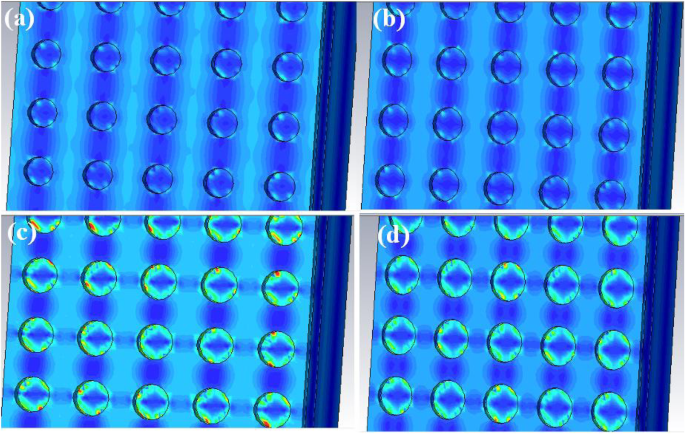
Distribuição do campo elétrico dos QDIPs melhorados com diferentes raios de nanofuros de metal: a r =50 nm, b r =55 nm, c r =60 nm e d r =65 nm

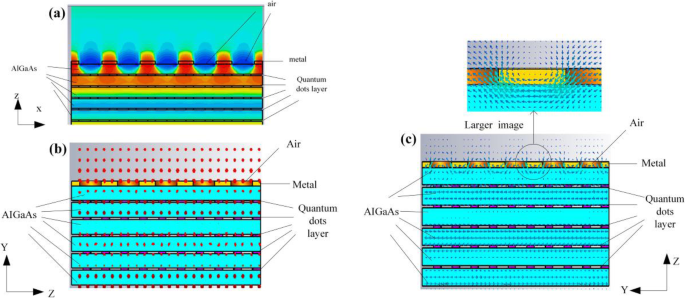
a x campo eletrônico de direção do QDIP otimizado. b Polarização do campo elétrico do QDIP melhorado. c Polarização de campo magnético do QDIP melhorado

Além disso, como foi dito acima, o efeito de intensificação é do plasmon de superfície e o modo da onda de plasmon de superfície excitada é posteriormente determinado. As Figuras 10a eb exibem os resultados do campo elétrico e magnético. Na figura, a Fig. 10b exibe a distribuição de polarização do campo elétrico em yz -avião. Pode-se ver que o campo elétrico é normal ao yz -avião, ou seja, o campo elétrico não pode ter o E _z componente. A Figura 10c apresenta a distribuição de polarização do campo magnético. Pode-se verificar que o campo magnético é paralelo ao yz -plano, isto é, há o componente Hz na direção de propagação da luz incidente que é z -direção. Portanto, em nosso estudo, a onda de plasma de superfície excitada é o modo TE. Além disso, para deixar clara a posição usada para excitar o plasmon de superfície, a distribuição do campo magnético perto da interface do furo de metal é mostrada no topo da Fig. 10c. Pode-se ver que o campo magnético na posição entre os furos de metal adjacentes é mais forte do que nos furos de metal. Além disso, de acordo com o campo elétrico apresentado na Fig. 10a, também pode provar que o campo de realce está concentrado no local entre os orifícios metálicos adjacentes. Portanto, pode-se concluir que o efeito do plasmon de superfície pode ser da superfície entre o metal e o semicondutor, que fica na posição entre os orifícios metálicos adjacentes. Claro, é importante notar que o aumento da absorção não é apenas do plasmon de superfície, mas também da reflexão aumentada da camada de metal, levando à absorção secundária da luz incidente, uma vez que a luz incidente é iluminada no QDIP ao longo eixo z.

É bem sabido que os parâmetros relacionados às camadas metálicas também podem ter grande influência no desempenho do QDIP. A fim de determinar os parâmetros ideais, a espessura da camada de barreira e a camada de pontos quânticos são posteriormente analisadas e discutidas sob as condições de espessura da camada de metal otimizada (20 nm) e raio do furo de metal (60 nm). A Figura 11a mostra a tendência de mudança da absortividade dos fotodetectores com as diferentes espessuras da camada de barreira na faixa de 70-85 nm. A partir da imagem, essas curvas de absortividade têm a tendência de mudança semelhante. Quando as espessuras da camada de barreira variam na faixa de 70 ~ 85 nm, os valores de absortividade máximos correspondentes dos QDIPs melhorados são 0,7581 (70 nm, em 322,78 Thz), 0,7763 (75 nm, em 304,84 Thz), 0,8552 (80 nm, a 292,75 Thz) e 0,8346 (85 nm, a 284,17), respectivamente. Comparado com esses valores máximos de absortividade, pode-se descobrir que a camada de barreira com a espessura de 80 nm pode ter o melhor desempenho de absortividade para os QDIPs aprimorados. Outros parâmetros fixos com os valores otimizados acima, as influências das espessuras da camada de pontos quânticos no desempenho de absortividade para o QDIP melhorado são estudadas posteriormente e as curvas correspondentes são mostradas na Fig. 11b. A partir da figura, pode-se descobrir que a curva vermelha pode ter o valor máximo de absortividade de 0,8647 na frequência de 295,48 Thz para o QDIP melhorado com a espessura da camada de 7 nm, o que ilustra que o fotodetector pode ter o estado de transição ideal.

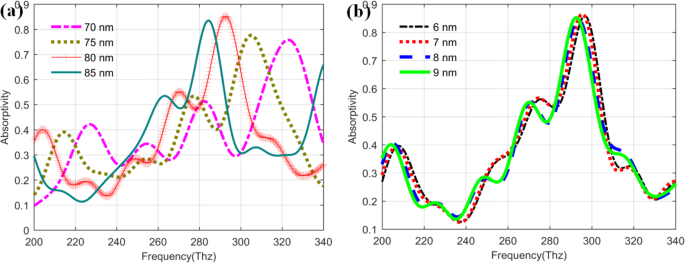
Absorvência do QDIP melhorado com as diferentes espessuras de a a camada de pontos quânticos e b camada de barreira

Com base na discussão acima, é claro que não apenas os parâmetros relacionados ao QDIP podem ter influências no desempenho do dispositivo, mas também a espessura da camada de pontos quânticos e a camada de barreira também podem determinar o desempenho do dispositivo. Neste estudo, de acordo com os resultados do cálculo teórico, os parâmetros otimizados para os QDIPs melhorados podem ser dados com a espessura da camada de metal de 20 nm, o raio do furo do metal de 60 nm, a espessura da camada de pontos quânticos de 7 nm e a camada de barreira espessura de 80 nm. A absortividade do fotodetector ideal pode ser tão alta quanto 0,8647. Além disso, comparando o QDIP convencional com o QDIP otimizado, conforme mostrado na Fig. 12, os valores de absortividade na curva vermelha são bastante maiores do que na curva azul, além dos valores na faixa de frequência de 222,91 ~ 262,18 Thz. A absortividade máxima na curva vermelha é igual a 0,8647 na frequência de 295,48 Thz, que é 1,89 vezes maior do que na curva azul (que é a mesma que a curva anterior marcada "60 nm convencional" na Fig. 7b correspondendo a o QDIP sem matriz de orifícios de metal) na frequência de 257 Thz. A mudança de frequência para o pico de absortividade máxima resulta principalmente da mudança na espessura do fotodetector melhorado. Além disso, com base nos parâmetros otimizados dos QDIPs, as espessuras da camada de pontos quânticos e da camada de barreira, o valor de eficiência quântica e a responsividade do fotodetector são calculados.

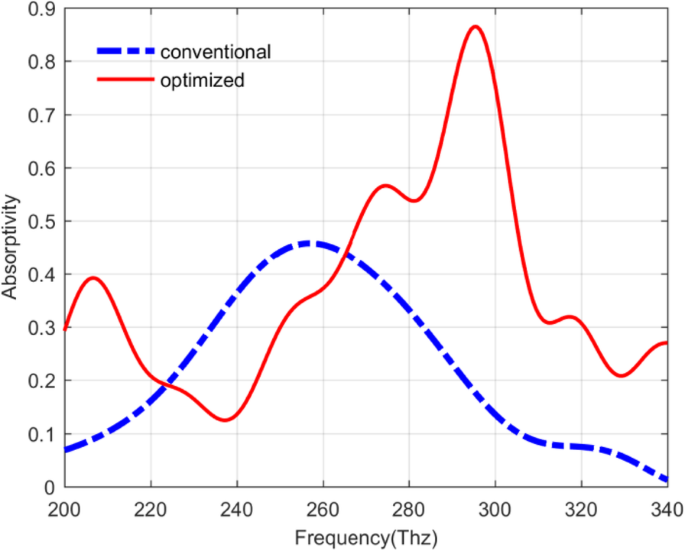
Absorptivity of the conventional QDIP in blue curve and improved QDIP in red curve with the barrier layer thickness of 80 nm

Quantum Efficiency and Responsivity of the QDIP

Based on the calculated results of the absorptivity in Fig. 12 as well as combining with the expression of the quantum efficiency and the responsivity of the QDIP above, the quantum efficiency of the QDIP and the responsivity can be calculated out, and the corresponding results are plotted in Fig. 13 a and b. Figure 13a depicts the quantum efficiency of the QDIP. In this figure, the blue dotted curve represents the quantum efficiency of the QDIP without metal array, the other red full curve is that of the optimized QDIP with metal array. Making a comparison between the two curves, it can be observed that the maximum quantum efficiency of the optimized QDIP is 0.2961 at the frequency of 295.87 Thz, and it is 1.205 times than that of the conventional QDIP, which is equal to 0.2458 at the frequency of 256.48 Thz. The increasing trend is similar to the absorptivity provided in Fig. 12 which results from the introduction of the metal hole array and the optimization of the quantum dot infrared photodetector. Based on the increasing trends for the absorptivity, we can find that the responsivity of the QDIP also reveals similar increasing trends. To be specific, Fig. 13b gives the responsivity of the optimized QDIP and the conventional QDIP, respectively. In the figure, the red curve is on behalf of the responsivity of the conventional QDIP, and the blue curve stands for that of the optimized QDIP with the metal holes layer. Similar to the analysis in Fig. 13a, the responsivity is 0.0326 mA/W at the frequency of 295.87 Thz, which is 0.0174 larger than that of the conventional QDIP at the frequency of 256.48 Thz (which is 0.0152). The increase in the responsivity can be proven in the other frequency band in the range of 229.57~254.41 Thz, which obviously demonstrates the enhancement in the performance of the photodetector due to the introduction of the metal hole array and the optimization of the quantum dot regions. Moreover, the reasons for the enhancement were detailedly discussed in detail analyzing the electric field distribution of quantum dot regions above.

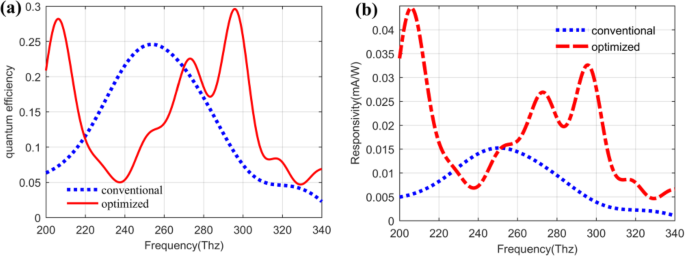
a Quantum efficiency of QDIP. b Responsivity of QDIP

Influence of the Electrodes and the Substrate

What was studied above is all under the condition of ignoring the influence of the electrodes and the substrate; in fact, the electrodes and the substrate can have certain influences on the performance, but they do not influence the description of the enhancement effects of the performance of the optimized QDIP with the metal layer. This is because the electrodes and the substrate can have almost the same influence on the absorption of the QDIP with the metal layer and without the metal layer. To illustrate the issue adequately, we recalculated the absorption of the QDIP considering the influence resulting from the substrate and the electrodes as well as the quantum efficiency, the responsivity, and so on. To be concrete, it is well known that the electrodes are generally designed at the two ends of the absorption region of the quantum dots, and thus, as shown in Fig. 14a, one is at the top of the conventional QDIP and the other is at the bottom end of the absorption region of the QDIP. That is to say, it lies at the top of the substrate, which can provide the quantum dot absorption region with the bias voltage and transmit current together with the electrodes said above. Here, it is worth mentioning that there is the metal hole array instead of the metal ring in the optimized QDIP in our study used as the electrodes. The other electrode is similar to that of conventional QDIP. Based on the above design, a concrete distribution of the electrodes is clearly calculated in Fig. 14a. Similar to Fig. 14a, in Fig. 14 b, the material of the electrodes is chosen as gold, and the substrate is chosen as AlGaAs; their thicknesses are 20 nm and 300 nm, respectively.

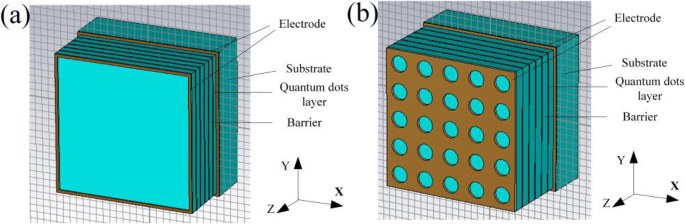
a Conventional QDIP with electrodes and substrate. b Optimized QDIP with the electrodes and substrate

Based on the introduction of electrodes and substrate in the structure of the QDIP above, we calculated the absorption of the QDIPs, and the corresponding results are compared with the QDIP without the electrodes and the substrate. Figure 15 demonstrates the influence of the electrodes and substrate on the absorptivity of the QDIP. In the figure, the blue curve and the pink curve are the absorptivity of the conventional QDIP without the electrodes and the substrate and that of the optimized QDIP without the electrodes and the substrate, respectively. The red dashed curve represents the absorptivity of the optimized QDIP with the electrodes and the substrate. Its maximum absorption is 0.7620 at the frequency of 304.35 Thz which is just 0.1027 smaller than that of the optimized QDIP without electrodes and substrate. The decrease of the absorptivity is degraded from the loss of the electrodes and the substrate, the same as the green curve with the absorptivity of the conventional QDIP with the electrodes and substrate. Compared with the absorptivity of the conventional QDIP and optimized QDIP with electrodes and substrate, the enhancement is very clear in the absorptivity of the optimized QDIP with electrodes and substrate, which is the same as the optimized QDIP in Fig. 12. In other words, though the electrodes and the substrate can result in the decrease of the absorptivity, the total absorptivity of the optimized QDIP can be enhanced compared with that of bare QDIP, and thus, the decrease can be negligible as they can have a very small influence on the description of the enhancement of the optimized QDIP when using the metal hole array.

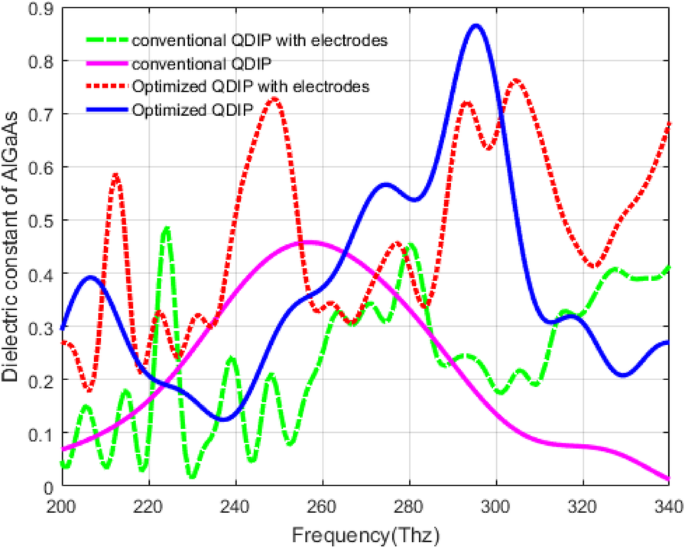
Absorption of the QDIP with electrodes and substrate

In addition, it can be observed that the change trend of the absorptivity of the QDIP with the electrodes and substrate cannot be the same as the previous curves (corresponding to the blue curve and pink curve). They are more complex with many peak values. The reasons for this phenomenon can be explained as follows. First of all, the addition of the electrodes and the substrate can produce more or less a loss and the frequency shifts due to the accumulated heating effect and the other negative influence factors. Secondly, since the material of the electrodes is chosen as the metal, in the optimized QDIP with the electrodes and the substrate, it can result in enhanced reflection and enhanced surface plasmon. The two reasons commonly favor the enhancement of the absorptivity as demonstrated in Fig. 15.

Conclusões

In conclusion, the conventional QDIP performance can be greatly improved by adding the nanoscale metal nanohole array, and the enhanced mechanism of the performance for improved QDIPs is discussed by analyzing the reflection, the transmission, the absorption, and the distribution of the electric field. The results not only demonstrate that the improved QDIPs can have higher absorptivity than that of conventional QDIPs but also indicate that the parameters of the improved QDIPs related to the metal nanohole array together with the quantum dot composite layer can significantly influence their performance. According to theoretical calculation, the optimized parameters of the improved photodetectors are 20 nm in metal layer thickness, 60 nm in metal hole radius, 7 nm in quantum dot layer thickness, and 80 nm in barrier layer thickness. The maximum absorptivity value of the optimized photodetector can be as high as 86.47% at the frequency of ~ 300 Thz. The great enhancement of the absorptivity can be attributed to the local coupling effect caused by the enhancement of the electric field effect via the surface plasmon, and further leads to the high quantum efficiency and responsivity, which are 0.2961 and 0.0326 mA/W, respectively. It is believed that the current contribution could provide certain theoretical guidance for developing nanoscale QDIPs with high performance.

Disponibilidade de dados e materiais

Todos os dados estão totalmente disponíveis sem restrição.

Abreviações

QDIPs:: Quantum dot infrared photodetectors

Fig

Figura

Eqs

Equations

Fulerenol solúvel em água com dependência de grupo hidroxila para inativação eficiente fotodinâmica excitada por dois fótons de micróbios infecciosos Engenharia de deformação nas propriedades eletrônicas e ópticas de WSSe Bilayer

Nanomateriais

Materiais Poliméricos

biológico

Corante

Especiarias