Dinâmica de magnetização modulada por Dzyaloshinskii-Moriya Interação na junção do túnel magnético de torque de transferência giratória de interface dupla

Resumo

Atualmente junções de túnel magnético de interface dupla (MTJs) foram desenvolvidas para aumentar a barreira de estabilidade térmica no nó de tecnologia em nanoescala. A interação Dzyaloshinskii-Moriya (DMI) existe inevitavelmente em tais dispositivos devido ao uso de estruturas de metal pesado / ferromagneto. Estudos anteriores demonstraram o efeito prejudicial do DMI nos MTJs convencionais de torque de transferência de rotação (STT) de interface única. Aqui, neste trabalho, iremos provar que o efeito prejudicial do DMI poderia ser quase eliminado no STT-MTJ de interface dupla. Esta conclusão é atribuída ao efeito de supressão da interação Ruderman – Kittel – Kasuya – Yosida (RKKY) no DMI. Os mecanismos detalhados são analisados com base nos modelos teóricos e resultados de simulação micromagnética. Nosso trabalho destaca a importância de controlar adequadamente o DMI na camada livre composta da interface dupla STT-MTJ.

Introdução

A memória de acesso aleatório magnético (MRAM) é um dos candidatos mais promissores para a memória não volátil de próxima geração, graças ao seu baixo consumo de energia, alta densidade, velocidade de acesso rápido, resistência quase infinita e boa compatibilidade com a tecnologia CMOS [1, 2]. O dispositivo elementar do MRAM é a junção do túnel magnético (MTJ), que é composta por uma barreira de túnel imprensada entre duas camadas ferromagnéticas (denominadas camada fixada e camada livre). Beneficiando-se do progresso na anisotropia perpendicular, o tamanho do traço da MTJ foi escalado abaixo de 40 nm ou mesmo 1 × nm [3,4,5]. No entanto, um desafio para o MTJ sub-40 nm é manter a barreira de estabilidade térmica adequada E = μ ₀ M _s H _k V / 2. (com μ ₀ a permeabilidade magnética do vácuo, M _s a magnetização de saturação, H _k o campo de anisotropia, V o volume da camada livre). Conforme indicado por esta equação, E diminui com o dimensionamento do MTJ, resultando em uma redução do tempo de retenção de dados. Para superar esse desafio, MTJs de interface dupla foram propostos para atingir E suficientemente alto no nó de tecnologia sub-40 nm [6,7,8,9,10]. Usando duas camadas ferromagnéticas acopladas como a camada livre de compósito, o volume equivalente ( V ) no MTJ de interface dupla é aumentado para aumentar a barreira de estabilidade térmica. Enquanto isso, a constante de amortecimento é diminuída para manter uma corrente de comutação baixa.

Nos MTJs de interface dupla, a estrutura de ferromagneto / metal pesado (FM / HM) desempenha um papel importante na otimização do desempenho. Por outro lado, a estrutura FM / HM aumenta o acoplamento spin-órbita (SOC) para induzir a anisotropia perpendicular. Por outro lado, o metal pesado funciona como um espaçador entre duas camadas ferromagnéticas da camada livre composta para fornecer a interação Ruderman – Kittel – Kasuya – Yosida (RKKY) [11], que acopla ferromagneticamente as magnetizações das duas camadas ferromagnéticas em para que se comportem como uma camada idêntica. Além disso, trabalhos recentes demonstram que o forte SOC do metal pesado combinando com os spins atômicos do ferromagneto poderia formar um acoplamento de troca antissimétrico chamado interação Dzyaloshinskii-Moriya (DMI) [12, 13]. Portanto, o DMI é induzido naturalmente no MTJ de interface dupla com estruturas FM / HM. O DMI favorece as texturas magnéticas quirais (por exemplo, espirais de spin, skyrmions e paredes de domínio do tipo Neel) e afeta dramaticamente a dinâmica da magnetização, conforme validado por estudos recentes [14,15,16,17,18,19,20,21 , 22,23,24,25]. É importante mencionar que o papel do DMI se tornará mais complicado no MTJ de interface dupla, uma vez que duas interfaces FM / HM precisam ser consideradas em conjunto com uma interação RKKY adicional. Portanto, é importante revelar o efeito do DMI no MTJ de interface dupla.

Nesta carta, pela primeira vez, estudamos o processo de comutação dos MTJs de interface dupla sob as ações de interação DMI e RKKY. O MTJ de interface dupla é comutado pelo torque de transferência de rotação (STT), que é uma abordagem convencional para a gravação de dados do MRAM. Foi relatado recentemente que o DMI tem um efeito prejudicial na comutação STT [21, 22]. Aqui, nossos resultados demonstram que em MTJs de interface dupla, o efeito prejudicial do DMI pode ser suprimido pela interação RKKY, resultando em uma comutação rápida e dinâmica mais uniforme. Nosso trabalho comprova a robustez do STT-MTJ de interface dupla contra o efeito interfacial negativo.

Métodos

O dispositivo estudado neste trabalho é ilustrado na Fig. 1a, com uma estrutura FM / HM / FM como camada livre composta. A espessura da camada HM é ajustada a um valor apropriado para que a interação RKKY induzida acople ferromagneticamente duas camadas FM. Uma das camadas FM é magneticamente mais macia, que é denotada como FL1 (camada livre 1), enquanto a outra é magneticamente mais dura e denotada como FL2 (camada livre 2). Para alternar a magnetização da camada livre de compósito, uma corrente é aplicada à interface dupla MTJ e gera o STT. Neste trabalho, consideramos apenas o STT transmitido da camada de referência para FL1, enquanto os outros torques entre FL1 e FL2 são desprezados. Este modelo simplificado é consistente com os trabalhos relatados anteriormente [26,27,28]. Os DMIs são induzidos nas interfaces FM / HM e HM / FM e têm sinais opostos devido à quiralidade diferente [29].

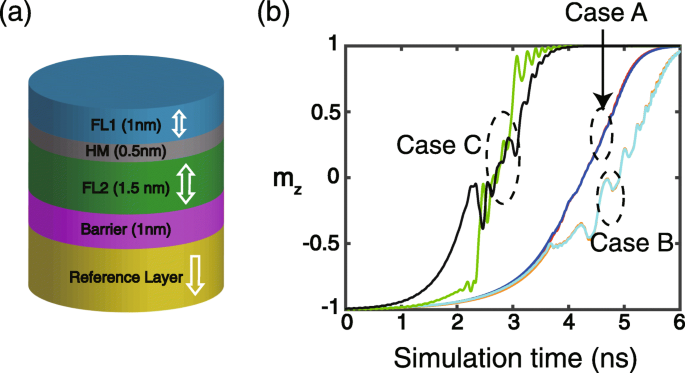
a Estrutura esquemática do dispositivo estudado neste trabalho. As outras camadas não são mostradas para maior clareza. b Resultados típicos do dependente do tempo m _z (componente perpendicular da magnetização da unidade). Caso A:σ =1 × 10 ⁻³ J / m ² , D ₁ = D ₂ =0 (vermelho para FL1, azul para FL2). Caso B:σ =1 × 10 ⁻³ J / m ² , D ₁ =1 mJ / m ² , D ₂ =-1 mJ / m ² (laranja para FL1, ciano para FL2). Caso C:σ =1 × 10 ⁻⁴ J / m ² , D ₁ = D ₂ =0 (verde para FL1, preto para FL2)

A dinâmica de magnetização do FL1 e FL2 na interface dupla MTJ é estudada por simulação micromagnética. A evolução temporal do vetor de magnetização unitária é governada pela seguinte equação de Landau-Lifshitz-Gilbert (LLG). Escolhemos o pacote OOMMF, uma ferramenta de simulação micromagnética de código aberto [30], para modelar a estrutura do dispositivo e resolver a equação LLG para analisar a dinâmica da magnetização.
$$ \ frac {\ partial \ mathbf {m}} {\ partial t} =- \ gamma \ mathbf {m} \ times {\ mathbf {H}} _ {eff} + \ alpha \ mathbf {m} \ times \ frac {\ partial \ mathbf {m}} {\ partial t} + \ gamma \ frac {\ mathrm {\ hslash}} {2e} \ frac {\ eta} {M_s {t} _F} J \ mathbf {m } \ times \ left (\ mathbf {m} \ times \ mathbf {z} \ right) $$
onde γ é a razão giromagnética, m é o vetor unitário ao longo da magnetização, z é o vetor unitário ao longo da direção da espessura, H _eff é o campo efetivo incluindo anisotropia perpendicular uniaxial, energia de troca de 6 vizinhos, campo DMI, interação RKKY, campo de desmagnetização, interação dipolar e STT. Outros parâmetros e seus valores padrão estão listados na Tabela 1, a menos que indicado de outra forma. Esses valores de parâmetro estão de acordo com as tecnologias de ponta. Quanto à magnitude do DMI, consideramos uma camada livre do compósito CoFeB / W / CoFeB na interface dupla MTJ [10, 31,32,33]. Os resultados experimentais de DMI relatados de W / CoFeB variam de 0,12 mJ / m ² a 0,73 mJ / m ² [34,35,36]. Em nossa simulação, estendemos o intervalo de magnitude DMI para ± 2 mJ / m ² para um estudo geral.

A energia RKKY entre um par de momentos magnéticos m _i e m _j é definido como E _ij = σ [1 - m _i ∙ m _j ] / ∆ _ij , onde m _i e m _j são momentos magnéticos de FL1 e FL2, respectivamente. σ é o coeficiente de troca de superfície bilinear entre duas superfícies. ∆ _ij é o tamanho da célula de critério na direção da célula i em direção à célula j . Neste trabalho FL1 e FL2 são acoplados ferromagneticamente, então σ > 0, o que significa que a interação RKKY tende a fazer m _i paralelo a m _j . O DMI atua nos spins atômicos vizinhos S ₁ e S ₂ através de um terceiro átomo com grande SOC. Hamiltoniano DMI correspondente é expresso como H _DM =- D ₁₂ ∙ ( S ₁ × S ₂ ), onde D ₁₂ é o vetor DMI [37]. Portanto, o DMI degrada a uniformidade entre S ₁ e S ₂ , que compete com a interação RKKY.

Resultados e discussão

Em primeiro lugar, resultados de simulação típicos de m dependentes do tempo _z (componente perpendicular da magnetização da unidade) são mostrados na Fig. 1b. Se a interação RKKY for suficientemente forte (por exemplo, σ =1 × 10 ⁻³ J / m ² no caso A e no caso B), FL1 e FL2 estão acoplados e, portanto, suas dinâmicas de magnetização são quase idênticas, não importando se o DMI é considerado ou não. Observa-se também que a introdução do DMI distorce o processo de comutação da magnetização (ver caso B), o que está de acordo com os resultados relatados [21,22,23] e pode ser atribuído à troca antisimétrica do DMI. Uma vez que a interação RKKY não é forte o suficiente, a dinâmica de magnetização de FL1 e FL2 não pode ser idealmente acoplada de modo que uma diferença significativa entre eles seja observada (ver caso C). Abaixo, os resultados da simulação são obtidos sob uma interação RKKY suficientemente forte, a menos que indicado de outra forma.

Posteriormente, estudamos a velocidade de comutação sob as várias interações RKKY. A velocidade de comutação é refletida por um tempo quando m _z atinge 0 (definido como o tempo de comutação). O D ₁ e D ₂ são configurados com valores positivos e negativos, respectivamente [29]. Os resultados correspondentes são mostrados na Fig. 2. Na ausência de DMI, o tempo de comutação aumenta com a interação RKKY aprimorada, de acordo com os outros resultados relatados [26,27,28, 38]. A razão é que a interação RKKY mais forte torna a dinâmica de magnetização de FL1 e FL2 mais coerente, o que aumenta de forma equivalente a anisotropia da camada livre composta. No entanto, a dependência do tempo de comutação na força RKKY torna-se mais caótica na presença de DMI. Esse caos é atribuído principalmente à inconsistência da anisotropia entre FL1 e FL2. Mais explicações serão mostradas mais tarde. Esses resultados evidenciam o efeito não desprezível do DMI no comportamento de chaveamento do MTJ de interface dupla.

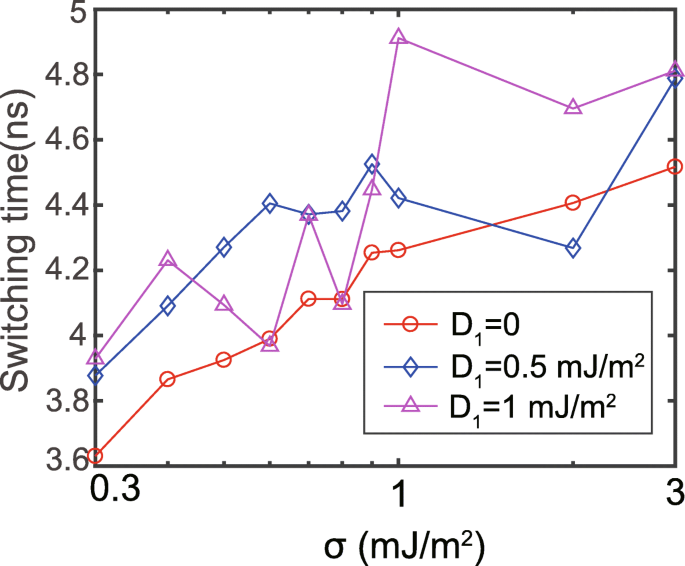
Tempo de comutação em função da força RKKY, com σ mostrado na escala logarítmica. D ₁ e D ₂ são definidos com os mesmos valores, mas com os sinais opostos

A seguir, estudamos o efeito do DMI em mais detalhes. A Figura 3 mostra o tempo de comutação em função da força do DMI. É importante mencionar que D ₁ e D ₂ são intencionalmente definidos com os mesmos valores positivos na Fig. 3a, embora tenham os sinais opostos na realidade. Em outras palavras, a Fig. 3a corresponde a um caso virtual, que estudamos para verificar o modelo de simulação. Do ponto de vista da teoria física, os efeitos prejudiciais de dois DMIs positivos são acumulados sob a ação da interação RKKY ferromagneticamente acoplada. Portanto, espera-se que o tempo de troca aumente com o aumento de D ₁ e D ₂ , conforme relatado em trabalhos anteriores [21, 22]. Esta análise está de acordo com os resultados mostrados na Fig. 3a. Assim, a racionalidade do modelo de simulação é validada. Em contraste com a Fig. 3a, os efeitos prejudiciais do DMI podem ser mitigados se D ₁ e D ₂ têm os sinais opostos, como mostrado na Fig. 3b, onde a variação do tempo de comutação é muito menor em comparação com a Fig. 3a. Observe que na Fig. 3b, a curva não é exatamente monótona, a flutuação local será explicada mais tarde. Notavelmente, os efeitos de DMIs em duas interfaces podem ser cancelados ajustando-se apropriadamente as magnitudes de D ₁ e D ₂ , conforme mostrado na Fig. 3c. Esses resultados podem ser explicados em termos de teorias de quiralidade como segue.

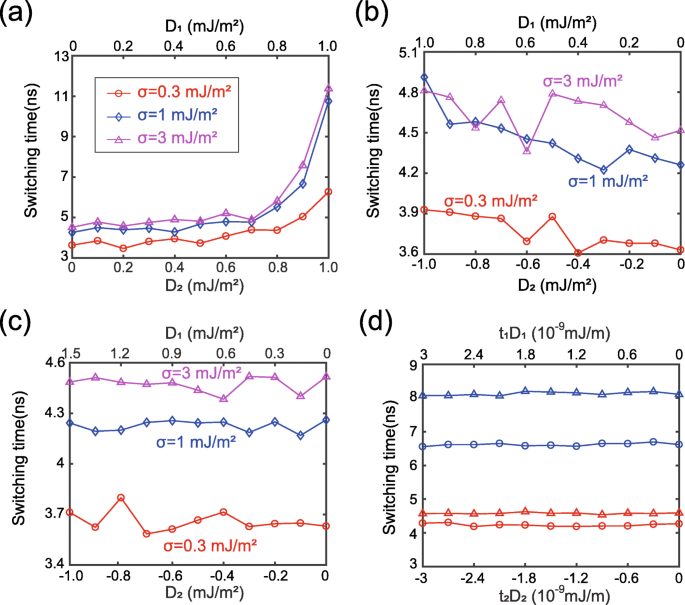
Tempo de comutação em função da força DMI. a D ₁ e D ₂ são definidos com o mesmo valor positivo. b D ₁ e D ₂ são definidos com o mesmo valor, mas com os sinais opostos. c D ₁ e D ₂ estão configurados para atender t ₁ D ₁ + t ₂ D ₂ =0. d Resultados adicionais ao alterar a espessura ou constante de anisotropia, enquanto mantém t ₁ D ₁ + t ₂ D ₂ =0. linha azul: t ₁ é alterado para 2 nm; linha vermelha: t ₁ é alterado para 1,5 nm. Dados do triângulo:σ =3 × 10 ⁻³ J / m ² . Dados do círculo:σ =1 × 10 ⁻³ J / m ²

A energia DMI é expressa como E _DM = t ∬ D [ m _x ( ∂m _z / ∂x ) - m _z ( ∂m _x / ∂x ) + m _y ( ∂m _z / ∂y ) - m _z ( ∂m _y / ∂y )] d ² r = tDε _DM [39], onde D é a constante DMI contínua, t é a espessura da camada ferromagnética. Como mencionado acima, a dinâmica de magnetização de FL1 e FL2 são quase idênticas sob uma interação RKKY suficientemente forte. Neste caso, o mesmo ε _DM é obtido em FL1 e FL2. Então, a energia DMI total de FL1 e FL2 pode ser calculada por E _tot =( t ₁ D ₁ + t ₂ D ₂ ) ε _DM . Portanto, definindo D ₁ / D ₂ =- t ₂ / t ₁ , os efeitos DMI de FL1 e FL2 poderiam ser completamente compensados no caso de um σ grande o suficiente, de acordo com a Fig. 3c. Esta conclusão é ainda verificada pelos resultados adicionais mostrados na Fig. 3d, onde os outros parâmetros são intencionalmente variados enquanto mantêm D ₁ / D ₂ =- t ₂ / t ₁ .

A magnitude DMI equivalente ( D _eq ) da camada livre composta pode ser expressa como D _eq =( t ₁ D ₁ + t ₂ D ₂ ) / ( t ₁ + t ₂ ), que pode ser usado para analisar quantitativamente o efeito do DMI no MTJ de interface dupla. Para validar a eficácia desta equação, mostramos dois grupos de resultados de simulação na Fig. 4a, onde duas curvas foram obtidas sob o mesmo D _eq mas com dois pares de diferentes { D ₁ , D ₂ } valores, respectivamente. Embora haja uma pequena diferença entre as duas curvas, suas tendências gerais são semelhantes e validam o efeito prejudicial do DMI na comutação STT. Aqui, a diferença entre duas curvas pode ser explicada da seguinte forma. FL1 e FL2 têm constantes de anisotropia diferentes, levando à oscilação incerta local da dinâmica de magnetização, conforme mostrado na Fig. 4c. O mesmo fenômeno também é observado nas Fig. 2 e Fig. 3b. Em vez disso, um caso ideal é mostrado na Fig. 4b, d, onde as constantes de anisotropia de FL1 e FL2 são definidas com os mesmos valores. Claramente, uma boa coincidência entre as duas curvas é vista, indicando que a expressão acima de D _eq poderia muito bem descrever o efeito DMI equivalente do MTJ de interface dupla.

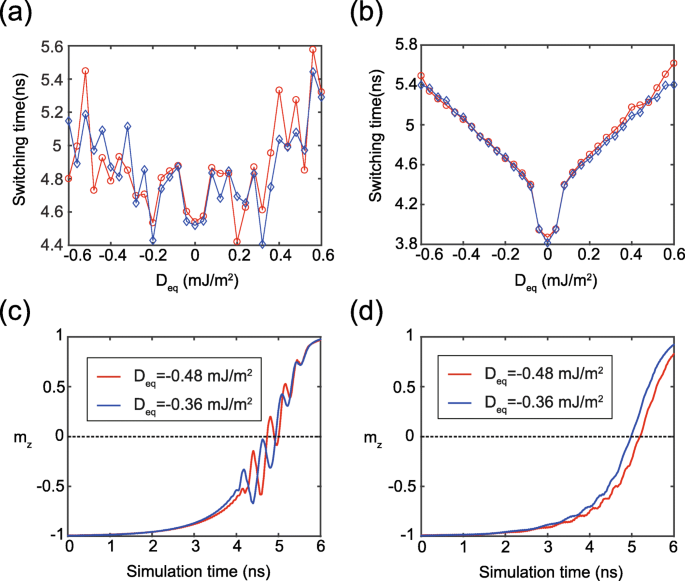
a , b Tempo de mudança em função de D _eq . Cada D _eq é obtido com dois pares de diferentes { D ₁ , D ₂ } valores de acordo com D _eq =( t ₁ D ₁ + t ₂ D ₂ ) / ( t ₁ + t ₂ ) Curva vermelha: D ₁ é variado entretanto D ₂ é fixado em 1 mJ / m ² . Curva azul: D ₁ e D ₂ são sempre definidos com o mesmo valor. Aqui, σ =1 × 10 ⁻² J / m ² . Em a , os demais parâmetros são configurados conforme Tabela 1. Em b , K _{u 1} = K _{u 2} =0,7 mJ / m ³ para um caso ideal. c , d Resultados típicos de m dependentes do tempo _z correspondendo a a e b , respectivamente

Finalmente, analisamos a evolução temporal da dinâmica da magnetização em mais detalhes. A Figura 5 mostra a energia dependente do tempo durante a comutação de magnetização. As energias DMI do FL1 e FL2 são acumuladas ou canceladas, dependendo dos sinais e magnitudes de D ₁ e D ₂ . Esta tendência está de acordo com os modelos teóricos acima. Além disso, as energias RKKY são mantidas em valores baixos, o que valida que os momentos magnéticos de FL1 e FL2 são acionados de forma síncrona. As distribuições dos campos RKKY e DMI são mostradas na Fig. 6, onde o campo RKKY desempenha papéis diferentes em vários casos. Em primeiro lugar, no caso de DMI diferente de zero (ver caso 2 e caso 3), o campo RKKY é muito mais forte em comparação com o caso de DMI zero (ver caso 1). Pode-se entender que o campo RKKY tem que superar a não uniformidade adicional das texturas magnéticas na presença de DMI. Em segundo lugar, se D ₁ e D ₂ são de sinais opostos, o campo RKKY resiste aos campos DMI em FL1 e FL2 (consulte o caso 2). Como resultado, o DMI é enfraquecido para que a dinâmica de magnetização se torne mais uniforme. Em contraste, uma vez D ₁ e D ₂ têm o mesmo sinal, o campo RKKY resiste ao campo DMI em uma camada ferromagnética, mas auxilia na outra camada ferromagnética (ver caso 3). Assim, o campo DMI geral ainda tem um certo efeito na dinâmica da magnetização, o que valida que o DMI não pode ser cancelado se D ₁ e D ₂ são do mesmo sinal.

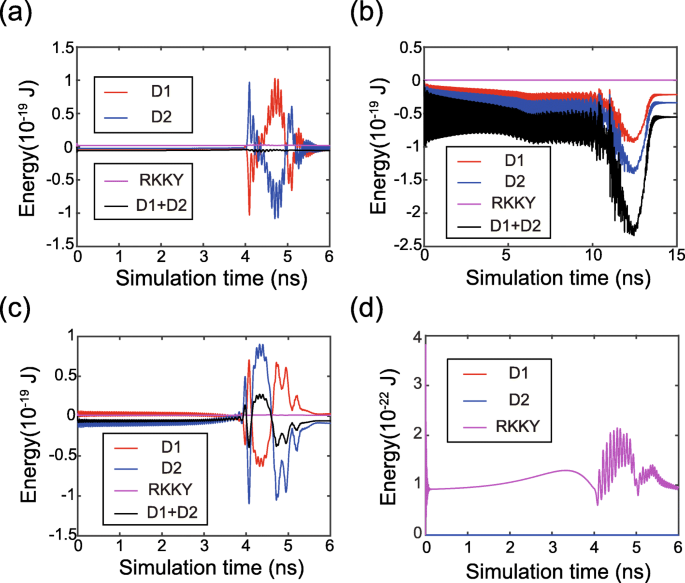
Evolução temporal das energias DMI e RKKY. a D ₁ =1,5 mJ / m ² , D ₂ =- 1 mJ / m ² , ou seja, o efeito DMI é cancelado. b D ₁ = D ₂ =1 mJ / m ² , isto é, o efeito DMI é acumulado. c D ₁ =1 mJ / m ² , D ₂ =- 1 mJ / m ² , ou seja, o efeito DMI é mitigado, mas não cancelado. d D ₁ = D ₂ =0

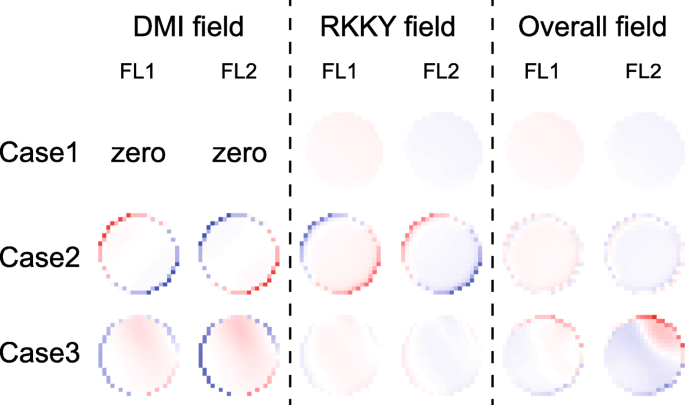
Distribuições espaciais dos campos DMI e RKKY. Aqui, um resultado típico em um determinado momento é mostrado para cada caso. A conclusão permanece inalterada nos outros momentos. Caso 1: D ₁ = D ₂ =0. Caso 2: D ₁ =1,5 mJ / m ² , D ₂ =- 1 mJ / m ² , ou seja, o efeito DMI é cancelado. Caso 3: D ₁ = D ₂ =1 mJ / m ² , ou seja, o efeito DMI é acumulado

A Figura 7 mostra as configurações micromagnéticas do FL1 e FL2 durante a comutação de magnetização. Embora a parede do domínio apareça em todos os casos, características diferentes podem ser observadas em alguns momentos. É bem sabido que o DMI favorece as texturas magnéticas não uniformes. No entanto, na Fig. 7, a magnetização uniforme ainda é formada, mesmo na presença de DMI (ver o tempo quando m _z =- 0,5 no caso 2), enquanto o efeito DMI for cancelado. Novamente, este resultado valida o modelo teórico acima. Além disso, também é visto que a dinâmica de magnetização é mais não uniforme se D ₁ e D ₂ são do mesmo sinal (ver caso 3 onde a parede do domínio sempre aparece), consistentes com a análise acima. Também mostramos alguns resultados simulados com MTJ menor (veja as duas últimas linhas na Fig. 7). A diferença de configurações micromagnéticas entre o caso 2 (DMI é cancelado) e o caso 3 (DMI não é cancelado) é mais notável.

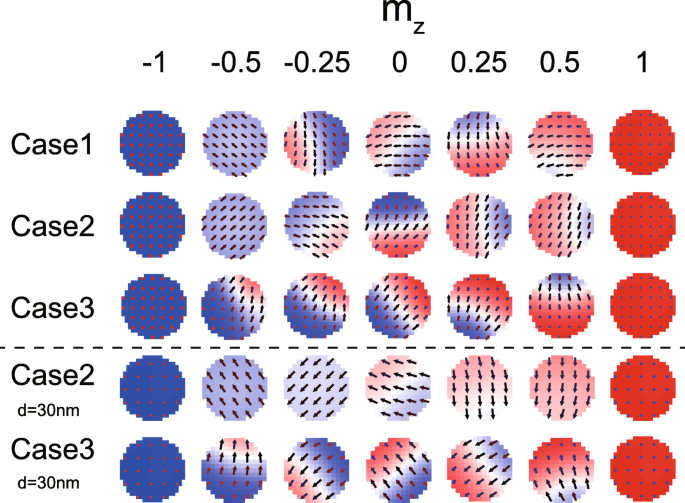
Configurações micromagnéticas durante a comutação de magnetização. Aqui, os casos 1 ~ 3 são configurados com os mesmos parâmetros da Fig. 6

Conclusão

Estudamos exaustivamente o efeito do DMI no STT-MTJ de interface dupla. Como é bem conhecido, o MTJ de interface dupla foi desenvolvido para aumentar a barreira de estabilidade térmica. Neste trabalho, nossos resultados comprovam outra vantagem do MTJ de interface dupla, ou seja, suprimir o efeito prejudicial do DMI. Os DMIs em duas camadas ferromagnéticas podem ser suprimidos ou mesmo cancelados se forem configurados com valores apropriados e sinais opostos, o que é naturalmente satisfeito pela estrutura STT-MTJ de interface dupla. Modelos teóricos foram propostos para explicar a conclusão. Os resultados da simulação micromagnética foram discutidos para revelar os papéis do DMI na dinâmica da magnetização. Nosso trabalho fornece uma abordagem viável para minimizar o DMI no STT-MTJ de interface dupla.

Disponibilidade de dados e materiais

Todos os dados estão totalmente disponíveis sem restrição.

Abreviações

DMI:: Interação Dzyaloshinskii-Moriya
FL:: Camada livre
FM / HM:: Ferromagneto / metal pesado
MRAM:: Memória magnética de acesso aleatório
MTJ:: Junção de túnel magnético
RKKY:: Ruderman – Kittel – Kasuya – Yosida
SOC:: Acoplamento spin-órbita
STT:: Torque de transferência de rotação

Nanopartículas de laminarina carregadas com protoporfirina IX para tratamento anticâncer, seu comportamento celular, detecção de ROS e estudos em animais Efeitos inibitórios sinergicamente aumentados da coadministração mediada por nanopartículas de pululana de lovastatina e doxorrubicina para células de câncer de mama triplo-negativas

Nanomateriais

Materiais Poliméricos

biológico

Corante

Especiarias