Grandes efeitos termoelétricos dependentes de spin em redes nanowire interconectadas baseadas em NiFe
Resumo
Liga de NiFe e redes de nanofios multicamadas (NW) de NiFe / Cu foram cultivadas usando um método de síntese eletroquímica assistida por modelo. As redes NW de liga de NiFe exibem grande energia termelétrica, que é amplamente preservada na atual geometria perpendicular ao plano da estrutura NW de várias camadas. Os efeitos da magneto-termelétrica gigante (MTP) foram demonstrados em NiFe / Cu NWs multicamadas com um valor de 25% a 300 K e atingindo 60% em torno de 100 K. Um grande coeficiente Seebeck dependente de spin de –12,3 μ V / K foi obtido à temperatura ambiente. Os grandes efeitos MTP demonstram uma abordagem magnética para controlar propriedades termoelétricas de dispositivos flexíveis baseados em redes NW.
Introdução
Os efeitos termoelétricos em materiais spintrônicos são ativamente estudados no campo emergente da caloritrônica de spin devido às suas propriedades físicas únicas, incluindo efeitos de Seebeck de spin, corrente de spin gerada termicamente e torque de transferência de spin assistido termicamente [1-7]. Além disso, os análogos termoelétricos dos efeitos magnetorresistivos em multicamadas magnéticas, válvulas de spin e junções de tunelamento, como os efeitos magneto-Seebeck gigante e magneto-Peltier, são de interesse especial, pois podem ser usados para permitir o controle magnético do fluxo de calor e termoelétrico tensões para recuperação de calor residual de circuitos eletrônicos [3, 8–13]. Os grandes efeitos termoelétricos dependentes de spin alcançados pela modificação adequada das configurações de magnetização da multicamada com um campo magnético externo exploram o fato de que os coeficientes de Seebeck para elétrons de spin up e spin down são significativamente diferentes. Esta diferença de coeficientes de Seebeck é atribuída à divisão de troca da banda d em metais ferromagnéticos de transição (FM), como sugerido em trabalhos anteriores realizados em ligas magnéticas diluídas [14, 15]. Ao considerar o efeito Peltier, isso significa que diferentes quantidades de calor são transportadas pelos elétrons de spin para cima e para baixo. Foi demonstrado recentemente que redes de nanofios magnéticos interconectados (NW) fabricados por deposição eletroquímica em filmes hospedeiros de polímeros nanoporosos 3D fornecem um caminho atraente para fabricar dispositivos caloritrônicos de spin leves, robustos, flexíveis e moldáveis em formatos versáteis que atendem aos principais requisitos para elétricos, térmicos e estabilidade mecânica [16, 17]. Além disso, a síntese eletroquímica é um método poderoso para a fabricação de nanofios multicomponentes com diferentes metais devido à sua simplicidade de engenharia, versatilidade e baixo custo [18-20]. Em tais redes de nanofios em escala centimétrica, a conectividade elétrica é essencial para permitir o fluxo de carga sobre todos os tamanhos de amostra. O sistema baseado em nanofios supera a falta de confiabilidade e reprodutibilidade dos resultados obtidos em nanopilares metálicos e junções de túnel magnético [3, 9, 10, 12], o que pode ser atribuído principalmente à resistência de contato térmico entre as amostras em nanoescala e o material térmico banhos que geram o gradiente de temperatura. As redes de nanofios 3D são promissoras para geradores termoelétricos flexíveis exibindo fator de potência termoelétrica magneticamente modulado e extremamente grande. Os módulos termoelétricos convencionais consistem em materiais termoelétricos tipo n e p acoplados ou pernas. Embora o trabalho inicial tenha se concentrado em sistemas NW tipo n feitos de multicamadas Co / Cu e CoNi / Cu [16, 17], foi recentemente demonstrado que ligas de NiCr diluídas são promissoras para a fabricação de pernas termoelétricas à base de nanofios tipo p [ 21]. No presente trabalho, relatamos resultados experimentais obtidos em outros filmes termoelétricos do tipo n baseados em Ni interconectado, ligas de NiFe e Ni 80 Fe 20 / Cu redes NW multicamadas. O níquel-ferro é um importante material magnético macio amplamente utilizado em tecnologias de armazenamento magnético de dados. Ligas de NiFe com composições de amostra otimizadas também exibem grande energia termelétrica perto da temperatura ambiente. Além disso, as multicamadas de NiFe / Cu são sistemas de magnetorresistência gigante (GMR) bem conhecidos [22]. A origem física do GMR são as diferentes propriedades de condução dos elétrons de spin majoritários e minoritários em multicamadas magnéticas. Através de medições de magneto-termelétricas e explorando o fato de que a arquitetura de nanofios ramificados dessas redes NW multicamadas permite medições elétricas na geometria da corrente perpendicular ao plano (CPP), uma determinação precisa dos coeficientes Seebeck dependentes de spin em permalloy (Ni 80 Fe 20 ) é obtido.
Métodos Experimentais
As membranas porosas de policarbonato (PC) com poros interconectados foram fabricadas expondo um 22- μ Filme de PC de espessura m para um processo de irradiação de duas etapas [23, 24]. A topologia das membranas foi definida expondo o filme a uma primeira etapa de irradiação em dois ângulos fixos de −25 ∘ e +25 ∘ em relação ao eixo normal do plano do filme. Depois de girar o filme do PC, no avião em 90 ∘ , a segunda etapa de irradiação ocorreu no mesmo fluxo de irradiação angular fixo para finalmente formar uma rede de nanocanais 3D. Em seguida, as trilhas latentes foram atacadas quimicamente seguindo um protocolo previamente relatado [25] para obter membranas porosas 3D com poros de 80 nm de diâmetro e porosidade volumétrica de 3%. Em seguida, os modelos de PC foram revestidos em um lado usando um evaporador de feixe eletrônico com uma bicamada metálica de Cr (3 nm) / Au (400 nm) para servir como cátodo durante a deposição eletroquímica. A rede NW preenche parcialmente a membrana 3D porosa do PC. NWs de liga de NiFe de composição controlada com teor de Fe abaixo de 40% foram cultivadas com sucesso em temperatura ambiente usando um banho de sulfato e depositando em diferentes potenciais [26]. Além disso, Py eletrodepositado (permalloy, Ni 80 Fe 20 ) / Nanofios multicamadas de Cu foram feitos de um banho de sulfato único contendo Ni 2+ , Fe 2+ e Cu 2+ íons usando uma técnica de eletrodeposição pulsada, conforme descrito na ref. [27]. Seguindo um procedimento descrito em outro lugar [18], as taxas de deposição de cada metal foram determinadas a partir do tempo de enchimento dos poros. A espessura das bicamadas foi fixada em 10 nm com aproximadamente a mesma espessura para as camadas Py e Cu. A impureza de cobre é incorporada apenas a um conteúdo muito limitado (menos de 5%) em permalloy, conforme avaliado por análise de energia dispersiva de raios-X (EDX). A microestrutura de nanofios simples de NiFe e NiFe / Cu crescidos por eletrodeposição em nanoporos foi previamente investigada usando difração de raios-X e microscopia eletrônica de transmissão analítica [28]. A Figura 1a ilustra a flexibilidade do filme do dispositivo caloritrônico de spin com base em uma rede de nanofios interconectada. O filme pode ser facilmente torcido sem danificar suas propriedades elétricas. A dissolução química do modelo de PC usando diclorometano leva a uma estrutura metálica interconectada autossustentável (inserção da Fig. 1a) que reproduz fielmente o modelo poroso 3D. Para a realização de medições de transporte elétrico e termoelétrico, o cátodo foi removido localmente por corrosão de plasma para criar um projeto de duas sondas adequado para medições elétricas como mostrado na Fig. 1b, c [16, 29, 30]. Nesta configuração, a corrente é injetada diretamente na estrutura ramificada do CNW (cerca de 1 cm de comprimento) a partir de seções não esticadas do cátodo metálico, onde os contatos elétricos são feitos diretamente por tinta Ag, e passa pelo 20- μ Rede NW de m de espessura graças ao alto grau de conectividade elétrica dos CNWs. Além disso, como o fluxo de correntes elétricas e térmicas é restrito ao longo dos segmentos de nanofios, a corrente flui perpendicularmente ao plano das camadas, no caso de uma estrutura multicamadas. Os valores de resistência típicos das amostras preparadas estão na faixa de algumas dezenas de ohms. Para cada amostra, a potência de entrada é mantida abaixo de 0,1 μ W para evitar o autoaquecimento, e a resistência foi medida dentro de sua faixa de resistência ôhmica com uma resolução de uma parte em 10 5 . O fluxo de calor é gerado por um elemento resistivo e uma tensão termoelétrica Δ V é criado pela diferença de temperatura Δ T entre os dois eletrodos metálicos. Os condutores de tensão eram feitos de fios finos de Chromel P, e a contribuição dos condutores para a energia termoelétrica medida foi subtraída usando os valores recomendados para a termopotência absoluta de Chromel P no banco de dados de termopares NIST ITS-90. O gradiente de temperatura foi monitorado com um termopar diferencial tipo E de pequeno diâmetro. Uma diferença típica de temperatura de 1 K foi usada nas medições. Para medições de magnetorresistência (MR) e magneto-termopotência (MTP), o campo magnético externo foi aplicado ao longo das direções fora do plano (OOP) e no plano (IP) dos filmes da rede NW (para mais detalhes, consulte as medições termoelétricas e fator de correção no arquivo adicional 1).
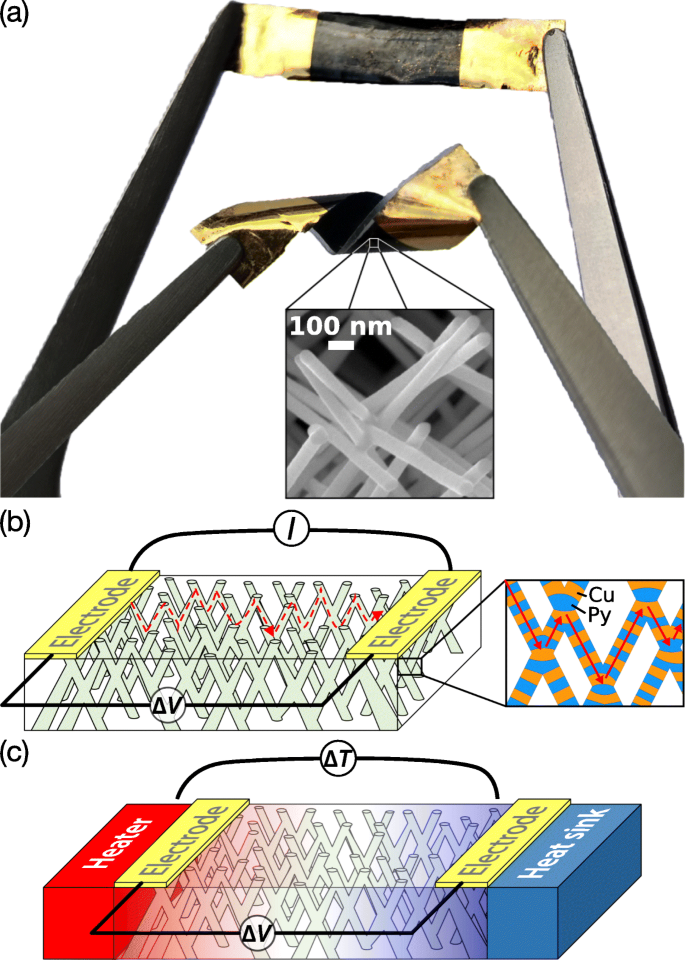
a Fotografia de um dispositivo caloritrônico de spin flexível baseado em uma rede de nanofios. A imagem SEM inserida mostra a estrutura ramificada de nanofios com diâmetro de ∼80 nm. Representação esquemática de um projeto de eletrodo para elétrica ( b ) e termoelétrica ( c ) medições de uma rede NW interconectada. A inserção da Fig. 1b mostra um desenho esquemático da estrutura de multicamadas Py / Cu. As setas vermelhas representam a direção do fluxo da corrente. A cor em c representa o perfil de temperatura gerado nas redes NW
Resultados e discussões
A energia termoelétrica absoluta em temperatura ambiente (RT) de redes NW de liga de Ni e NiFe puro contendo 20%, 30% e 40% de Fe é mostrada na Fig. 2a. A energia termelétrica aumenta continuamente com o aumento do teor de Fe, atingindo valores entre –20 μ V / K para Ni puro até cerca de –45 μ V / K para Ni 60 Fe 40 . As barras de erro da Fig. 2a são devidas às incertezas na composição das ligas relacionadas ao processo de galvanoplastia. Esses resultados estão de acordo com os dados experimentais obtidos em ligas de NiFe a granel [31]. Portanto, ligas de NiFe com composição de ajuste fino potencialmente rendem coeficientes Seebeck significativamente maiores do que metais ferromagnéticos puros como Co e materiais termopares como constantan (Cu 55 Ni 45 : S ≈ -38 μ V / K). Notamos também que o valor medido para Py NWs ( S ≈ -37 μ V / K) é muito semelhante aos valores de bulk relatados na literatura [32, 33]. Os painéis bec da Fig. 2 mostram as dependências do campo magnético RT da resistência e termopotência das redes Ni e Py NW com o campo aplicado nas direções IP e OOP. A resistência e a termopotência das amostras Py e Ni NW mostram as mesmas dependências do campo magnético ao longo das duas direções. O R ( H ) curvas correspondem bem ao efeito de magnetorresistência anisotrópica, que é devido à anisotropia de espalhamento spin-órbita em metais ferromagnéticos de transição. Este efeito leva a uma diminuição da resistividade à medida que o ângulo entre a magnetização e as direções da corrente é aumentado. De fato, o fluxo de corrente sendo restrito ao longo dos segmentos NW, a magnetização de saturação na direção IP faz um ângulo médio de ± 65 ∘ com a corrente. Em contraste, quando a magnetização está saturada na direção OOP, o ângulo médio entre a magnetização e o fluxo de corrente é muito menor (± 25 ∘ ) Portanto, a diminuição da resistência em um campo magnético aplicado externamente é aumentada quando o campo é aplicado na direção IP. Obviamente, o estado de resistência mais baixo esperado para a configuração perpendicular entre a magnetização e a corrente não poderia ser alcançado em tais redes NW. A observação de que o valor absoluto da termelétrica aumenta com o aumento do campo magnético transversal nas redes NW de liga de Ni e NiFe também está de acordo com estudos anteriores realizados em NWs individuais [34]. A Figura 2d mostra a magnitude da magnetorresistência e magneto-termopotência avaliada em RT na direção IP para redes NW de Ni puro e liga de NiFe. Aqui, as razões MR e MTP são definidas como MR =( R ( H =0) - R ( H sat )) / R ( H =0) e MTP =( S ( H =0) - S ( H sat )) / S ( H =0), com R ( H sat ) e S ( H sat ) a resistência e a energia termelétrica em H =10 kOe, respectivamente. Para as amostras de liga de NiFe, a magnitude da razão MTP é comparável ou menor (Py) à razão MR. Esse menor valor da razão MTP em relação à razão MR correspondente para a rede Py NW está de acordo com as medições realizadas em filmes finos de Py [35]. Em contraste, a rede Ni NW exibe um efeito MTP de –5% muito maior do que a razão MR de 1,5%. Este resultado está de acordo com as medições anteriores realizadas em Ni NWs únicos, mostrando o mesmo aumento do efeito MTP [34]. É interessante notar que para filmes finos de Ni, a anisotropia observada do coeficiente de Seebeck tem aproximadamente a mesma magnitude do que o MR anisotrópico (∼1,5%) [35]. Mais estudos são necessários para compreender este MTP aprimorado inesperado para Ni NWs.
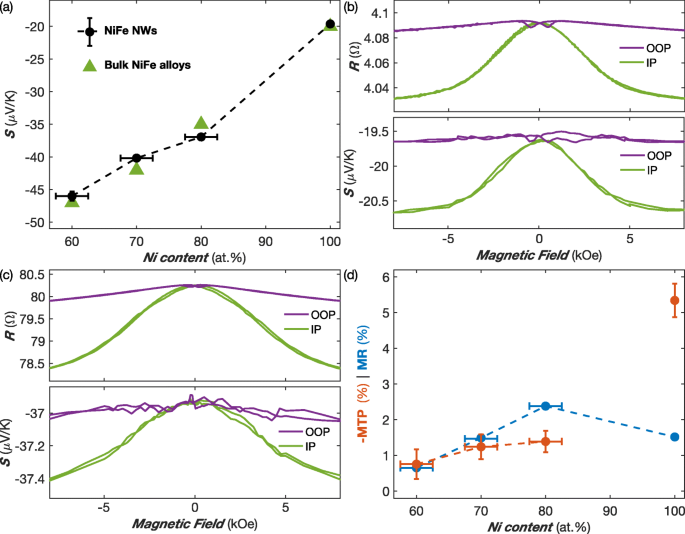
a Variação do coeficiente de Seebeck vs conteúdo de Ni em redes NiFe NW (diâmetro de 80 nm) à temperatura ambiente. Os valores recomendados para ligas a granel [38] também são relatados. b , c Variação da temperatura ambiente da resistência elétrica e coeficiente de Seebeck de Ni ( b ) e Py ( c ) Amostras NW obtidas com o campo aplicado no plano (IP) e fora do plano (OOP) do filme de rede NW. d Razões MR e MTP como uma função do conteúdo de Ni em redes NiFe NW no RT
Em multicamadas FM / Cu, o coeficiente Seebeck na direção perpendicular às camadas pode ser calculado a partir das propriedades de transporte correspondentes usando as regras de Kirchhoff [36],
$$ S _ {\ perp} =\ frac {S _ {\ text {Cu}} \ kappa _ {\ text {FM}} + \ lambda S _ {\ text {FM}} \ kappa _ {\ text {Cu}}} { \ lambda \ kappa _ {\ text {Cu}} + \ kappa _ {\ text {FM}}}, $$ (1)
onde S FM, Cu e κ FM, Cu representam a energia termelétrica e a condutividade térmica do material ferromagnético e Cu e λ = t FM / t Cu a proporção de espessura das camadas FM e Cu. De acordo com a Eq. 1, S ⊥ é determinado principalmente pela grande potência termelétrica do metal FM no caso da relação de espessura λ não é muito pequeno, pois S FM κ Cu >> S Cu κ FM .
Em contraste, o coeficiente de Seebeck de uma pilha de multicamadas FM / Cu na direção paralela às camadas é dado por
$$ S _ {\ parallel} =\ frac {S _ {\ text {Cu}} \ rho _ {\ text {FM}} + \ lambda S _ {\ text {FM}} \ rho _ {\ text {Cu}}} { \ lambda \ rho _ {\ text {Cu}} + \ rho _ {\ text {FM}}}, $$ (2)
com ρ FM e ρ Cu como as resistividades elétricas correspondentes. Neste caso, grande energia termelétrica pode ser obtida apenas no caso da relação de espessura λ é muito grande. O comportamento de contraste entre as direções paralelas e perpendiculares da camada é ilustrado na Fig. 3a para multicamadas Py / Cu usando as Eqs. 1 e 2, e a resistividade da literatura e valores de energia termelétrica para permalloy a granel [32, 33, 37, 38] ( ρ Py ≈ 25 μ Ω cm, S Py =–35 μ V / K) e cobre ( ρ Cu =1,6 μ Ω cm, S Cu =1,7 μ V / K), bem como as condutividades térmicas estimadas a partir da lei de Wiedemann-Franz ( κ ρ = L T , onde T é a temperatura e L é a proporção de Lorenz). Para o cristal único de Py em massa, a contribuição da rede relativamente pequena para a condutividade térmica deve mudar ligeiramente o valor estimado. Embora os valores de resistividade elétrica e condutividade térmica de nanofios de multicamadas possam variar consideravelmente de seus respectivos constituintes em massa, o mesmo comportamento de contraste entre as direções paralela e perpendicular das camadas permanece. Assim, NWs multicamadas com pilhas alternadas de materiais diferentes, como Py e Cu (ver Fig. 3a), são candidatos promissores para bons materiais termoelétricos.
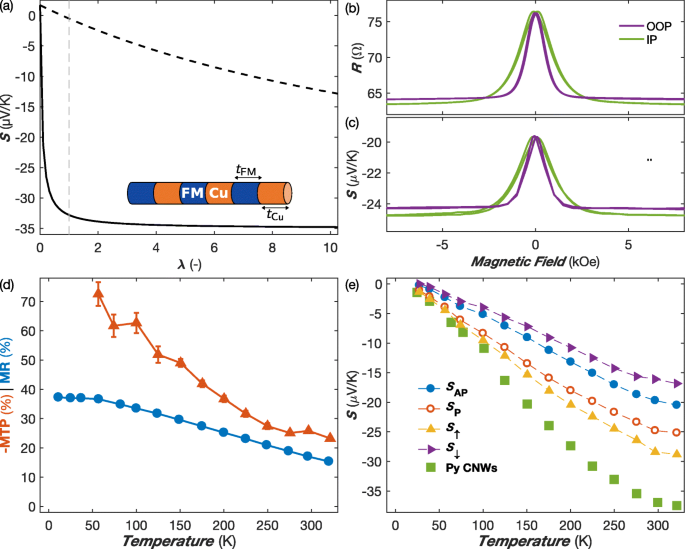
a Potência termelétrica calculada para multicamadas Py / Cu na camada paralela (linha tracejada) e perpendicular (linha sólida) direções vs relação espessura λ = t Py / t Cu usando Eqs. 1 e 2 e valores a granel para coeficientes de transporte. A linha tracejada cinza mostra os valores de λ =1; a inserção mostra uma pilha de multicamadas FM / Cu. b Variação da temperatura ambiente da resistência elétrica e coeficiente de Seebeck de uma rede Py / Cu NW em campos magnéticos aplicados nas direções IP e OOP. c Razão MR e MTP em função da temperatura com o campo aplicado no plano dos filmes da rede NW. d Coeficientes Seebeck medidos no campo zero aplicado S AP (círculos completos azuis) e no campo magnético de saturação S P (círculos abertos vermelhos), junto com o correspondente S calculado ↑ (triângulos laranja) e S ↓ (triângulos violetas) das Eqs. 5 e 6 (ver texto). Os dados obtidos em uma rede Py NW (diâmetro de 80 nm) também são relatados (quadrados verdes). As barras de erro refletem a incerteza das medições elétricas e de temperatura e são definidas para duas vezes o desvio padrão, reunindo 95% da variação dos dados
Conforme mostrado na Fig. 3b, a resistência e a energia termelétrica da rede Py / Cu NW mostram as mesmas dependências do campo magnético ao longo das direções OOP e IP do filme de rede NW. O eixo fácil está apontando ao longo da direção OOP, com um campo magnético de saturação de cerca de 1,8 kOe. Verificou-se que a amostra exibe grandes respostas de GMR (usando a definição atual da razão de GMR em que o efeito de MR é normalizado para o estado de resistência inferior R P , ou seja, GMR = R AP / R P -1, com R AP e R P como as resistências correspondentes nos estados de alta e baixa resistência) atingindo valores RT de 20,5% e 19% ao longo das direções IP e OOP, respectivamente. A pequena diferença é atribuída à contribuição da magnetorresistência anisotrópica. Como esperado, a energia termelétrica RT medida na rede CPP-GMR Py / Cu NW no estado saturado ( S ≈ –25 μ V / K ao longo da direção IP) é apenas ligeiramente menor do que o valor encontrado na amostra Py homogênea. Em contraste, os coeficientes RT Seebeck relatados para multicamadas NiFe / Cu na geometria CIP (∼-10 μ V / K) são muito menores [39]. A seguir, apenas as medidas obtidas no plano dos filmes da rede NW são relatadas. Conforme mostrado na Fig. 3c, o valor absoluto da magneto-termopotência MTP =( S AP - S P ) / S AP , com S AP e S P as termopares de difusão correspondentes nos estados de alta e baixa resistência, respectivamente, aumentam monotonicamente com a diminuição da temperatura de maneira semelhante à razão MR (definida como MR =( R AP - R P ) / R AP ) No entanto, enquanto a magnitude dos efeitos são semelhantes perto do RT, o MTP exibe um reforço pronunciado na faixa de baixa temperatura. Este comportamento está em contraste com o que tem sido observado nas redes Co / Cu e CoNi / Cu NW, que apresentam uma queda acentuada em seu MTP em baixas temperaturas [16, 17]. Perto de T =50 K, o MTP atinge cerca de 70% para a amostra Py / Cu, que é 2 a 3 vezes maior do que a das redes Co / Cu e CoNi / Cu NW. A proporção GMR em baixas temperaturas (∼60%) é apenas ligeiramente menor do que as relatadas anteriormente em matrizes de Py / Cu NWs paralelas [27, 40], demonstrando assim que filmes flexíveis CPP-GMR de alto desempenho baseados em redes NW podem ser fabricado por este método ascendente simples e barato.
Usando uma simples consideração dos caminhos paralelos de corrente de elétrons de spin-up e spin-down [41], as termopares correspondentes nos estados de alta e baixa resistência, S AP e S P , são simplesmente dados por:
$$ S _ {\ text {AP}} =\ frac {S _ {\ uparrow} \ rho _ {\ uparrow} + S _ {\ downarrow} \ rho _ {\ downarrow}} {\ rho _ {\ uparrow} + \ rho _ {\ downarrow}}, $$ (3)
e:
$$ S _ {\ mathrm {P}} =\ frac {S _ {\ uparrow} \ rho _ {\ downarrow} + S _ {\ downarrow} \ rho _ {\ uparrow}} {\ rho _ {\ uparrow} + \ rho _ {\ downarrow}}, $$ (4)
onde resistividades separadas ρ ↑ e ρ ↓ e coeficientes de Seebeck S ↑ e S ↓ são definidos para canais de spin majoritários e minoritários. Portanto, os coeficientes Seebeck dependentes de spin, S ↑ e S ↓ pode ser expresso da seguinte forma [16]:
$$ S _ {\ uparrow} =\ frac {1} {2} \ big [S _ {\ text {AP}} \ big (1- \ beta ^ {- 1} \ big) + S _ {\ mathrm {P} } \ big (1+ \ beta ^ {- 1} \ big) \ big], $$ (5) $$ S _ {\ downarrow} =\ frac {1} {2} \ big [S _ {\ text {AP }} \ big (1+ \ beta ^ {- 1} \ big) + S _ {\ mathrm {P}} \ big (1- \ beta ^ {- 1} \ big) \ big], $$ (6)
onde β =( ρ ↓ - ρ ↑ ) / ( ρ ↓ + ρ ↑ ) denota o coeficiente de assimetria de spin para resistividade. Uma estimativa aproximada de β =0,6 em baixas temperaturas usando β =MR 1/2 está de acordo com os resultados anteriores dos experimentos CPP-GMR realizados em multicamadas Py / Cu [42]. Das Eqs. 5 e 6, pode ser facilmente deduzido que S ↑ = S P e S ↓ = S AP no limite de uma razão MR extremamente grande ( β → 1). A Figura 3d mostra a evolução da temperatura de S AP , S P , S ↑ , e S ↓ . Abaixo de RT, os vários coeficientes de Seebeck diminuem quase que linearmente com a diminuição da temperatura, o que é indicativo da dominância da termelétrica de difusão. Os dados obtidos em uma rede homogênea Py NW também são mostrados na Fig. 3d para comparação. Para permalloy NWs, a magnitude do coeficiente de Seebeck é próxima à estimada para S ↑ , conforme esperado da Eq. 4. O valor RT para o coeficiente Seebeck dependente de spin Δ S = S ↑ - S ↓ de –12,3 μ V / K na rede Py / Cu NW é maior do que os obtidos anteriormente para Co / Cu e CoNi / Cu NWs [16, 17]. É também muito maior do que os estimados indiretamente a partir de medições realizadas na válvula nanopilar Py / Cu / Py e dispositivos de spin lateral usando um modelo de elementos finitos 3D [3, 11]. Nesses experimentos anteriores com nanoestruturas de Py / Cu, era difícil determinar e / ou eliminar a resistência térmica de contato, uma importante fonte de erro, e muitas vezes eram necessárias simulações para estimar o gradiente de temperatura sobre as pilhas multicamadas. Os coeficientes de Seebeck dependentes do spin da temperatura ambiente de diferentes sistemas de multicamadas magnéticas estão resumidos na Tabela 1. Em um trabalho anterior, foi sugerido que MTP infinitamente grande é esperado quando o produto β η tende a -1 [16]. A partir da análise acima, o produto β η próximo ao RT para nanofios Py / Cu é estimado próximo a –0,1, dando origem a magnitude semelhante de MTP e MR, como mostrado na Fig. 3d.
Conclusão
Em resumo, a síntese em larga escala de redes uniformes de nanofios de NiFe, liga de NiFe e Py / Cu multicamadas foi feita por eletrodeposição em modelos de polímero poroso 3D. Encontramos um valor inesperado alto de 5% para o MTP de Ni NWs em comparação com o MR (∼ 1,5%). As redes de nanofios de liga de NiFe exibem grande energia termelétrica, até cerca de - 45 μ V / K para Ni 60 Fe 40 à temperatura ambiente. Os Py / Cu NWs apresentam magnetorresistência gigante e efeitos magneto-termoelétricos na geometria perpendicular-ao-plano da corrente, que ultrapassa 50% em baixas temperaturas. Também encontramos um grande coeficiente de Seebeck dependente de spin de -12,3 μ V / K à temperatura ambiente, que é maior do que os valores relatados anteriormente em multicamadas magnéticas metálicas. Graças à facilidade de fabricar nanofios magnéticos de engenharia geométrica e multicamadas por eletrodeposição e suas excelentes propriedades elétricas e termoelétricas, essas redes 3D NW apresentam grande potencial para uso como dispositivos caloritrônicos de spin extremamente leves e flexíveis. Tais efeitos podem ser aplicados, por exemplo, usando e convertendo a energia do calor residual que ocorre em dispositivos eletrônicos ou, inversamente, para fornecer soluções de resfriamento ativo para dispositivos eletrônicos.
Disponibilidade de dados e materiais
Os conjuntos de dados usados e / ou analisados durante o estudo atual estão disponíveis junto ao autor correspondente, mediante solicitação razoável.
Nanomateriais
- Construção do Relé
- Eletromagnetismo
- Efeitos de circuito
- Transporte quântico torna-se balístico
- Nanodiamonds para sensores magnéticos
- Nanocluster para conduzir plasmons magnéticos
- Preparação e propriedades magnéticas de nanopartículas de espinélio FeMn2O4 dopadas com cobalto
- Magnetismo de Percolação em Nanopartículas Ferroelétricas
- Efeitos do pH microambiental do lipossoma na estabilidade química do fármaco carregado
- Efeitos de interação na montagem de nanopartículas magnéticas



