Efeitos de interação na montagem de nanopartículas magnéticas

Resumo

Uma taxa de absorção específica de um conjunto diluído de vários aglomerados aleatórios de nanopartículas de óxido de ferro em campo magnético alternado foi calculada usando a equação estocástica de Landau-Lifshitz. Esta abordagem leva em consideração simultaneamente a presença de flutuações térmicas dos momentos magnéticos das nanopartículas e a interação magneto-dipolo entre as nanopartículas dos aglomerados. É mostrado que para clusters 3D usuais, a intensidade da interação magneto-dipolo é determinada principalmente pela densidade de empacotamento do cluster η = N _p V / V _cl , onde N _p é o número médio de partículas no aglomerado, V é o volume da nanopartícula, e V _cl é o volume do cluster. A área do circuito de histerese de baixa frequência e a taxa de absorção específica do conjunto foram consideradas consideravelmente reduzidas quando a densidade de empacotamento dos aglomerados aumenta na faixa de 0,005 ≤ η <0,4. A dependência da taxa de absorção específica no diâmetro médio das nanopartículas é mantida com um aumento de η , mas se torna menos pronunciado. Para aglomerados fractais de nanopartículas, que surgem em meios biológicos, além de uma redução considerável da taxa de absorção, o máximo de absorção é deslocado para diâmetros de partícula menores. Verificou-se também que a taxa de absorção específica de aglomerados de fractais aumenta apreciavelmente com um aumento da espessura das camadas não magnéticas nas superfícies das nanopartículas.

Histórico

A hipertermia magnética [1,2,3,4] é uma das direções mais promissoras na pesquisa biomédica contemporânea relacionada ao tratamento do câncer. O desempenho das nanopartículas magnéticas para gerar calor em campo magnético externo alternado é afetado por vários fatores, como seus parâmetros geométricos e materiais, a concentração de nanopartículas na mídia, bem como a frequência e amplitude do campo magnético alternado. Neste artigo, o efeito da interação mútua magneto-dipolo na taxa de absorção específica (SAR) de um conjunto de nanopartículas magnéticas em um campo magnético alternado é estudado teoricamente. As nanopartículas de óxidos de ferro parecem mais promissoras para uso em hipertermia magnética [2,3,4,5], pois são biocompatíveis e biodegradáveis ​​e podem ser detectadas no corpo humano por meio de ressonância magnética clínica. Neste estudo, consideramos montagens de nanopartículas com parâmetros magnéticos típicos de nanopartículas de óxido de ferro. Foi descoberto recentemente [4, 6] que sendo incorporadas em um ambiente biológico, por exemplo, em um tumor, nanopartículas magnéticas acabam por ser fortemente ligadas aos tecidos circundantes. Portanto, a rotação das nanopartículas magnéticas como um todo sob a influência do campo magnético externo alternado é muito prejudicada. Nesse caso, o relaxamento browniano não é importante [4]. Portanto, apenas o movimento dos momentos magnéticos das partículas sob a influência de um campo magnético alternado e flutuações térmicas deve ser considerado. Além disso, deve-se levar em consideração a influência da interação dipolo magnético entre as partículas. O último efeito é especialmente importante uma vez que nanopartículas magnéticas em meios biológicos tendem a se aglomerar [2, 4, 7] formando agregados densos de nanopartículas com estrutura geométrica fractal [8, 9].

O efeito das flutuações térmicas na dissipação de calor em um conjunto diluído de nanopartículas magnéticas em campo magnético alternado foi estudado em detalhes nas Refs. [10,11,12,13]. Em particular, foi demonstrado [10] que o SAR de tal montagem depende substancialmente do diâmetro médio das nanopartículas, entre outros fatores. Para uma montagem de nanopartículas diluídas, cálculos detalhados [10] permitem determinar o diâmetro ideal das nanopartículas nos parâmetros magnéticos de partícula dados e dada amplitude e frequência do campo magnético alternado. Com a escolha ideal dos parâmetros geométricos e magnéticos das nanopartículas, valores de SAR muito elevados, da ordem de 1000 kW / kg, foram previstos [10, 11]. É notável que os valores de SAR relatados em uma série de experimentos [14,15,16,17] estão realmente próximos das estimativas teóricas acima. Ao mesmo tempo, em muitos experimentos [5, 18,19,20,21] foram medidos valores significativamente mais baixos de SAR ~ 20–50 kW / kg. Este fato pode ser explicado, provavelmente, pela influência da forte interação magneto-dipolo em densas montagens de nanopartículas magnéticas.

Na verdade, foi experimentalmente mostrado [22, 23] que o SAR na montagem densa de nanopartículas magnéticas depende essencialmente da razão de aspecto da amostra de teste, ou seja, a razão entre o comprimento e a largura da amostra. Esta é uma evidência indireta da influência da interação magneto-dipolo na resposta de um conjunto de nanopartículas em um campo magnético externo alternado. O efeito da interação magneto-dipolo na taxa de absorção de energia pela montagem de nanopartículas magnéticas tem sido estudado em uma série de investigações teóricas e experimentais recentes [7, 24,25,26,27,28,29,30,31,32 , 33,34,35,36,37,38]. No entanto, novas investigações parecem necessárias para levar em conta a natureza fractal [8, 9] da distribuição das nanopartículas em meios biológicos.

Para ver claramente o efeito da interação magneto-dipolo, neste artigo, primeiro calculamos o SAR de uma montagem de nanopartículas de óxido de ferro não interagentes. Para estudar o efeito da interação magneto-dipolo, resolvemos numericamente a equação estocástica de Landau-Lifshitz [13, 39,40,41], que leva em consideração simultaneamente a presença de flutuações térmicas dos momentos magnéticos das partículas e a interação magneto-dipolo entre as nanopartículas dos clusters. Dois tipos de aglomerados magnéticos são considerados, os usuais aglomerados 3D aleatórios de nanopartículas distribuídas em uma mídia rígida e os aglomerados fractais de nanopartículas que geralmente surgem no espaço intracelular. Observe que, dentro do cluster, as nanopartículas são acopladas por uma forte interação magneto-dipolo. Ao mesmo tempo, para uma montagem diluída de aglomerados, a interação magnética entre os aglomerados pode ser desprezada em uma primeira aproximação.

A influência da interação magneto-dipolo nas propriedades de uma montagem diluída de aglomerados 3D aleatórios é mostrada como sendo determinada principalmente pela densidade de empacotamento de nanopartículas η = N _p V / V _cl , onde N _p é o número médio de partículas no aglomerado, V é o volume da nanopartícula, e V _cl é o volume do cluster. A área do loop de histerese e o SAR de montagem são considerados reduzidos consideravelmente quando a densidade de empacotamento dos clusters 3D aumenta na faixa de densidades de empacotamento estudada, 0,005 ≤ η <0,4. Para aglomerados fractais de nanopartículas magnéticas, além da redução considerável do SAR, a taxa de absorção máxima é deslocada para diâmetros de partícula menores, como regra. Verificou-se também que o SAR de aglomerados fractais aumenta apreciavelmente com o aumento da espessura das camadas não magnéticas nas superfícies das nanopartículas. Este efeito pode ser importante para a aplicação de montagens de nanopartículas magnéticas em hipertermia magnética.

Simulação Numérica

Nanopartículas sem interação

É instrutivo lembrar primeiro o comportamento de uma montagem de nanopartículas superparamagnéticas não interagentes em um campo magnético alternado. Permite ver claramente a influência da interação magneto-dipolo nas propriedades da montagem. Com base na equação de Fokker-Planck derivada de W.F. Brown [39], pode-se obter uma equação cinética aproximada [10] para os números da população n ₁ ( t ) e n ₂ ( t ) de dois poços de potencial de nanopartícula superparamagnética uniaxial
$$ \ frac {\ parcial {n} _1} {\ parcial t} =\ frac {n_2} {\ tau_2 (T)} - \ frac {n_1} {\ tau_1 (T)}; \ kern2em {n} _1 (t) + {n} _2 (t) =1. $$ (1)
Aqui, τ ₁ ( T ) e τ ₂ ( T ) são os tempos de relaxamento correspondentes a uma determinada temperatura T para o primeiro e segundo poços de potencial, respectivamente. Os tempos de relaxamento τ ₁ ( T ) e τ ₂ ( T ) dependem essencialmente da amplitude e direção do campo magnético aplicado em relação ao eixo de anisotropia fácil de partículas (ver Apêndice na Ref. [10]). O procedimento de iteração pode ser usado para calcular os números da população de poços n ₁ ( t ) e n ₂ ( t ) por vários períodos do campo magnético alternado. É suficiente obter um ciclo de histerese estacionário de uma partícula em um campo magnético alternado. Para fazer isso, pode-se usar uma relação aproximada para o componente da magnetização de partículas reduzida ao longo da direção do campo magnético
$$ \ frac {M_h} {M_sV} ={m} _h (t) ={n} _2 (t) \ cos \ left [{\ theta} _0 - {\ theta} _ {\ min, 2} \ left ({h} _e (t) \ right) \ right] + {n} _1 (t) \ cos \ left [{\ theta} _0 - {\ theta} _ {\ min, 1} \ left ({h} _e (t) \ right) \ right] $$ (2)
Aqui, θ ₀ é o ângulo do campo magnético externo em relação ao eixo de anisotropia fácil de partículas, θ _{min, 1} e θ _{min, 2} são as localizações dos mínimos do poço potencial como as funções do campo magnético aplicado reduzido, h _e ( t ) = H ₀ pecado ( ωt ) / H _a , onde ω =2π f é a frequência angular, H _a sendo o campo de anisotropia de partículas. Para obter um ciclo de histerese de uma montagem de nanopartículas independentes orientadas aleatoriamente, é necessário calcular a média da magnetização reduzida m _h ( t ) sobre as direções do campo magnético. É importante notar que a precisão de uma solução analítica aproximada, Eq. (1), (2), da equação de Fokker-Planck foi validada [10] por meio de comparação direta com as soluções numéricas da equação estocástica de Landau-Lifshitz para nanopartículas magnéticas não interagentes.

Aglomerados de nanopartículas

Para investigar o efeito da interação magneto-dipolo na taxa de absorção específica de um conjunto de nanopartículas magnéticas interagindo em um campo magnético alternado, neste artigo, estudamos o comportamento de uma montagem diluída de aglomerados 3D usuais de nanopartículas superparamagnéticas e de fractal clusters [8, 9] que surgem geralmente em meios biológicos carregados com nanopartículas magnéticas finas.

Um agrupamento quase esférico 3D de nanopartículas mostrado esquematicamente na Fig. 1a pode ser caracterizado por seu raio R _cl , e o número de nanopartículas, N _p >> 1, dentro do seu volume. Presume-se que as nanopartículas têm quase o mesmo diâmetro D , e seus centros, { r _i }, i =1, 2, .. N _p , são distribuídos aleatoriamente no volume do cluster. Também assumimos que as partículas são revestidas com camadas não magnéticas finas, de forma que a interação de troca entre as nanopartículas vizinhas do cluster está ausente. Como mencionamos acima, tal cluster 3D é caracterizado pela densidade de empacotamento de nanopartículas η = N _p V / V _cl . Este é o volume total do material magnético distribuído no volume do cluster. Pode-se definir a distância média entre as nanopartículas do cluster por meio da relação D _av =(6 V _cl / πN _p ) ^1/3 . Então, a densidade de empacotamento das nanopartículas é dada por η =( D / D _av ) ³ .

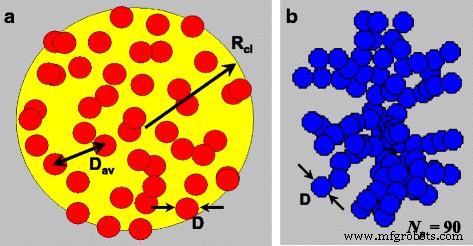
Geometria de cluster 3D quase esférico aleatório de nanopartículas de domínio único ( a ) e cluster fractal ( b ) com descritores fractais D _f =2.1 e k _f =1,3

Para uma montagem de clusters 3D completamente aleatórios, as orientações dos eixos de fácil anisotropia das nanopartículas { e _i }, i =1, 2, .. N _p , são escolhidos aleatoriamente e independentemente na esfera unitária. Alternativamente, pode-se supor que durante a formação de aglomerados em uma solução sob a influência da interação magneto-estática, certa correlação ocorre na distribuição das direções do eixo de anisotropia fácil das nanopartículas. Uma possibilidade para descrever tais aglomerados parcialmente ordenados é assumir que os eixos de anisotropia fácil das nanopartículas estão uniformemente distribuídos em um ângulo sólido, θ < θ _max , nas coordenadas esféricas.

Clusters 3D aleatórios com um determinado número de partículas N _p de diâmetro D foram criados neste estudo da seguinte forma. Primeiro, geramos um conjunto denso e aproximadamente uniforme de N pontos aleatórios { ρ _i } dentro de um volume esférico do raio R _cl , de modo que | ρ _i | ≤ R _cl para todos os pontos gerados, i =1, 2 ... N , N >> N _p . O centro da primeira nanopartícula foi colocado no primeiro ponto aleatório, r ₁ = ρ ₁ . Então, todos os pontos aleatórios com coordenadas | ρ _i - r ₁ | ≤ D foram removidos do conjunto inicial de pontos aleatórios. Após esta operação, qualquer ponto no conjunto restante de pontos aleatórios pode ser usado como um centro da segunda nanopartícula. Por exemplo, pode-se colocar simplesmente r ₂ = ρ ₂ . Na próxima etapa, remove-se todos os pontos aleatórios cujas coordenadas satisfaçam a desigualdade | ρ _i - r ₂ | ≤ D . Este procedimento é repetido até que todos os N _p centros de nanopartículas são colocados dentro do volume do cluster. Como resultado, todos os centros de nanopartículas aleatórios estão dentro de uma esfera de raio R _cl , de modo que | r _i | ≤ R _cl , eu =1, 2, ... N _p . Além disso, nenhuma das nanopartículas está em contato direto com as nanopartículas vizinhas. Este algoritmo permite construir grupos 3D quase esféricos aleatórios de nanopartículas magnéticas para valores moderados da fração de volume das nanopartículas η <0,5.

Para um determinado conjunto de parâmetros iniciais, ou seja, D , R _cl , e N _p , vários clusters 3D aleatórios diferem pelos conjuntos de coordenadas dos centros das nanopartículas { r _i } e orientações { e _i } dos eixos de anisotropia fácil de partículas. No entanto, os cálculos mostram que no limite N _p >> 1, os loops de histerese obtidos para diferentes realizações de variáveis ​​aleatórias { r _i } e { e _i } diferem apenas ligeiramente um do outro. Para caracterizar o comportamento de uma montagem diluída de aglomerados aleatórios de nanopartículas, é necessário calcular o loop de histerese de montagem em média sobre um número suficientemente grande de realizações de cluster aleatórias. Verifica-se que no limite N _p >> 1, o ciclo de histerese média da montagem do cluster tem uma dispersão bastante pequena, mesmo sendo calculada em média sobre 20-30 realizações independentes de clusters aleatórios com os valores fixos dos parâmetros iniciais D , R _cl , e N _p .

A geometria dos clusters fractais de nanopartículas de domínio único é caracterizada [42, 43] pelos descritores fractais D _f e k _f . Por definição, o número total de nanopartículas N _p no cluster fractal é dado pela relação \ ({N} _p ={k} _f {\ left (2 {R} _g / D \ right)} ^ {D_f} \), onde D _f é a dimensão fractal, k _f é o prefator fractal, e R _g sendo o raio de giração. É definido [43] através do quadrado médio das distâncias entre os centros das partículas e o centro geométrico de massa do agregado. Neste artigo, os clusters fractais com vários descritores fractais foram criados usando o conhecido algoritmo de Filippov et al. [43]. Como exemplo, a Fig. 1b mostra a estrutura geométrica do aglomerado fractal com descritores fractais D _f =2.1 e k _f =1,3 consistindo em N _p =90 nanopartículas de domínio único. Geometricamente, parece que a principal diferença entre os clusters 3D e fractais é que, no último caso, cada nanopartícula tem pelo menos um vizinho localizado na distância mais próxima possível entre os centros das nanopartículas igual ao diâmetro da nanopartícula D .

Dinâmica do vetor de magnetização unitária \ ({\ overrightarrow {\ alpha}} _ i \) de i -ésima nanopartícula de domínio único do cluster é determinada pela equação estocástica de Landau-Lifshitz (LL)
$$ \ frac {\ partial {\ overrightarrow {\ alpha}} _ i} {\ partial t} =- {\ gamma} _1 {\ overrightarrow {\ alpha}} _ i \ times \ left ({\ overrightarrow {H}} _ {ef, i} + {\ overrightarrow {H}} _ {th, i} \ right) - {\ kappa \ gamma} _1 {\ overrightarrow {\ alpha}} _ i \ times \ left ({\ overrightarrow {\ alpha}} _ i \ times \ left ({\ overrightarrow {H}} _ {ef, i} + {\ overrightarrow {H}} _ {th, i} \ right) \ right), $$ (3)
onde γ é a razão giromagnética, κ is phenomenological damping parameter, γ ₁  = γ /(1+κ ² ), \( {\overrightarrow{H}}_{ef,i} \) is the effective magnetic field and \( {\overrightarrow{H}}_{th,i} \) is the thermal field. The effective magnetic field acting on a separate nanoparticle can be calculated as a derivative of the total cluster energy
$$ {\overrightarrow{H}}_{ef,i}=-\frac{\partial W}{VM_s\partial {\overrightarrow{\alpha}}_i}. $$ (4)
The total magnetic energy of the cluster W  = W _a  + W _Z  + W _m is a sum of the magneto-crystalline anisotropy energy W _a , Zeeman energy W _Z of the particles in applied magnetic field \( {\overrightarrow{H}}_0\sin \left(\omega t\right) \), and the energy of mutual magneto-dipole interaction of the particles W _m .

For nanoparticles of nearly spherical shape with uniaxial type of magnetic anisotropy the magneto-crystalline anisotropy energy is given by
$$ {W}_a=KV\sum \limits_{i=1}^{N_p}\left(1-{\left({\overrightarrow{\alpha}}_i{\overrightarrow{e}}_i\right)}^2\right), $$ (5)
where e _i is the orientation of the easy anisotropy axis of i -th particle of the cluster. Zeeman energy W _Z of the cluster in applied magnetic field is given by
$$ {W}_Z=-{M}_sV\sum \limits_{i=1}^{N_p}\left({\overrightarrow{\alpha}}_i{\overrightarrow{H}}_0\sin \left(\omega t\right)\right). $$ (6)
Next, for spherical uniformly magnetized nanoparticles, the magneto-static energy of the cluster can be represented as the energy of the point interacting dipoles located at the particle centers r _i dentro do cluster. Then, the magneto-dipole interacting energy is
$$ {W}_m=\frac{M_s^2{V}^2}{2}\sum \limits_{i\ne j}\frac{{\overrightarrow{\alpha}}_i{\overrightarrow{\alpha}}_j-3\left({\overrightarrow{\alpha}}_i{\overrightarrow{n}}_{ij}\right)\left({\overrightarrow{\alpha}}_j{\overrightarrow{n}}_{ij}\right)}{{\left|{\overrightarrow{r}}_i-{\overrightarrow{r}}_j\right|}^3}, $$ (7)
where n _ij is the unit vector along the line connecting the centers of i -th and j -th particles, respectively.

Thus, the effective magnetic field acting on the i -th nanoparticle of the cluster is given by
$$ {\overrightarrow{H}}_{ef,i}={H}_a\left({\overrightarrow{\alpha}}_i{\overrightarrow{e}}_i\right){\overrightarrow{e}}_i+{\overrightarrow{H}}_0\sin \left(\omega t\right)+{M}_sV\sum \limits_{j\ne i}\frac{{\overrightarrow{\alpha}}_j-3\left({\overrightarrow{\alpha}}_j{\overrightarrow{n}}_{ij}\right){\overrightarrow{n}}_{ij}}{{\left|{\overrightarrow{r}}_i-{\overrightarrow{r}}_j\right|}^3}. $$ (8)
where H _a  = 2 K /M _s. is the particle anisotropy field.

The thermal fields, \( {\overrightarrow{H}}_{th,i} \), i  = 1, 2...N _p , acting on various nanoparticles of the cluster are statistically independent, with the following statistical properties [39] of their components for every nanoparticle
$$ \left\langle {H}_{th}^{\left(\alpha \right)}(t)\right\rangle =0;\left\langle {H}_{th}^{\left(\alpha \right)}(t){H}_{th}^{\left(\beta \right)}\left({t}_1\right)\right\rangle =\frac{2{k}_B T\kappa}{\gamma {M}_sV}{\delta}_{\alpha \beta}\delta \left(t-{t}_1\right),\alpha, \beta =\left(x,y,z\right). $$ (9)
Here, k _B is the Boltzmann constant, δ _αβ is the Kroneker symbol, and δ (t ) is the delta function.

The procedure for solving stochastic differential Eqs. (3), (8), and (9) is described in detail in Refs. [13, 40, 41].

Resultados e discussão

Non-Interacting Iron Oxide Nanoparticles

Consider a dilute assembly of superparamagnetic nanoparticles with an average diameter D . The particles are assumed to be tightly packed in a surrounding media, and their easy anisotropy axes are randomly oriented in space. The hysteresis loop of such an assembly in an alternating magnetic field H  = H ₀ sin(ωt ) can be calculated [10] using Eqs. (1) and (2). This approach, due to its simplicity, allows one to carry out detailed calculations of the assembly hysteresis loops for various particle sizes depending on frequency and amplitude of the alternating magnetic field. In the calculations performed, in accordance with the experimental data [2,3,4,5,6], the saturation magnetization of iron oxide nanoparticles is assumed to be M _s.  = 70 Am ² /kg, the magnetic anisotropy constant being K  = 10 ⁴  J/m ³ . The assembly temperature is T  = 300 K, and the nanoparticle diameters are in the range D  = 10–30 nm. These parameters seem typical for experiments carried out on iron oxide nanoparticles.

Figure 2 shows the SAR of non-interacting assemblies of iron oxide nanoparticles at various frequencies at a fixed amplitude of alternating magnetic field, H ₀  = 8 kA/m. As can be seen, for the range of frequencies that are characteristic for magnetic hyperthermia, f  = 200–500 kHz, SAR has a maximum for the assembly of iron oxide nanoparticles with diameters D  = 20–21 nm. It is notable that even at relatively moderate amplitude of an alternating magnetic field, the assembly SAR reaches sufficiently high values, 350–450 kW/kg, if the nanoparticle diameters are chosen properly.

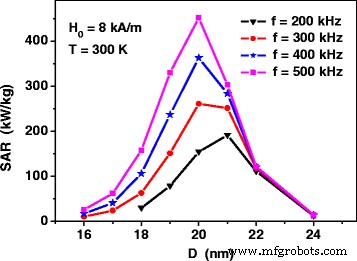
The specific absorption rate of non-interacting assembly of iron oxides nanoparticles, obtained by means of Eqs. (1) and (2), as a function of average particle diameter at different frequencies of the alternating magnetic field

However, the experimentally measured SAR values for assemblies of iron oxides nanoparticles are, as a rule, significantly below [18,19,20,21] these theoretical values. As we shall see in the next section, this fact can be explained [22,23,24,25,26,27,28,29,30,31,32,33,34,35,36,37,38] by the influence of strong magneto-dipole interaction in dense assemblies of magnetic nanoparticles.

Assembly of 3D Clusters

Consider now the hysteresis loops of a dilute assembly of 3D random clusters having easy anisotropy axes of individual nanoparticles randomly oriented in space. As Fig. 2 shows, for the assembly of non-interacting iron oxide nanoparticles, the peak of the energy absorption in an alternating magnetic field corresponds to particles with diameter D  = 20 nm. Therefore, first we calculated the hysteresis loops of an assembly of 3D clusters with particle diameter D  = 20 nm.

Figure 3a shows the evolution of the assembly hysteresis loops depending on the average distance between the nanoparticle centers D _av at the fixed value of the particle diameter D . The frequency and amplitude of alternating magnetic field are fixed at f  = 400 kHz and H ₀  = 8 kA/m, respectively. The number of particles in the clusters equals N _p  = 40. The calculations are carried out at T  = 300 K, and magnetic damping constant is taken to be κ  = 0.5.

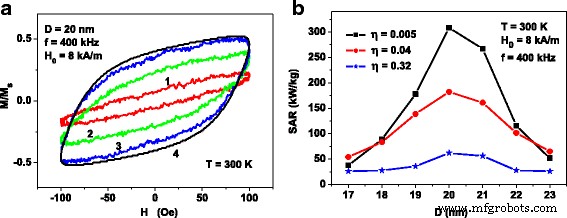
(a ) Evolution of the hysteresis loops of dilute assembly of clusters of iron oxide nanoparticles with diameter D  = 20 nm for various ratios D _av /D :(1 ) D _av /D  = 1.46; (2 ) D _av /D  = 2.92; (3 ) D _av /D  = 5.84. Hysteresis loop 4 corresponds to assembly of non-interacting nanoparticles of the same diameter. It is calculated by means of Eqs. (1) and (2). (b ) SAR as a function of the average nanoparticle diameter D for dilute assemblies of clusters of nanoparticles with different packing density η

Evidently, the decrease of the average distance between the nanoparticles of the cluster leads to an increase of intensity of the magneto-dipole interaction within the cluster. Note that for N _p  = 40, the ratios D _av /D specified in Fig. 3a correspond to the cluster packing densities η  = 0.005, 0.04, and 0.32, correspondingly. One can see in Fig. 3a that the hysteresis loop area rapidly decreases as a function of the parameter η . For comparison, Fig. 3a also shows the hysteresis loop 4, calculated for an assembly of non-interacting particles, i.e., in the limit D _av /D → ∞, N _p  = const, using Eqs. (1) and (2).

One can see that the hysteresis loop 3 (η  = 0.005) in Fig. 3a turns out to be close to the hysteresis loop of the assembly of non-interacting nanoparticles. Therefore, in the case η  ≤ 0.005 the magneto-dipole interaction of the nanoparticles within the cluster can be neglected. However, for η  ≥ 0.04 the magneto-dipole interaction has a significant influence on the properties of an assembly of random 3D clusters. A similar evolution of the assembly hysteresis loops has been obtained also for the frequencies f  = 300 and 500 kHz, respectively.

The hysteresis loops shown in Fig. 3a are calculated for different ratios D _av /D , but for the fixed number of nanoparticles in the cluster N _p  = 40. However, the detailed computer simulations show that the shape of the hysteresis loop of a dilute assembly of random 3D clusters is practically unchanged, if the number of particles, N _p  >> 1, and the radius of the cluster R _cl are changed so that the nanoparticle packing density η remains constant. Therefore, the hysteresis loop of dilute assembly of random 3D clusters depends mainly on the cluster packing density η .

Figure 3b shows the SAR of assemblies of random clusters of iron oxide nanoparticles for different η valores. The SAR of the assembly is calculated [10] as SAR  = M _s fA /ρ , where A is the hysteresis loop area in the variables (M /M _s. , H ), ρ being the density of iron oxide nanoparticles which is assumed to be ρ  = 5 × 10 ³  kg/m ³ . As Fig. 3b shows, the SAR decreases as a function of η due to an increase of the intensity of magneto-dipole interaction within the clusters. At the same time, the dependence of the assembly SAR on the average particle diameter still remains, though it becomes less pronounced.

For small values of η  ≤ 0.005, the SAR of random assembly of 3D clusters actually coincides with that one for an assembly of non-interacting nanoparticles, shown in Fig. 2. On the other hand, SAR falls about six times when the cluster packing density increases up to η  = 0.32. Then, it becomes close to typical SAR values ~ 50–100 kW/kg, which are obtained in a number of experiments [5, 18,19,20,21] with iron oxide nanoparticle assemblies.

Assembly of Fractal Clusters

Similar calculations were carried out for dilute assemblies of fractal clusters of nanoparticles with various fractal descriptors. As Fig. 4 shows, for fractal clusters of nanoparticles, the SAR as a function of the particle diameter also decreases considerably with respect to that of the assembly of non-interacting nanoparticles. However, in contrast to the assembly of 3D clusters, the peak values of SAR are shifted systematically to smaller particle diameters, except for the case of fractal dimension D _f  = 2.7, which is close to the case of 3D clusters with D _f  = 3.0. It is interesting to note also that for non-optimal nanoparticle diameters, for example, for nanoparticles with diameters D  ≤ 17 nm, the influence of magneto-dipole interaction leads to increase of the SAR with respect to the case of assembly of non-interacting nanoparticles, as the SAR of the assembly of non-interacting nanoparticles is very small for nanoparticles with diameters D  ≤ 17 nm.

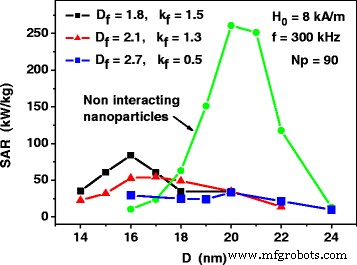
SAR as a function of the average nanoparticle diameter D for dilute assemblies of fractal clusters of nanoparticles with various fractal descriptors. The SAR of the assembly of non-interacting nanoparticles is calculated by means of Eqs. (1) and (2)

The calculations shown in Fig. 4 were carried out assuming the existence of thin non-magnetic shells with thickness t _Sh  = 1 nm at the surface of magnetic nanoparticles. This prevents the nanoparticles of the fractal cluster from direct exchange interaction. Evidently, the increase of the non-magnetic shell thickness reduces the intensity of the magneto- dipole interaction of closest nanoparticles, as the average distance between the magnetic cores on the nanoparticles increases. Figure 5 shows that the increase of the non-magnetic shell thickness is a proper way to raise the SAR of the assembly of fractal clusters of nanoparticles. Namely, for sufficiently large thickness of non-magnetic shells the dependence of the SAR on the particle diameter resembles that for weakly interacting magnetic nanoparticles. This fact may be important for the application of magnetic nanoparticle assemblies in magnetic hyperthermia.

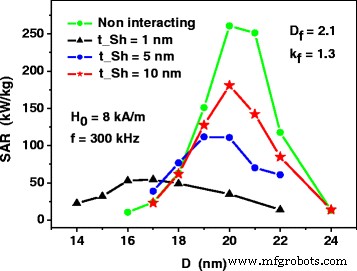
The dependence of the SAR of dilute assembly of fractal clusters on the thickness t _Sh of the non-magnetic shells at the surface of the nanoparticles. The SAR of the assembly of non-interacting nanoparticles is calculated by means of Eqs. (1) and (2)

Conclusions

The main conclusion of this study is that the SAR of a dilute assembly of clusters of magnetic nanoparticles in alternating magnetic field is significantly reduced with increasing of the intensity of magneto-dipole interaction in the clusters. For usual 3D clusters of nanoparticles, the intensity of the magneto-dipole interaction can be characterized by dimensionless packing density, η  = N _p V /V _cl  = (D /D _av ) ³ . The latter determines the average distance between the nanoparticles of the cluster. The calculations show that for the assembly of random 3D clusters, the energy absorption peak, which for iron oxide nanoparticles corresponds to particles with average diameter D  = 20 nm, is reduced about six times when the packing density increases from η  = 0.005 up to η  = 0.32. The dependence of the assembly SAR on the mean nanoparticle diameter is retained with increase of η , but becomes less pronounced.

For dilute assemblies of fractal clusters of magnetic nanoparticles, the SAR values also decrease several times irrespective on the fractal descriptors of the assembly. In addition, the peak values of SAR are shifted systematically to smaller particle diameters, as a rule. It is important to note, however, that the increase of the non-magnetic shell thickness at the nanoparticle surfaces restores the SAR values close to that of the assembly of weakly interacting nanoparticles. This fact can be important for various biomedical applications of magnetic nanoparticle assemblies.

The model considered in this paper takes into account the geometrical structure of nanoparticle assemblies observed experimentally in biological media [4, 8, 9] (in particular in tumors), i.e., the agglomeration of nanoparticles in a sufficiently dense fractal clusters of different sizes, with different numbers of nanoparticles in the clusters. The stochastic LL Eq. (3) accurately describes the real dynamics of the magnetic moments of nanoparticles taking into account both the magneto-dipole interaction between the particles and the effect of thermal fluctuations. The cluster model studied allows obvious generalization that can make it more practical. First, it is necessary to take into account the size distribution of magnetic nanoparticles in the assembly. Second, in some cases exchange interaction may exist between neighboring nanoparticles of the cluster if they are in direct atomic contact.

The theoretical results obtained in this study seem to be in a satisfactory agreement with recent experimental data [35] for iron oxide nanoparticles of optimal diameters. Indeed, according to Ref. [35], the SAR of the iron oxide nanoparticles increases with the average diameter of the nanoparticles and peaks for nanoparticles with mean diameter D  = 20–21 nm. In addition, the SAR decreases [35] with a decrease in the average distance between the nanoparticles due to increasing intensity of the magneto-dipole interaction.

Unfortunately, in some experimental studies [5, 21] carried out to optimize the properties of magnetic nanoparticles for use in magnetic hyperthermia, often do not take into account the theoretical predictions [10, 11] about significant dependence of the assembly SAR on the characteristic size of the magnetic nanoparticles. As shown in this paper, this dependence can be substantial even for rather dense nanoparticle assemblies. From a theoretical point of view, it is obvious [10] that the assembly of iron oxide nanoparticles with very small, D  ≤ 10 nm, or too big, D  ≥ 30 nm diameters can hardly provide a sufficiently high SAR values for typical for magnetic hyperthermia frequencies, f  = 200–600 kHz, and magnetic field amplitudes H ₀  ~ 8 kA/m. The creation of mono-crystalline iron oxide nanoparticles with sharp size distribution near the optimal diameter has to be promising for application in magnetic hyperthermia.

Um novo sensor de espalhamento Raman otimizado para superfície inteligente baseado em nanopartículas de ag capadas com poliacriloil hidrazina responsivas ao pH Em direção a cadeias de átomo único com telúrio esfoliado