Difração de raios X de alta pressão in situ e estudo de espectroscopia Raman de Ti3C2Tx MXene

Resumo

A estabilidade da rede e a resposta de fônon de Ti ₃ C ₂ T _x MXene em alta pressão são importantes para a compreensão completa de suas propriedades mecânicas e térmicas. Aqui, usamos difração de raios-X de alta pressão hidrostática in situ (XRD) e espectroscopia Raman para estudar a deformação da rede e o comportamento do fônon de Ti ₃ C ₂ T _x MXene. Os espectros de XRD indicam que nenhuma transformação de fase ocorre até a pressão de 26,7 GPa. A constante elástica ao longo de a o parâmetro de rede foi calculado em 378 GPa. Nos espectros Raman obtidos em alta pressão, os modos de fônon fora do plano ( A _1g em ~ 210, ~ 504 e ~ 711 cm ⁻¹ ) exibem blueshifts monotônicos com o aumento da pressão. Os parâmetros de Grüneisen desses três modos foram calculados em 1,08, 1,16 e 0,29, respectivamente. Esses resultados enriquecem os dados básicos de propriedade de Ti ₃ C ₂ T _x MXene e beneficiaria uma maior compreensão deste novo material.

Histórico

Após os estudos intensivos de grafeno [1] e dichalcogenetos de metais de transição (TMDs) [2,3,4,5] por uma década, carbonetos metálicos bidimensionais (2D) (MXenes) têm chamado muita atenção recentemente devido ao seu extraordinário propriedades elétricas [6, 7]. O Ti ₃ C ₂ MXene é um material em camadas com estrutura empilhada de Van der Waals, em que cada camada contém dois planos de átomos de carbono ensanduichados entre três planos de átomos de Ti. Na estrutura da banda de energia de Ti ₃ C ₂ MXene, a banda de condução toca a banda de valência no ponto Γ, o que indica que Ti ₃ C ₂ MXene é um material semimetálico [8]. Mais interessante, a estrutura da banda de Ti ₃ C ₂ Mxene pode ser ligeiramente aberto pelos grupos funcionais de superfície (que são anotados como “T” na fórmula) [8], como –F, –O e –OH [9]. Esses grupos funcionais são gerados na solução de corrosão de M _n AlC _{n + 1} fase [9], que então forma um Ti ₃ C ₂ T _x MXene com propriedades elétricas ajustáveis. A condutividade elétrica de Ti ₃ C ₂ T _x MXene foi medido como 4,2 × 10 ⁻⁴ S / m [10], que é superior à maioria dos TMDs. Até o momento, Ti ₃ C ₂ T _x MXenes têm mostrado aplicações potenciais em supercapacitores avançados [11], baterias de lítio [12], blindagem eletromagnética [10], antibacteriano [13] , e emissão de luz [14].

Além da alta condutividade elétrica, a propriedade elástica de Ti ₃ C ₂ T _x MXene também atrai muita atenção. Cálculos teóricos previram que este carboneto ultrafino tem um módulo de Young de até ~ 500 GPa [15,16,17]. Lipatov et al. recentemente usou nanoindentação para determinar que o módulo de Young da monocamada Ti ₃ C ₂ T _x MXene era de 330 Gpa [18]. Esses valores são muito maiores do que os do MoS ₂ [18] e são comparáveis aos de grafeno monocamada [19]. Recentemente, Ghidiu et al. mediu os espectros de difração de raios-X de alta pressão (XRD) de Ti ₃ C ₂ T _x MXene até 3 GPa e não observou nenhuma transformação de fase [20]. No entanto, como a pressão carregada na ref. [20] era muito baixo, a estabilidade de fase e deformação da rede de Ti ₃ C ₂ T _x em alta pressão ainda são desconhecidos.

A espectroscopia Raman atua como uma ferramenta não destrutiva útil para investigar a estrutura cristalina e a vibração de fônons de materiais 2D como o grafeno [21] e TMDs [2]. A composição de Ti ₂ CT _x [22] e estabilidade de fase de Ti ₃ C ₂ T _x Mxene em diferentes condições de recozimento [10] pode ser sondado usando medições Raman confocais. Recentemente, a dispersão de fônons de Ti ₃ C ₂ T _x MXene foi teoricamente calculado por Hu et al. [23, 24], permitindo assim um melhor entendimento dos espectros Raman deste material. No entanto, a espectroscopia Raman de alta pressão de Ti ₃ C ₂ T _x ainda está faltando. Além disso, a resposta de fônon de Ti ₃ C ₂ T _x em função da pressão é desconhecida.

Neste artigo, preparamos Ti ₃ C ₂ T _x flocos finos e mediram seus espectros de XRD e Raman dependentes de pressão de até 26,7 GPa. As constantes elásticas de Ti ₃ C ₂ T _x foram calculados a partir de desvios de pico de difração de XRD pela equação de Murnaghan. Os parâmetros de Grüneisen positivos de fônons fora do plano foram obtidos a partir do deslocamento Raman dependente da pressão e da razão de deformação do parâmetro de rede. Os resultados obtidos beneficiariam o melhor entendimento do comportamento mecânico e fonon-vibracional do Ti ₃ C ₂ T _x MXene.

Resultados e discussões

Antes de realizar medições de alta pressão, primeiro investigamos as propriedades básicas do material do Ti esfoliado ₃ C ₂ T _x Flocos Mxene. Uma imagem ótica do esfoliado Ti ₃ C ₂ T _x flocos depositados em Si / SiO ₂ (300 nm) substrato é mostrado na Fig. 1a. O contraste verde claro pode ser observado para os flocos esfoliados. Conforme relatado por Miranda et al., O contraste óptico de Ti ₃ C ₂ T _x flocos depende fortemente da espessura do floco, onde flocos mais grossos sempre mostram maior contraste, enquanto flocos finos exibem baixo contraste [25]. O contraste verde claro da maioria dos flocos na Fig. 1b indica sua espessura fina. Uma imagem topográfica de microscópio de força atômica (AFM) de Ti esfoliado ₃ C ₂ T _x flocos é mostrado na Fig. 1b. Os flocos na área de mapeamento mostram superfícies com alta rugosidade, o que é típico para Ti ₃ C ₂ T _x flocos [26]. A espessura de um floco fino típico pode ser determinada a partir de seu perfil de linha (inserção da Fig. 1b) através da posição marcada na Fig. 1b como sendo 170 nm. Uma imagem de microscópio eletrônico de varredura (SEM) de um floco esfoliado é mostrada na Fig. 1c. A estrutura laminada de Ti ₃ C ₂ T _x pode ser visto claramente, indicando a preparação bem-sucedida do Ti ₃ C ₂ T _x amostras em camadas [10].

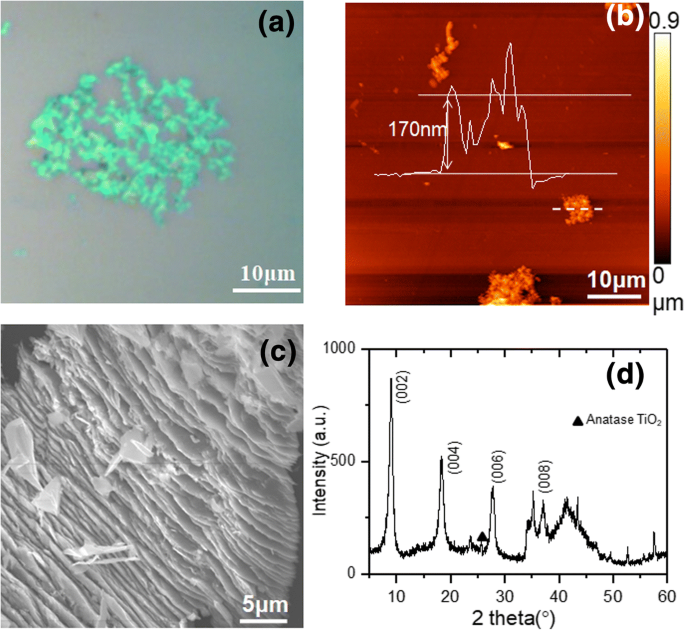
a Imagem ótica de Ti ₃ esfoliado ultrassonicamente C ₂ T _x flocos; b Imagem topográfica AFM de Ti ₃ esfoliado por ultrassom C ₂ T _x flocos, e um perfil de linha através da linha tracejada marcada é mostrado como uma inserção, indicando o Ti ₃ C ₂ T _x espessura do floco de 170 nm; c Imagem SEM de Ti ₃ esfoliado ultrassonicamente C ₂ T _x flocos; d Espectros de XRD de Ti ₃ C ₂ T _x pó cru

Medimos ainda os espectros de XRD de Ti bruto ₃ C ₂ T _x pó, como mostrado na Fig. 1d. Este padrão de XRD é uma analogia com relatórios anteriores [10]; assim, os picos proeminentes em 8,95 °, 18,28 ° e 27,7 ° podem ser atribuídos às difrações dos planos (002), (004) e (006). Em comparação com os picos proeminentes, a intensidade dos picos de difração de fases menores (anatase TiO ₂ (101) a 25,3 °, Cartão JCPDS No. 71-1116) é relativamente fraco, indicando a alta pureza de Ti ₃ C ₂ T _x fase no pó obtido. O pico (002) emerge em um ângulo ligeiramente inferior ao relatado por Han et al. (9,21 °) [10]. O c calculado o parâmetro de rede, 19,66 Å, é maior do que o valor relatado (19,2 Å) [10]. Deve-se notar que, uma vez que o espaço intercamada pode ser ajustado por diferentes densidades de grupos químicos e íons, como –F, –OH e Li ⁺ , o c o parâmetro de rede varia substancialmente de 19,2 Å a 58,8 Å em diferentes estudos [10, 20, 26, 27]. O c parâmetro de rede para nossa amostra está muito próximo do valor baixo que foi medido para Ti ₃ C ₂ T _x pó simplesmente usando HF como condicionador [10].

Os espectros de XRD de Ti ₃ C ₂ T _x flocos medidos em diferentes pressões até 26,7 GPa são mostrados na Fig. 2a. Pode-se ver que os espectros medidos em diferentes pressões são semelhantes entre si, enquanto nenhum novo pico de difração pode ser encontrado. Esse achado indica que nenhuma transformação de fase ocorre com a pressão de até 26,7 GPa. Na Fig. 2a, todos os picos de difração mudam para grandes ângulos com o aumento da pressão, indicando o encolhimento do Ti ₃ C ₂ T _x treliça. Tal compressibilidade pseudo-negativa também foi observada para Ti ₃ C ₂ T _x [20] e outros materiais de baixa dimensão com uma estrutura em camadas, como grafite [28], óxido de grafeno [29, 30], MoS ₂ [31], argila [32] e titanatos [33]. O pico (002) muda de 2,883 ° para 3,162 ° conforme a pressão aumentou de 1,8 GPa para 26,7 GPa. A taxa de deformação do parâmetro de rede c , c / c ₀ , como uma função da pressão, pode ser calculado a partir do deslocamento do pico (002). Além disso, a taxa de deformação de a , a / a ₀ , pode ser calculado a partir do deslocamento do pico (110). Conforme mostrado na Fig. 2b, os parâmetros de rede c e a são deformados em 9,1% e 2,4%, respectivamente, a uma pressão de 26,7 GPa. Na região de baixa pressão em ~ 3 GPa, a razão de compressão do parâmetro de rede c é de 3%. Na medição anterior de XRD de alta pressão de Ti ₃ C ₂ T _x flocos, um c ligeiramente maior taxa de compressão de 4% para Ti seco ₃ C ₂ T _x flocos foi relatado por Ghidiu et al. [11] (Fig. 2b). Esta diferença pode ser induzida por um parâmetro de rede maior c (25,1 Å) da amostra usada por Ghidiu et al. [11] com respeito ao nosso (19,66 Å).

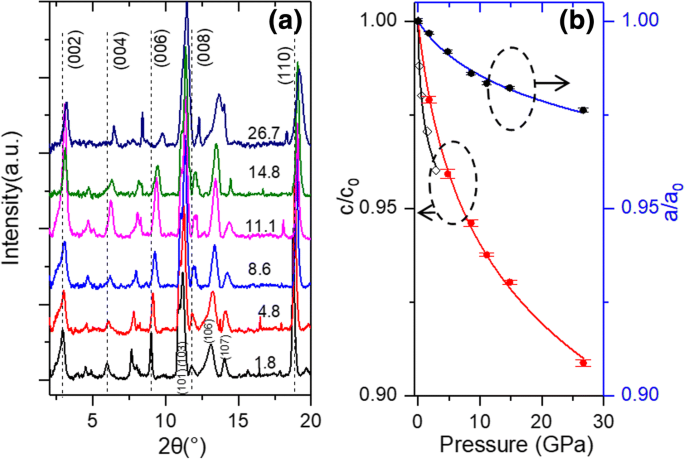
a Espectros de XRD de Ti ₃ C ₂ T _x em diferentes pressões carregadas. Observe que a unidade é GPa para a pressão anotada em cada espectro. Os picos são atribuídos de acordo com a ref. [26]; b experimental (pontos) e razão de compressão calculada (linha sólida) ao longo de c e a instruções. As linhas sólidas são os resultados ajustados usando a equação \ (r (P) / {r} _0 ={\ left [\ left ({\ delta} _0 / {\ delta} ^ {\ prime} \ right) P + 1 \ right]} ^ {\ delta ^ {\ prime}} \)

Para obter as constantes elásticas, o c e a as taxas de compressão na Fig. 2b são posteriormente ajustadas usando a equação de Murnaghan [34].
$$ r (P) / {r} _0 ={\ left [\ left ({\ beta} ^ {\ prime} / {\ beta} _0 \ right) P + 1 \ right]} ^ {- 1 / { \ beta} ^ {\ prime}} $$ (1)
onde r representa as constantes de rede ao longo de c e a eixos, \ ({\ beta} _0 ^ {- 1} =- {\ left (\ frac {dlnr} {lnP} \ right)} _ {P =0} \) é a compressibilidade linear, e β ^′ é a derivada de pressão de β .

O equipado r / r ₀ curvas de a e c são plotados como linhas sólidas na Fig. 2b. Pode-se observar que os resultados experimentais se enquadram muito bem na expectativa da equação. O melhor ajuste gera β ₀ e β ^′ para c como 67,7 GPa e 25,5, respectivamente. Enquanto para o parâmetro de rede a , β ₀ e β ^′ são calculados em 387,4 GPa e 72,1, respectivamente (Tabela 1). Para materiais 2D ultrafinos, como o grafeno, o módulo de Young (1TPa) é muito próximo do β ₀ de grafite espesso [19, 28]. Portanto, β ₀ pode ser usado como uma substituição para avaliar a constante elástica de Ti ₃ C ₂ T _x . Módulo de Young de Ti ₃ C ₂ T _x foi medido recentemente por Lipatov et al. para ser 330 GPa [18], o que é consistente com o β ₀ em nosso estudo. Nossos valores medidos também são comparáveis às constantes elásticas de Ti ₃ C ₂ que foram calculados em outros estudos [15, 17] (Tabela 1). O β ₀ em c eixo é maior do que o da grafite ( β ₀ = 35,7 GPa), enquanto o β ₀ em a eixo é menor do que o da grafite ( β ₀ = 1250 GPa) [28]. O β ₀ de Ti ₃ C ₂ T _x é maior do que o módulo em massa de MoS ₂ (270 Pa) [35] e também é comparável ao do óxido de grafeno (210 GPa) [36], indicando uma alta constante elástica de Ti ₃ C ₂ T _x Mxene entre materiais 2D.

Espectros Raman de alta pressão de Ti ₃ C ₂ T _x as amostras foram medidas em diferentes pressões de compressão de até 25,5 GPa, conforme mostrado na Fig. 3a. Os espectros Raman obtidos em diferentes pressões descompressivas são mostrados na Fig. 3b. Em baixas pressões de compressão, Ti ₃ C ₂ T _x Mxene exibe três bandas Raman principais em ~ 210, ~ 500 e 700 cm ⁻¹ . Deve-se notar que os espectros Raman de Ti ₃ C ₂ T _x MXene varia significativamente em diferentes tipos de literatura. Hu et al. [23] relatou fortes picos Raman em ~ 200 cm ⁻¹ e 720 cm ⁻¹ , enquanto outras bandas a 400 cm ⁻¹ eram bastante amplos. No entanto, Han et al. [10] e Zhu et al. [37] observou um pico agudo em ~ 200 cm ⁻¹ , mas outras bandas eram todas amplas. Xue et al. [14] observou apenas picos amplos de 100 a 700 cm ⁻¹ . Os espectros Raman na Fig. 3 são diferentes daqueles na ref. [10, 14, 23, 37]. Esta diferença pode ser induzida por diferentes tipos e concentrações de grupos químicos no Ti ₃ C ₂ T _x MXene. Uma interpretação posterior dessas diferentes bandas Raman precisa lembrar a dispersão de fônons de Ti ₃ C ₂ T _x que foi calculado teoricamente por Hu et al. [23, 24]. O grupo espacial de Ti ₃ C ₂ T _x era P6 ₃ / mmc [23]. O número de átomos ( N ) em uma célula primitiva de Ti ₃ C ₂ T _x foi calculado em 7, 7 e 9 para T =−O, −F e −OH, respectivamente, dado x =2. Em Γ ponto da primeira zona de Brillouin, prevê-se que os seguintes fônons ópticos existam para diferentes Ti ₃ C ₂ T _x MXenes: Γ _óptico (Ti ₃ C ₂ O ₂ ) =6 E _g + 3 A _1g , Γ _óptico (Ti ₃ C ₂ F ₂ , Ti ₃ C ₂ (OH) ₂ ) =8 E _g + 4 A _1g [23]. As vibrações do átomo de diferentes modos ativos Raman de Ti ₃ C ₂ F ₂ e Ti ₃ C ₂ (OH) ₂ são ilustrados esquematicamente na Tabela 2. Suas frequências foram calculadas teoricamente por Hu et al. [23] e estão listados na Tabela 2. Para Ti ₃ C ₂ (OH) ₂ , existem quatro modos fora do plano ( A _1g :218, 514, 684 e 3734 cm ⁻¹ ) e quatro modos no avião ( E _g :138, 278, 437 e 622 cm ⁻¹ ) Para Ti ₃ C ₂ F ₂ , existem três A _1g modos (190, 465 e 694 cm ^{- 1} ) e três E _g modos (128, 231 e 612 cm ^{- 1} ) [23].

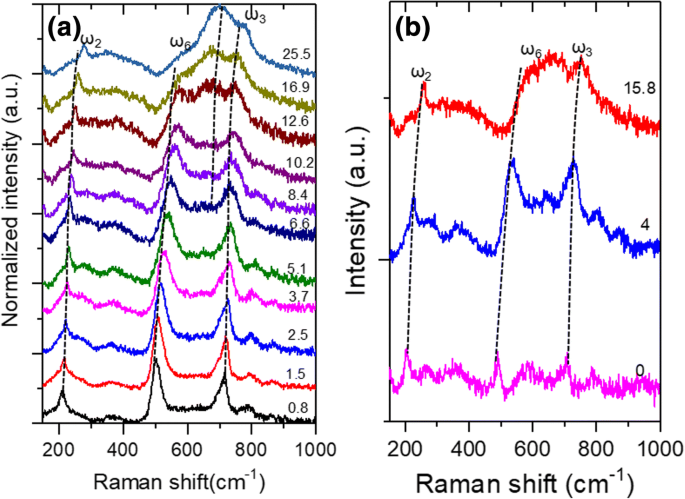
a Espectros Raman de Ti ₃ C ₂ T _x flocos em diferentes pressões de compressão; b Espectros Raman obtidos em diferentes pressões de descompressão. Observe que a unidade de pressão em a e b é GPa

No entanto, podem ser vistas as frequências de fônons calculadas do Ti puro ₃ C ₂ F ₂ ou Ti ₃ C ₂ (OH) ₂ não pode se ajustar aos espectros Raman experimentais de Ti ₃ C ₂ T _x na Fig. 3. Porque a superfície de Ti ₃ C ₂ T _x é geralmente anexado por um tipo diferente de grupos químicos, uma interpretação completa dos espectros Raman experimental na Fig. 3 precisa considerar os modos de vibração hibridizados de −F e −OH [23]. Em uma pesquisa anterior [23], as bandas Raman em ~ 200, ~ 500 e ~ 700 cm ⁻¹ foram atribuídos a ω ₂ , ω ₆ , e ω ₃ , respectivamente. Seguindo esta instrução, as bandas Raman proeminentes em 205,6, 490,2 e 702,5 cm ⁻¹ da Fig. 3a, b pode ser atribuído a ω ₂ , ω ₆ , e ω ₃ modos, respectivamente. Curiosamente, esses modos são todos modos fora do plano. Outros modos Raman são difíceis de serem isolados de seus modos vizinhos devido às suas baixas intensidades. Para obter dados robustos eliminando as incertezas, apenas esses três modos são considerados nos cálculos e análises a seguir.

Nas Fig. 3a, b, também pode ser visto que as intensidades relativas desses modos no plano aumentam com o aumento das pressões compressivas (Fig. 3a). Quando a pressão de compressão é ≥ 12,6 GPa, um novo pico em ~ 600 cm ⁻¹ (ω ₄ ) emerge e se torna o pico proeminente. No processo de descompressão, as intensidades deste ω ₄ modo diminuir significativamente. Os espectros Raman obtidos a 0 GPa de pressão de descompressão contêm quase todos os modos de fônon no plano e fora do plano. Tal emergência de modos no plano em alta pressão compressiva pode estar relacionada com fratura em flocos ou polarização induzida por rotação de orientação. A pesquisa sobre esse efeito ainda está em andamento e será relatada no futuro.

Com o aumento da pressão de 0,8 GPa para 25,6 GPa, ω ₂ , ω ₆ , e ω ₃ todos mostram blueshifts monotônicos crescentes (Fig. 4a-d), que são semelhantes aos blueshifts dependentes de pressão do grafite [28] e MoS ₂ [31]. A 25,6 GPa, os blueshifts desses três modos são 66,7, 85,1 e 60 cm ⁻¹ , respectivamente. Esses blueshifts dependentes de pressão são muito maiores do que os do MoS ₂ [31]. Para quantificar o deslocamento Raman vs pressão, os gráficos de deslocamento Raman na Fig. 4a, b, d foram ajustados usando a seguinte equação [28]:
$$ \ omega (P) / {\ omega} _0 ={\ left [\ left ({\ delta} _0 / {\ delta} ^ {\ prime} \ right) P + 1 \ right]} ^ {\ delta ^ {\ prime}} $$ (2)

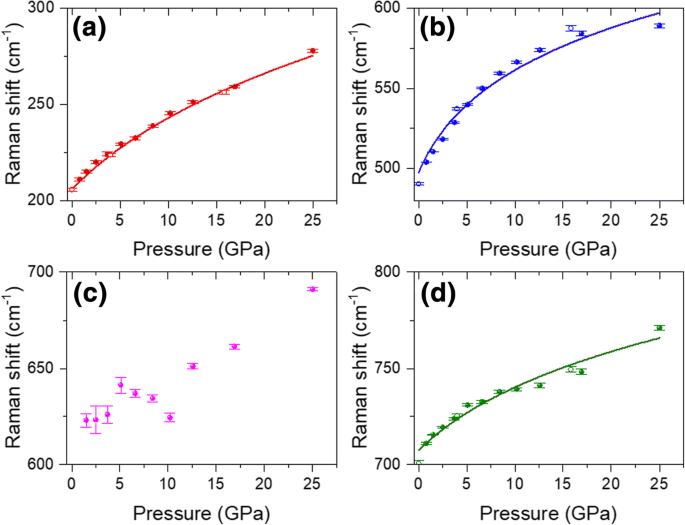
Mudanças Raman de diferentes modos de fônon em função de diferentes pressões compressivas (esfera sólida) e descompressivas (círculos abertos): a 210 cm ⁻¹ , b 504 cm ⁻¹ , c 620 cm ⁻¹ , e d 711 cm ⁻¹ . As linhas sólidas são os resultados do ajuste usando a equação \ (\ omega (P) / {\ omega} _0 ={\ left [\ left ({\ delta} _0 / {\ delta} ^ {\ prime} \ right) P + 1 \ right]} ^ {\ delta ^ {\ prime}} \)

onde δ ₀ e δ ^′ são os derivados logarítmicos da pressão ( dlnω / dP ) _{P =0} e a derivada de pressão de dlnω / dP , respectivamente. Os resultados ajustados são plotados como linhas sólidas na Fig. 4a, b, d. Devido às altas incertezas na região de baixa pressão, o modo Raman em 620 cm ⁻¹ não foi instalado. Pode-se observar na Fig. 4a, b, d que as curvas ajustadas são consistentes com os resultados experimentais, indicando a alta precisão do processo de ajuste. Os parâmetros obtidos de δ ₀ e δ ^′ estão listados na Tabela 3.

Para materiais anisotrópicos 2D com espessura atômica, como MXene e grafeno, dois componentes independentes dos tensores de Grüneisen são geralmente associados às deformações que são paralelas e perpendiculares ao c eixo. Para simplificar, adotamos a relação de escala proposta por Zallen et al. [38], que foi usado para ajustar o deslocamento Raman dependente da pressão da grafite por Hanfland et al. [28]
$$ \ omega (P) / {\ omega} _0 ={\ left [r (P) / {r} _0 \ right]} ^ {3 \ gamma} $$ (3)
onde r refere-se às constantes de rede no plano e fora do plano para os modos intralamada e intercamada, respectivamente. γ equivale ao parâmetro Grüneisen que foi definido em outros estudos [39, 40].

Como apenas os modos fora do plano são observados no processo de compressão, c O parâmetro de rede em função da pressão hidrostática é adequado para o cálculo. Adotamos os dados de distância espacial do plano (002) de 0 a 26,7 GPa na Fig. 2b para o cálculo do parâmetro de Grüneisen γ . A média de \ (\ overline {\ upgamma} \) até 26,7 GPa para ω ₂ , ω ₆ , e ω ₃ foram calculados em 1,08, 1,16 e 0,29, respectivamente (Tabela 2). Semelhante ao grafite, o menor \ (\ overline {\ upgamma} \) de ω ₃ em comparação com os outros dois modos, indica que uma mudança menor nas constantes de força está envolvida no movimento da camada rígida [28]. Até onde sabemos, os parâmetros Grüneisen de Ti ₃ C ₂ T _x não foram relatados ainda. No entanto, ainda podemos comparar nossos dados com outros materiais 2D. Zha et al. Parâmetros Grüneisen relatados como 4–5 para modos de fônon acústico de Ti ₂ CO ₂ [41]. Como os parâmetros de Grüneisen dos modos ópticos de alta frequência são geralmente uma ou duas ordens inferiores aos dos modos de baixa frequência [28], os parâmetros de Grüneisen para fônons ópticos de Ti ₂ CO ₂ pode ser estimado em 0,05–0,5, que são semelhantes aos nossos valores para Ti ₃ C ₂ T _x . Recentemente, Peng et al. [42] relatou os parâmetros de Grüneisen à temperatura ambiente como 1,22, 1,20 e 1,15 para MoS ₂ , MoSe ₂ e WS ₂ , respectivamente, que são maiores do que nossos resultados. Nossos resultados também são menores do que os do grafeno (1,99 para E _2g modo) [40] e grafite (1,06 para E _2g modo) [28]. Esta descoberta indica que Ti ₃ C ₂ T _x MXene tem a anarmonicidade de ligação mais fraca entre esses materiais 2D ultrafinos [42].

Conclusões

Em conclusão, medimos a deformação da rede e a resposta do fônon de Ti ₃ C ₂ T _x flocos finos em diferentes pressões hidrostáticas de até 26,7 GPa. Nenhuma transformação de fase foi observada abaixo de uma pressão de 26,7 GPa. Todos os modos de fônon mostram uma mudança de frequência positiva com o aumento das pressões. Os parâmetros Grüneisen positivos de três fônons fora do plano são calculados em 1,08, 1,16 e 0,29. Nossos resultados aumentam a compreensão das propriedades mecânicas e térmicas do Ti ₃ C ₂ T _x em altas pressões.

Métodos

Ti ₃ C ₂ T _x o pó foi preparado por um método relatado pela referência [43]. Resumidamente, Ti ₃ AlC ₂ pó (Forsman, 10 g) foi atacado por solução de HF (160 ml) à temperatura ambiente durante 5 h. O Ti obtido ₃ C ₂ T _x o pó foi disperso em água DI e esfoliado por ultrassom a uma potência de 700 W. A solução resultante foi separada após ser armazenada por 24 h. A solução da camada superior obtida foi usada para análises adicionais de Raman, microscópio de força atômica (AFM) e microscópio eletrônico de varredura (MEV). Os espectros de difração de raios-X (XRD) à pressão ambiente foram medidos usando um difratômetro de raios-X (Rigaku, MiniFlex600). Imagens SEM foram obtidas usando um microscópio eletrônico de varredura (Hitachi, Su1510). As medições de XRD de alta pressão in situ foram realizadas no Shanghai Synchrotron Radiation Facility por uma gaxeta de célula de bigorna de diamante de alta pressão (DAC) em temperatura ambiente. Para produzir um ambiente hidrostático ao redor da amostra, usamos metanol / etanol / água (16:3:1) como meio de transmissão de pressão. A pressão foi determinada pelo desvio espectral dependente da pressão da linha R1 de fluorescência rubi nítida. A amostra foi colocada em um orifício de junta de aço inoxidável (100 μm de diâmetro) com um culet de diamante (400 μm de diâmetro). As medições de espalhamento Raman de alta pressão foram realizadas usando um espectrômetro Renishaw inVia Raman com um comprimento de onda de excitação de 532 nm. As medidas topográficas foram realizadas em um instrumento AFM (Bruker, Innova).

O ajuste de posições de pico de difração e mudanças de pico Raman foi conduzido no pacote OriginPro. Uma função definida pelo usuário, y =(A1 × x + 1) ^A2 , foi usado definindo A1 e A2 como os parâmetros de ajuste. O encaixe adequado pode ser obtido facilmente por um método simplex.

Abreviações

2D:: Bidimensional
AFM:: Microscópio de força atômica
DAC:: Bigorna de diamante
SEM:: Microscópio eletrônico de varredura
TMDs:: Dichalcogenetos de metais de transição
XRD:: Difração de raios X

Preparação e propriedades eletroquímicas de ânodos Fe2O3 / C em forma de romã para baterias de íon-lítio Projeto racional de Ni (OH) 2 Arquitetura porosa oca para sensor de glicose livre de enzima de alta sensibilidade

Nanomateriais

Materiais Poliméricos

biológico

Corante

Especiarias