Um estudo de nanofibras de carbono e carbono ativo como supercapacitor simétrico em eletrólito aquoso:um estudo comparativo

Resumo

Supercapacitores simétricos são fabricados por nanofibras de carbono (CNF) e carvão ativado (AC) usando proporções semelhantes de 7% em peso de um aglutinante de polímero de fluoreto de polivinilideno (PVDF) em um eletrólito aquoso. Neste estudo, uma comparação de textura porosa e desempenho eletroquímico entre CNFs e supercapacitores baseados em AC foi realizada. Os eletrodos foram montados na célula sem um coletor de corrente. Os eletrodos preparados de CNFs e AC apresentam área de superfície Brunauer-Emmett-Teller (BET) de 83 e 1042 m ² / g, respectivamente. A estrutura de poros dominante para CNFs é mesoporosa, enquanto para AC é micropore. Os resultados mostraram que a CA fornece maior retenção de capacitância específica até uma taxa de varredura muito rápida de 500 mV / s. O carbono AC tinha uma capacitância específica de 334 F / g e os CNFs tinham 52 F / g a uma taxa de varredura de 5 mV / s em solução aquosa. Além disso, os resultados indicam a condutividade superior dos CNFs em contraste com as contrapartes AC. A resistência série equivalente medida (ESR) apresentou um valor muito pequeno para CNFs (0,28 Ω) em comparação com AC que tem uma resistência ESR de (3,72 Ω). Além disso, o CNF entregou uma potência específica mais alta (1860 W / kg) do que a CA (450 W / kg). Por outro lado, a CA deu energia específica mais alta (18,1 Wh / kg) do que a dos CNFs (2 Wh / kg). Isso indica que a CA é boa para aplicações de energia. Considerando que o CNF é bom para aplicação de energia. Na verdade, a área de superfície mais alta levará a uma capacitância específica mais alta e, portanto, a uma densidade de energia mais alta para CA. Para CNF, menor ESR é responsável por ter maior densidade de potência.

Tanto o supercapacitor CNF quanto o AC exibem uma excelente estabilidade de carga-descarga de até 2.500 ciclos.

Histórico

Supercapacitores ou capacitores eletroquímicos têm atraído muito interesse devido à sua alta densidade de potência e longos ciclos de recursos. Eles encontraram aplicações potenciais em veículos elétricos, dispositivos portáteis e ferramentas elétricas [1]. Os veículos elétricos precisam de alta potência com alta taxa de drenagem de corrente, enquanto os sistemas de backup de memória requerem alta densidade de energia com baixa taxa de drenagem de corrente. Conseqüentemente, o material deve ser escolhido de acordo com as aplicações desejadas [2]. Os principais componentes de um supercapacitor são os eletrodos e o eletrólito. Uma vez que o armazenamento de carga ocorre na interface eletrodo / eletrólito, a área de superfície do eletrodo e o eletrólito usado influenciarão muito o desempenho do dispositivo. As propriedades do eletrodo de natureza material, espessura do eletrodo, área de superfície, distribuição de tamanho de poro e grupos de superfície influenciam fortemente o desempenho do supercapacitor [3]. Materiais de carbono são amplamente utilizados como eletrodos devido ao seu baixo custo, diversidade de morfologias disponíveis e estabilidade química e térmica [4,5,6,7]. A morfologia tubular em nanoescala CNF pode oferecer uma combinação única de baixa resistividade elétrica e alta porosidade em uma estrutura facilmente acessível [8]. Um material AC é muito atraente para supercapacitores devido à alta porosidade, baixo custo, abundância, alta estabilidade e ciclo de carga-descarga [9]. A fabricação de eletrodos (AC ou CNFs) para supercapacitores requer a adição de aglutinante - por exemplo, poli (tetrafluoroetileno) (PTFE), cloreto de polivinilideno (PVDC) e fluoreto de polivinilideno (PVDF) - em proporções que geralmente variam de 5 a 10 em peso . % para manter a integridade dos eletrodos [10, 11]. No entanto, o ligante bloqueia a parte da porosidade do carbono e, adicionalmente, causa um aumento na resistividade elétrica [11,12,13].

A capacitância do supercapacitor está altamente ligada ao material do eletrodo e ao eletrólito. A compatibilidade do eletrólito com o material do eletrodo também desempenha um papel crucial no desenvolvimento do supercapacitor porque a dupla camada elétrica é construída na interface eletrodo / eletrólito. A voltagem de um supercapacitor depende da janela do potencial de estabilidade do eletrólito. Os eletrólitos aquosos geralmente fornecem potencial até 1,0 V e eletrólito orgânico até 2,7 V [14]. Eletrólitos aquosos são ecologicamente corretos, enquanto eletrólitos orgânicos não são bons para o meio ambiente. Eletrólitos aquosos são compostos principalmente de pequenos ânions e cátions simples hidratados (nível de angstrom). Esses íons podem penetrar facilmente nos microporos, mesoporos e macroporos do material sob o campo elétrico aplicado. A dupla camada elétrica (EDL) construída na região da interface eletrodo / eletrólito pode ser tratada como um capacitor com um capacitor elétrico de camada dupla (EDLC), que pode ser expresso como C = ϵA / d . Onde ϵ é a constante dielétrica do eletrólito, A é a área de superfície acessível aos íons, e d é a distância dos íons à superfície do poro do eletrodo de carbono na ordem de um angstrom. De acordo com a equação acima, duas abordagens podem ser tomadas para aumentar o armazenamento de carga do EDLC de forma eficaz:aumentando o SSA e reduzindo a distância entre os íons e a superfície do carbono pelo desenvolvimento [15].

Neste trabalho, o objetivo é fornecer uma análise comparativa do supercapacitor simétrico baseado em AC e CNFs usando uma quantidade semelhante de ligante PVDF 7% em peso para ambos os materiais.

Métodos / Experimental

Preparação de eletrodos AC e CNF

O supercapacitor simétrico baseado em AC e CNFs foi preparado para comparação. A referência AC Carbopal CCP80 da Donau Carbon é fornecida pela QuimicsDalmau. Os CNFs têm uma estrutura de copo empilhado helicoidalmente grafítico, há uma presença de Ni (6%), o diâmetro é 20–80 nm, comprimento (MEB)> 30um e resistividade elétrica de 10 ⁻² Ω cm.

PVDF foi usado como um aglutinante. A fim de comparar a preparação do eletrodo para a análise do supercapacitor para ambos os materiais (AC, CNFs) foi obtida de forma semelhante, seguindo as etapas abaixo.

Etapa 1:Moagem de (AC ou CNFs) em um moinho de bolas planetário de zircônia (Pulverisette 7 de Fritch) empregando uma frequência de 500 rpm por 30 min. Etapa 2:Mistura de AC ou CNFs 93% em peso com 7% em peso de polímero PVDF usando 15 ml de acetona em um almofariz de ágata. Etapa 3:A pasta foi então misturada usando um agitador mecânico por 60 min seguido por um ultrassônico por 30 min. Etapa 4:A pasta da mistura foi seca em um forno por 60 min a 70 ° C. Etapa 5:Na última etapa, a lama desidratada foi utilizada para preparar os eletrodos, de certa forma, utilizando-se uma prensa hidráulica com conjunto de matrizes (10 mm) com força de 10 tons. A massa calculada dos discos de eletrodo preparados com base em CNFs e AC foram 0,018 e 0,02 g, respectivamente.

Caracterização da superfície

A textura porosa e área de superfície específica e distribuição de tamanho de poro dos eletrodos CNF e AC foram obtidas por adsorção física de gasesN ₂ a 77 K usando Micromeritics TriStar 3000 V6.04 A. Todas as amostras foram liberadas de gás a 100 ° C por 4 h antes das medições de adsorção. A área de superfície específica ( S _APOSTA , m ² / g) foi determinada pelo método multiponto Brunauer-Emmett-Teller (BET) na região da isoterma, que é limitada pela faixa de pressão relativa P / P ₀ =0,02–0,2. O volume total dos poros ( V _total , cm ³ / g) foi calculado pelo número de nitrogênio adsorvido em P / P ₀ ≈ 0,9932. O volume dos microporos e os valores das áreas superficiais dos micro ( S _micro , m ² / g) foram investigados usando o método t-plot (Harkins e Jura); a distribuição do tamanho dos poros para a amostra CNF é calculada a partir das isotermas de adsorção pelo método Barrett-Joyner-Halenda (BJH); e o método MP é usado para calcular a distribuição do tamanho dos poros para AC.

Caracterização morfológica

As amostras de AC e CNF foram examinadas em microscopia eletrônica de varredura (MEV). As análises de TEM foram realizadas em um sistema Philips Tecnai G2 F20 operado a 300 kV. As amostras foram suspensas em etanol e dispersas por ultrassom por 15 min. Uma gota da suspensão foi depositada sobre uma grade de cobre revestida com carbono.

Caracterização eletroquímica

A comparação do desempenho eletroquímico de AC e CNFs como capacitores simétricos foi estudada em duas células Swagelok de eletrodo e usando um potenciostato Gamry 600 usando solução 6-M de KOH como eletrólito. A capacitância específica dos materiais do eletrodo foi investigada por voltametria cíclica (CV), carga / descarga galvanostática (GCD) e espectroscopia de impedância eletroquímica (EIS).

Resultados e discussão

Caracterização morfológica

A morfologia da superfície dos eletrodos preparados foi investigada por SEM Fig. 1 e TEM Fig. 1 (detalhe). Pode ser visto claramente que o aglutinante de PVDF liga eficazmente os CNFs Fig. 1a e AC Fig. 1b. As diferentes estruturas para ambos os eletrodos de CNFs e AC são visíveis. A estrutura típica do CNF, a forma cilíndrica e a inserção da estrutura dos cristais na Fig. 1a. A imagem TEM de AC demonstra esferas interconectadas com tamanho homogêneo e inserção de superfície mais lisa Fig. 1b.

Imagens SEM e imagens TEM (inserção) para a CNFs e b AC

Textura de poros de CNFs e AC

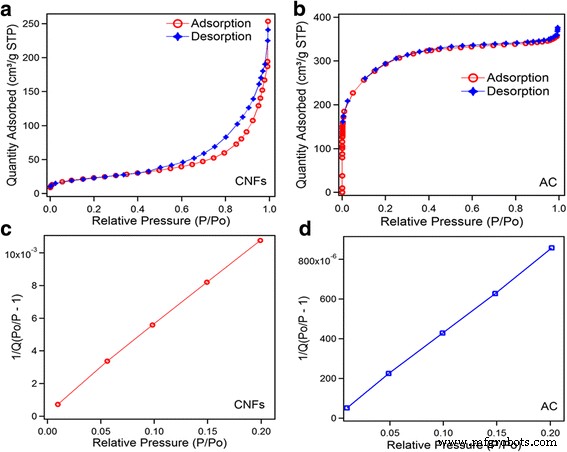
O N ₂ A isoterma de adsorção / dessorção de CNFs e AC é mostrada na Fig. 2. O volume de poro e as distribuições de tamanho de poro foram calculadas pelo método BJH, método t-plot e método MP. Apenas a análise do método MP pode revelar a diferença fina da distribuição do tamanho do microporo da amostra [16]. A distribuição do tamanho dos poros dos materiais é classificada em três grupos:microporos (<2 nm), mesoporos (2-50 nm) e macroporos (> 50 nm) [17]. A isoterma dos CNFs apresenta um pequeno loop de histerese da faixa de pressão superior à média, o que indica que os CNFs contêm estrutura mesoporosa. Devido a isso, apenas o método BJH é usado para detecção de tamanho de poro, uma vez que o método MP não pode detectar meso e macroporosidade. De acordo com a classificação IUPAC, a isoterma dos CNFs pode ser classificada como isoterma do tipo II. A distribuição dos poros dos CNFs é a seguinte:59% mesoporos (2–50 nm), 17,9% microporos (0,5–2 nm) e 23% macroporos (> 50 nm). Os detalhes são apresentados na Tabela 1.

Isotermas de adsorção / dessorção de nitrogênio, a CNFs e b AC BET área de superfície c CNFS e d AC

A isoterma de adsorção / dessorção AC apresenta que a maior parte da quantidade de adsorção ocorre a uma pressão relativa muito baixa ( P / P ₀ ≤ 0,02) e um platô de pressão relativa baixa a alta (0,6–0,8). O volume total do poro é 0,582 cm ³ / g à pressão relativa ( P / P ₀ =0,9932). A Figura 2b apresenta que a curvatura da isoterma de 0 a 0,4 pressão relativa apresenta volume de poro para poros menores que 50 nm (micro + meso), e este volume de poro é igual a 0,534 cm ³ / g que é a indicação de estrutura altamente microporosa. O sistema de isoterma de amostra AC é classificado como isoterma tipo I. A distribuição dos poros da CA é a seguinte:supermicroporos (0,5–2 nm) ocuparam 33%, ultramicro (0,2–0,5 nm) ocuparam 55% e mesoporos ocuparam 12%. O método MP foi usado para detecção de tamanho de poro AC porque o método BJH não pode detectar microporosidade AC. Os detalhes são apresentados na Tabela 1.

A área de superfície específica (BET) foi determinada pelo método de múltiplos pontos Brunauer-Emmett-Teller (BET) na região da isoterma, que é limitada pela faixa de pressão relativa P / P ₀ =0,02–0,2 como visto na Fig. 2c, d. O volume total dos poros (V _total , cm ² / g) foi calculado pelo número de nitrogênio adsorvido em P / P ₀ ≈ 0,9932. O volume de adsorção mostra que as áreas de superfície BET para CNFs e AC são 83 e 1042 m ² / g, respectivamente.

As análises de distribuição de tamanho de poro são apresentadas na Fig. 3a, b obtidas através do método MP para AC e usando o método Barrett-Joiner-Halenda (BJH) para CNFs. Os CNFs contêm dois tipos de poros dominantes centrados nas faixas de 3,36 e 7,1 nm, enquanto o AC é composto principalmente de poros de 0,47 nm. Os micrósporos são benéficos para o acúmulo de carga em eletrólitos aquosos [18, 19]. Pode-se ver que para CNFs, a maioria dos poros dominantes são mesoporos, enquanto para AC ultra-micro poros.

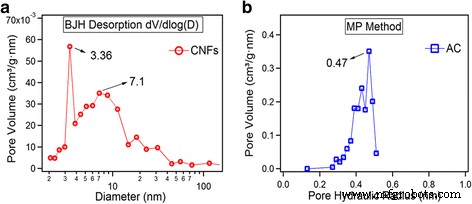
Distribuição do tamanho dos poros. a CNFs pelo método BJH. b Método AC por MP

Comportamento eletroquímico de CNFs e CA

As principais abordagens aceitas para avaliar a capacitância do supercapacitor são voltametria cíclica, carga / descarga galvanostática e espectroscopia de impedância. O princípio de funcionamento de cada técnica varia de um para outro. O comportamento eletroquímico de AC e CNFs foi caracterizado pela primeira vez por voltametria cíclica na faixa de 0 a 1 V. CV é o método mais conveniente para caracterizar o comportamento capacitivo de materiais de eletrodo. A capacitância específica por unidade de massa para um eletrodo foi calculada usando as Eqs. (1, 2).
$$ {C} _ {\ mathrm {s}} =4 \ vezes C / m $$ (1) $$ C =\ frac {q _ {\ mathrm {a}} + \ left | {q} _ {\ mathrm {c}} \ right |} {\ Delta V} $$ (2)
Onde C _s é a capacitância específica em F / g, C é a capacitância medida para a célula de dois eletrodos pela Eq. 2 e m é a massa total do material ativo em ambos os eletrodos [20].

A Figura 4a, b mostra os CVs de CNFs e AC, respectivamente, de taxas de varredura de 5 a 500 mV / s. Os CVs de CNFs em uma ampla gama de taxas de varredura são próximos ao formato de uma caixa, sem qualquer protuberância, ou o desvio indica características claras de camada dupla e alta reversibilidade. Os CVs para CA mostram uma corrente muito mais alta do que os CNFs. Em taxas de varredura baixas, o formato do CV é retangular, apresentando que a resposta do eletrodo na carga e na descarga é altamente reversível. No entanto, em taxas de varredura mais altas, o CV se desvia de uma forma retangular. Pode haver várias razões possíveis relacionadas a este desvio, (1) devido à baixa condutividade elétrica da estrutura porosa da CA de poros internos que não são acessíveis aos íons e (2) constante de tempo diferente de zero e corrente transitória elevada, resultando em um capacitor mais longo tempo de carga e um colapso da forma retangular [21, 22].

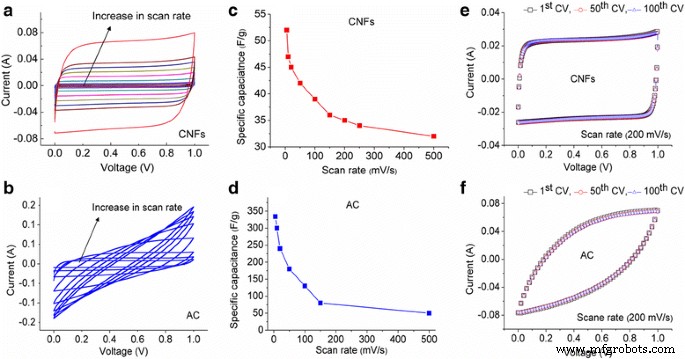
a , b CVs de CNFs e AC, respectivamente, a taxas de varredura de 5, 10, 20, 50, 100, 150 e 500 mV / s; c , d comparação de capacitância específica em diferentes taxas de varredura; e , f CVs de CNFs e AC, respectivamente, do 1º ao 100º ciclo

A Figura 4c, d apresenta a comparação de capacitância específica de CNFs e CA de taxas de varredura de 5 a 500 mV / s. Como pode ser visto na Fig. 4c, os CNFs mostram a capacitância específica mais alta 52 F / g a uma taxa de varredura de 5 mV / s. A capacitância específica diminuiu para 32 F / g a uma taxa de varredura de 500 mV / s. Esses resultados indicam a diminuição moderada na capacitância específica, e em taxas de varredura ainda mais altas, a maior parte da área de superfície e poros dos CNFs são acessíveis aos íons. A capacitância de AC diminui de 334 para 50 F / g para 5 a 500 mV / s Fig. 4d. Uma capacitância específica muito alta a uma taxa de varredura baixa se deve ao fato de os íons terem tempo suficiente para penetrar profundamente na estrutura microporosa (menos de 2 nm) da CA. Pode-se presumir que em taxas de varredura mais altas, principalmente os mesoporos de poros maiores (2–50 nm) estão contribuindo para a capacitância. Isso se deve principalmente à diferença na taxa de difusão do eletrólito nos poros de diferentes tamanhos e também devido à conexão de rede entre poros grandes e pequenos [23]. Conforme discutido por A.G. Pandolofo et al., A área de superfície medida é contribuída por todos os poros abertos, mas todos os poros não são eletroquimicamente acessíveis [8].

A maior capacitância específica de AC em comparação com CNFs pode ser devido à maior área de superfície, que resulta no aumento das áreas acessíveis para íons eletrólitos para armazenamento de carga dentro de poros relativamente pequenos.

As curvas CV dos CNFs e AC (Fig. 4e, f) indicam comportamento de capacitância estável medido até o 100º ciclo a uma taxa de varredura de 200 mV / s. O 100º ciclo CV para ambas as amostras mantém a forma como era para o primeiro ciclo sugere excelente estabilidade e processos de eletrodo reversíveis.

O desempenho supercapacitivo de CNFs e AC foi ainda comparado por GCD como mostrado na Fig. 5a, b. A capacitância de descarga ( C ) é estimado a partir da inclinação ( dV / dt ) da porção linear da curva de descarga usando a Eq. 3
$$ {C} _ {\ mathrm {s}} =\ left (\ frac {2I} {\ left (dV / dt \ right) .m} \ right) $$ (3)
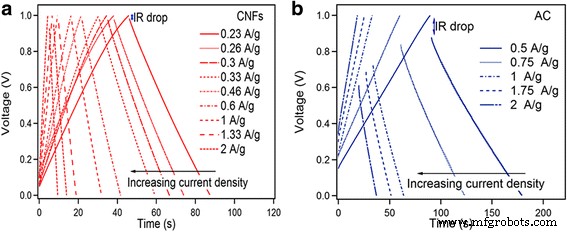
a Curvas GCD em diferentes densidades de corrente de CNFs. b Curvas GCD em diferentes densidades de corrente de AC

Onde C _s é a capacitância específica em F / g, ∆V é a diferença de tensão durante a curva de descarga em V , eu é a corrente em A e ∆t é o tempo de alta em s .

Pode-se observar que os processos de carga e descarga são quase simétricos, indicando excelente reversibilidade eletroquímica dos eletrodos. As curvas de descarga de CNFs mostram um pequeno IR queda implicando uma pequena resistência em série equivalente, que é essencial para a característica de potência dos supercondensadores. O menor IR queda de CNFs para o AC é devido à alta condutividade dos CNFs. O grande IR queda para AC significa maior resistência em série equivalente (ESR). A capacitância específica calculada para CNFs 23,8 F / g a 0,23 A / g diminui para 19 F / g a 2 A / g. A capacitância específica de AC diminui de 159 F / g na densidade de corrente 0,5 A / ge 139 F / g a 2,5 A / g Fig. 6a. A capacitância específica de ambos os capacitores simétricos de CNFs e AC diminui com o aumento da densidade de corrente, que é muito comum para supercapacitores e é causada principalmente pela limitação de difusão de íons eletrolíticos nos micrósporos do eletrodo.

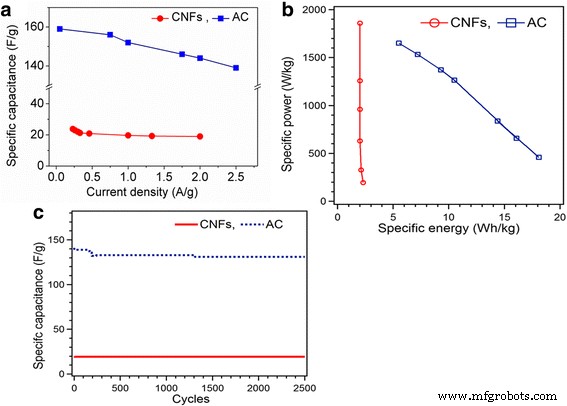
a Comparação de capacitância específica da curva de descarga de GCD. b Gráfico de Ragone de potência específica contra energia específica para CNFs e AC. c Estabilidade de ciclagem de CNFs e AC

O poder específico, P , e a energia específica, E, entregue na descarga foram estimadas pelas Eqs. (4) e (5).
$$ P =\ raisebox {1ex} {$ Vi $} \! \ Left / \! \ Raisebox {-1ex} {$ m $} \ right. $$ (4) $$ E =\ raisebox {1ex} {$ Vit $} \! \ Left / \! \ Raisebox {-1ex} {$ m $} \ right. $$ (5)
Onde V é a voltagem excluindo IR cair, i é a corrente de descarga e t é a hora [24].

Como pode ser visto no gráfico de Ragone Fig. 6b, o eletrodo CNF mostra uma energia específica máxima de 2,3 Wh / kg a uma potência específica de 197 W / kg e uma densidade de potência máxima de 1860 W / kg a uma energia específica de 2 Wh / kg indicando suas boas características de potência. Esses resultados mostram um aumento da potência específica; a energia específica diminui apenas um pouco, o que é uma assinatura de excelentes propriedades eletroquímicas de alta densidade de energia e potência de saída, portanto, muito promissoras para aplicação em cenários onde tanto alta potência de saída como alta capacidade de energia são necessárias [25]. Para CA com o aumento da potência específica de 459 para 1650 W / kg, a energia específica diminuiu de 18,1 para 5,5 Wh / kg.

A estabilidade do ciclismo também é um fator vital para aplicações práticas. A medição do ciclo de carga-descarga galvanostática foi realizada a uma densidade de corrente constante 2 A / g para CA e para CNFs até 2500 ciclos Fig. 6c. O comportamento da CA durante a estabilidade do ciclo mostra uma pequena diminuição na capacitância de 141 para 131 F / g em 2.500 ciclos. Esse resultado expressa que o desvanecimento da capacitância é devido às reações irreversíveis no início da ciclagem [10]. As medições de ciclo CNF revelam excelente retenção de capacitância 19 F / g em 2.500 ciclos.

O supercapacitor foi posteriormente analisado por espectroscopia de impedância eletroquímica (EIS). Ele representa o gráfico de Nyquist na faixa de frequência de 10 kHz – 0,1 Hz para CNFs e AC (Fig. 7a). Os gráficos de Nyquist consistem em (1) uma interceptação de alta frequência no eixo Z 'real, (2) um semicírculo na região de alta a média frequência e (3) uma linha reta em uma frequência muito baixa região [26]. Na região de alta frequência, as interceptações com Z 'de CNFs e AC são 0,11 e 0,16 Ω, respectivamente. Este valor é considerado como a resistência elétrica total do material do eletrodo, eletrólito e contatos elétricos [27]. O semicírculo de alta a média frequência corresponde à combinação paralela de resistência de transferência de carga ( R _ct ) e capacitância de camada dupla [28]. Pode ser visto que semicírculo ( R _ct ) é maior para AC (3,56 Ω) do que para CNFs (0,17 Ω). Os ESRs calculados foram 0,28 e 3,72 Ω para CNFs e AC, respectivamente. O valor muito pequeno de ESR para CNFs, em relação a AC, indica o fácil transporte / difusão de elétrons e íons nos eletrodos CNF. Isso indica que o eletrodo CNF tem condutividade muito maior do que o eletrodo AC. Conforme também observado na Fig. 7a, os CNFs apresentaram maior inclinação da reta, na faixa de baixa frequência, do que a CA. Isso significa que os CNFs apresentam um comportamento capacitivo mais alto do que o AC.

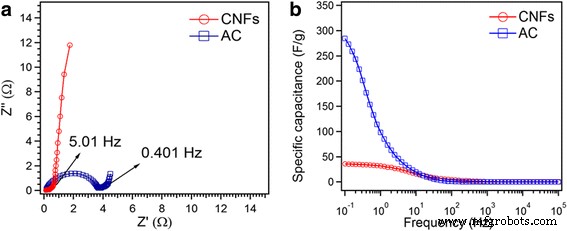
a Gráfico de Nyquist de CNFs e AC. b Comparação Csp calculada a partir de EIS.

A capacitância específica, C _s , do supercapacitor CNF e AC também foi calculado a partir da análise de impedância empregando o componente imaginário da impedância seguindo a equação [29].
$$ {C} _ {\ mathrm {s}} =4 \ left (- \ left (1/2 \ pi f {z} ^ {\ prime \ prime} m \ right) \ right) $$ (6)
Onde f é a frequência em Hz, z ”É o componente imaginário da impedância, e m é a massa de CNFs ou AC calculada para um eletrodo. A Figura 7b mostra a mudança mais alta na capacitância específica de CNFs e AC abaixo da frequência de 10 Hz. A capacitância específica obtida para CNFs (36 F / g) e AC (284 F / g) na frequência de 0,1 Hz é praticamente comparável à capacitância calculada por CV. Na verdade, a maior capacitância específica para CA é devido à maior área de superfície disponível para carga acumulada na interface sólido-líquido.

Constante de tempo τ é a propriedade do supercapacitor que reflete a resposta do dispositivo. Um pequeno valor de τ dá indicação de uma melhor resposta. A constante de tempo τ foi calculado usando a seguinte equação:
$$ 2 \ tau =\ frac {E _ {\ mathrm {D}}} {P _ {\ mathrm {D}}} $$ (7)
Onde E _D é a densidade de energia e P _D é a densidade de potência. E _D e P _D foram calculados usando as seguintes equações:
$$ {E} _ {\ mathrm {D}} =0,5C {V} ^ 2 / m $$ (8) $$ {P} _ {\ mathrm {D}} ={V} ^ 2/4 \ esquerda (\ mathrm {ESR} \ direita) m $$ (9)
Onde V é a janela de tensão durante a curva de descarga de carga, C é a capacitância da carga-descarga e ESR calculada a partir da espectroscopia de impedância, e m é a massa do eletrodo. A constante de tempo calculada τ para AC foi de 3,1 se para CNFs foi de 0,08 s para densidade de corrente 2 A / g, indicando uma melhor resposta capacitiva para CNFs.

A relação entre Z _real e a frequência nos dá informações sobre o eletrólito e a resistência de transferência de carga no eletrólito da Fig. 8a. O comportamento da resistência do eletrodo é muito influenciado pela natureza do eletrodo de carbono. Para ambos os CNFs e AC em alta frequência 100 KHz, ESR está em seus valores mais baixos na ordem de cerca de 0,1 Ω, que apresenta a resistência do eletrólito R s. Com a diminuição da frequência, até 506 Hz, há um aumento acentuado na resistência de AC em relação aos CNFs. Na frequência mais baixa observada (0,1 Hz), o ESR apresentou um valor de 1,87 e 4,5 Ω para AC e CNFs, respectivamente. O aumento da VHS com a diminuição da frequência pode ser devido à dificuldade de penetração do sinal elétrico nos poros mais profundos (preenchidos com eletrólito) e / ou nas partículas menores [30]. Essa variação pode ser justificada pelo fato de que à medida que a frequência diminui, os íons podem atingir facilmente as zonas mais profundas dos poros do carvão ativado e, consequentemente, seu maior deslocamento dentro do eletrólito resulta em maior resistência do eletrólito [31].

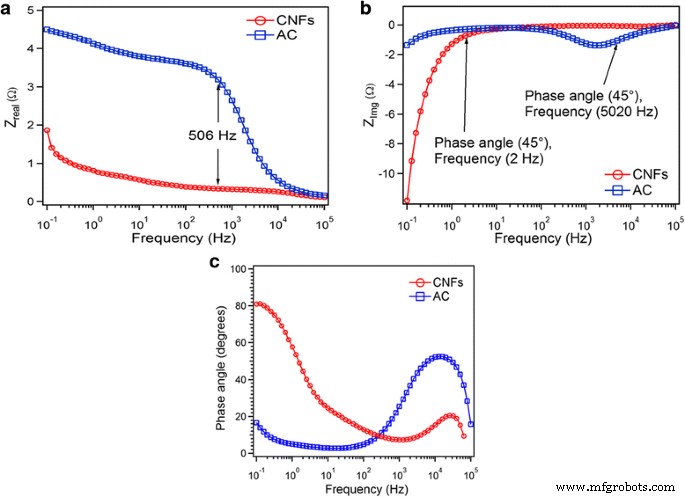
a O real e b partes imaginárias são plotadas em função do log de frequência e c mudança de fase em função da frequência para AC e CNFs

A relação entre Z _Img e a frequência nos dá informações sobre o tempo de relaxamento ( τ ₀ ) na região limite, onde o supercapacitor é transferido do resistor para o capacitor Fig. 8b. A constante de tempo τ ₀ que corresponde ao ângulo de fase de 45 ° representa a transição do capacitor eletroquímico de um comportamento puramente resistivo para puramente capacitivo. É bem sabido que maior entrega de potência corresponde a menor τ ₀ valores. Para frequência, f> 1 / τ ₀ , ele atua como um resistor puro e para f <1 / τ ₀ , ele se comporta como um capacitor puro. O ângulo de fase de 45 ° foi encontrado para AC na frequência 5020 Hz e para CNFs em 1,99 Hz. Isso mostra que o tempo de relaxamento para AC é muito menor do que para CNFs. Conseqüentemente, o comportamento resistivo da tradução para o comportamento capacitivo para AC é muito mais rápido do que CNFs.

A Figura 8c representa a variação do ângulo de fase em função da frequência, que é conhecido como gráfico de Bode. Os ângulos de fase são - 20 ° e - 88 ° em baixa frequência 0,1 Hz nos sistemas AC e CNF, respectivamente (Fig. 8c). Em geral, a abordagem do ângulo de fase de -90 ° confirma o melhor desempenho capacitivo e o rápido processo de carga-descarga. A constante de tempo de relaxamento, τ 0, define o tempo necessário para entregar a carga armazenada de forma eficaz, conforme visto na Fig. 8b [32].

Efeito da estrutura do carbono e da textura porosa no desempenho do EDLC

A partir da caracterização eletroquímica, é evidente que o supercapacitor baseado em eletrodos AC dá uma capacitância específica mais alta do que os CNFs no eletrólito 6-M KOH. De acordo com a equação, ∁ =∈ A / d , distância ( d ) é muito pequeno quando o eletrodo contém microporos. A maior capacitância de AC é devido a algumas propriedades importantes, essas são a maior área de superfície BET e a existência de mais de 88% de ultramicroporos e microporos. Já as amostras de CNF apresentam baixa área de superfície BET e 17,9% de microporos. Outro fator importante que influencia a capacitância está relacionado à seguinte equação, τ = L ² / D . Onde L refere-se ao comprimento de transporte de íons, e D refere-se ao coeficiente de transporte de íons. De acordo com essa equação, os íons entram rapidamente nos microporos, mas conforme o tamanho dos poros aumenta, a área externa também aumenta. Devido a este fato, os íons se acumulam fora dos poros, resultando na diminuição da capacitância. Segundo E. Raymundo-Pinero et al., Em solução aquosa, a formação de camada dupla é muito favorável quando o tamanho dos poros está em torno de 0,7 nm [19]. Nossos resultados revelam que o tamanho de poro de AC (0,47 nm) está na faixa ideal para construir a camada dupla, portanto, apresenta maior capacitância específica sobre CNFs.

Conclusões

Eletrodos CNF e AC foram preparados em uma técnica semelhante e comparados como supercapacitor simétrico usando solução aquosa. A distribuição do tamanho dos poros, a área de superfície do eletrodo e a resistência total do eletrodo desempenham um papel crucial na determinação do desempenho do supercapacitor. Os resultados de BET revelam que AC tem um alto número de microporos e estrutura ultramicroporosa que dá uma área de superfície de 1042 m ² / g, enquanto o eletrodo CNF contém estrutura mesosporosa dominante e área de superfície 83 m ² / g. Devido a isso, o material AC fornece uma capacitância específica (334 F / g) muito maior do que os CNFs (52 F / g). De fato, uma capacitância específica mais alta para CA deu uma energia específica mais alta (18,1 Wh / kg) do que para CNFs (2 Wh / kg). Por outro lado, os CNFs revelam menor ESR (0,28 Ω) do que AC (3,72 Ω). As potências específicas obtidas dependendo do valor ESR foram 1860 e 450 W / kg para CNFs e AC, respectivamente. Portanto, a CA é considerada adequada para aplicações de energia. Visto que o CNF é o melhor candidato para aplicações de energia.

O precursor de titânio ideal para a fabricação de camada compacta de TiO2 para células solares de perovskita Adepto verde na síntese e estabilização de nanopartículas de cobre:​​atividades catalíticas, antibacterianas, citotoxicidade e antioxidantes