Estabilidade da forma de nanoplacas metálicas:um estudo de dinâmica molecular

Resumo

Nanoplacas metálicas têm atraído interesses generalizados devido à sua versatilidade funcional, que depende muito de suas morfologias. Neste estudo, a estabilidade da forma de várias nanoplacas metálicas com redes cúbicas centradas no corpo (bcc) é investigada através do emprego de simulações de dinâmica molecular. Verificou-se que a nanoplaca com (110) planos de superfície é a mais estável em comparação com aquelas com (111) e (001) superfícies, e suas formas evoluem com padrões diferentes à medida que a temperatura aumenta. A formação de facetas com orientação diferente é observada nas nanoplacas (001), o que leva ao acúmulo de tensão de cisalhamento e, portanto, resulta na subsequente formação do formato de sela. A evolução da forma associada é caracterizada quantitativamente. Outras simulações sugerem que a estabilidade da forma pode ser ajustada por orientações de faceta, tamanhos de nanoplacas (incluindo diâmetro e espessura) e componentes.

Introdução

Como uma classe importante de nanomateriais funcionais, as nanoplacas metálicas têm sido extensivamente sintetizadas e examinadas devido às suas excelentes atividades em catálise [1,2,3,4], propriedades ópticas ajustáveis [1, 5,6,7], potencial utilização em microcircuitos , entre outros [8, 9]. Como é bem sabido, o desempenho de aplicação dos nanomateriais depende fortemente de suas estruturas e morfologias. Portanto, uma compreensão aprofundada da estabilidade da forma dessas nanoplacas metálicas deve ser uma questão de importância crucial para a sua síntese e uso. Do ponto de vista da termodinâmica, a estrutura de uma única nanoplaca se desvia do mínimo energético e deve se desenvolver em uma nanopartícula esférica devido à tendência de minimizar sua energia superficial. Porém, como configurações metaestáveis, as nanoplacas não são raramente observadas em experimentos devido à participação de fatores cinéticos complexos [10]. Temperatura relativamente mais alta aumenta a possibilidade de o sistema escapar do aprisionamento cinético e realizar o estado com menor energia. Especialmente para aquelas nanoplacas com espessuras tão finas quanto várias camadas atômicas, as proporções superfície-volume significativamente altas implicam em uma grande proporção de átomos com ligação fraca (ou seja, alta mobilidade), que são sensíveis ao ambiente e, portanto, são presumivelmente fáceis para induzir a mudança de forma. Induzidas pelas condições externas ajustadas, as transformações de forma e estrutura foram observadas para ocorrer no regime sólido [11,12,13,14,15]. Observe que este tipo de transformações não é exclusivamente determinado pela termodinâmica para se desenvolver em direção às esferas mais energeticamente favorecidas, enquanto o caminho reverso das partículas esféricas para as placas anisotrópicas, semelhante ao amadurecimento de Ostwald, também foi descoberto como sendo desencadeado pela energia térmica tratamento [11].

Investigações experimentais foram realizadas para examinar as propriedades térmicas de nanoplacas metálicas. Por exemplo, os resultados do microscópio eletrônico de transmissão (TEM) in situ combinados com outras análises estruturais mostram que as nanoplacas de Au apresentam (110) facetas em torno das bordas consistindo nos átomos mais instáveis, e a fragmentação ocorre durante o aquecimento [15]. No entanto, o experimento microscópico acha extremamente difícil fornecer caracterizações quantitativas do mecanismo de evolução da forma. Alternativamente, a simulação de dinâmica molecular (MD), como ferramenta ideal, pode apresentar imagens diretas sobre as transformações de forma na resolução do nível atômico. Consequentemente, realizamos os cálculos de MD em nanoplacas metálicas para divulgar seus mecanismos de mudança de morfologia, descrevendo o processo de curvatura e flambagem envolvido. Metais com reticulados cúbicos centrados no corpo (bcc) são abordados porque o entendimento relevante sobre sua estabilidade de forma ainda está faltando, apesar de sua existência comum em experimentos [16]. Este estudo serve de referência tanto para a síntese quanto para as aplicações dessas nanoplacas metálicas.

Métodos

Nanoplacas de ferro (Fe) com redes bcc (constante de rede a =2,8665 Å), que são compostos por três camadas atômicas (o diâmetro d =32 a na maioria dos casos), foram primeiro modelados. Inicialmente, suas superfícies são, respectivamente, definidas para serem diferentes planos de baixo índice, incluindo (111), (001) e (110). Além disso, outras nanoplacas metálicas bcc, como W, Nb, Mo e Cr, também foram construídas em conformidade. Esses modelos foram criados por meio de comandos do pacote MD LAMMPS [17].

As interações interatômicas foram descritas pelos potenciais correspondentes do método do átomo incorporado (EAM) [18,19,20,21,22]. Os modelos iniciais foram primeiro quase estaticamente relaxados para um estado de energia mínima local através do método do gradiente conjugado (CGM). Após o relaxamento completo, o aquecimento contínuo foi simulado em um ensemble canônico (NVT) usando LAMMPS, e as quantidades de estado (energia e tensor de tensão) são exportadas de forma correspondente. A temperatura foi ajustada para aumentar de 1 a 300 K (ou mais) com um incremento de 1 K. Sob um intervalo de tempo de 2 fs, o tempo de relaxamento de 200 ps em cada temperatura é empregado, e as quantidades estatisticamente médias são retiradas do últimos 8 ps. A incerteza das simulações vem principalmente de dois aspectos:a precisão dos potenciais e a convergência da energia a cada temperatura. Observe que os potenciais que usamos foram amplamente adotados em simulações moleculares e verificados repetidamente [23,24,25,26,27], em média, enquanto 200 ps é examinado como suficiente para permitir que o sistema alcance seu equilíbrio térmico, acreditamos, portanto, que nosso as simulações são confiáveis.

Além disso, o tensor de tensão local do i _th átomo foi calculado por
$$ {\ sigma} _ {\ alpha \ beta} =\ frac {1} {2 {\ Omega} _i} \ sum \ limits_ {j \ ne i} {F} _ {ij} ^ {\ alpha} { R} _ {ij} ^ {\ beta}, $$
em que α e β poderia ser x , y e z ; F _ij e R _ij são a força e a distância entre os átomos i e j , respectivamente [28]. Ω _i é o volume local que pode ser identificado com o volume do poliedro de Voronoi construído pelos planos perpendiculares que dividem as linhas entre os átomos i e todos os seus átomos vizinhos, que foram calculados através do método de volumes iguais [29].

Resultados e discussão

Conforme a temperatura aumenta, as morfologias das três nanoplacas de Fe evoluem com padrões diferentes. Os gráficos superiores no painel esquerdo da Fig. 1 exibem suas energias potenciais dependentes da temperatura ( E _p ) Para as três nanoplacas, os planos de cristal com diferentes índices de Miller levam a uma hierarquia clara na estabilidade estrutural. De acordo com os cálculos, as energias potenciais médias por átomo (não mostradas na Fig. 1) são - 2,833, - 3,457 e - 3,668 eV / átomo respectivamente para as configurações iniciais com (111), (001) e (110) superfícies. Considerando que as nanoplacas são tão finas quanto três camadas atômicas, é natural descobrir que seus valores de energia estão na mesma ordem das energias de superfície dos três planos de cristal correspondentes (2,58, 2,47 e 2,37 J / m ² para as superfícies (111), (001) e (110), respectivamente [30]). Com energias potenciais distintamente mais altas, as nanoplacas com planos de cristal planos (111) e (001) não são capazes de manter suas estruturas iniciais conforme construídas. Eles imediatamente se transformam em estados metaestáveis com superfícies curvas (cf. instantâneos (a) e (b) no painel direito da Fig. 1). Em contraste, a nanoplaca (110) apresenta a melhor estabilidade estrutural. Sua morfologia (ver Fig. 1c) permanece invariante ao longo de toda a região de temperatura examinada, o que pode ser corroborado pelo aumento constante da energia com uma tendência linear. Já para as outras duas nanoplacas, suas deformações de forma exibem características diferentes. A nanoplaca menos estável (111) se transforma em uma forma irregular instantaneamente após o relaxamento (ver Fig. 1a), e essa geometria irregular facilita o progresso do encolhimento em uma partícula compacta. Portanto, sua energia potencial diminui periodicamente e finalmente atinge um nível muito inferior ao da nanoplaca (001). No entanto, a superfície de sela da nanoplaca (001) demonstrada na Fig. 1b retém até se tornar uma partícula irregular em cerca de 200 K. A evolução desta estrutura com estabilidade estrutural média é acompanhada por uma mudança de energia relativamente moderada, que pode ser dividida em quatro estágios demarcados por linhas pontilhadas nos gráficos de energia potencial.

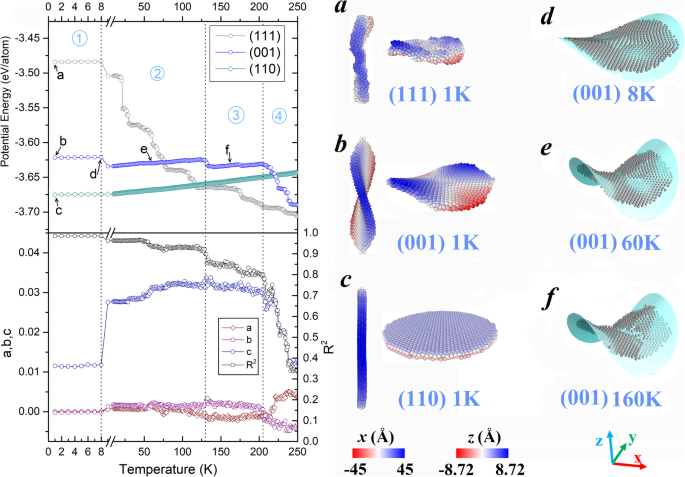
Painel esquerdo:evolução da temperatura da energia potencial de três nanoplacas (gráficos superiores), e os parâmetros geométricos obtidos pelo ajuste da camada intermediária da nanoplaca (001) (gráficos inferiores); Painel direito: a , b , c Instantâneos de três nanoplacas após o relaxamento. d , e , f Instantâneos da camada intermediária na nanoplaca (001) tirados em temperaturas representativas. As superfícies ciano denotam os resultados de ajuste correspondentes

Para investigar quantitativamente a variação da morfologia, ajustamos a camada intermediária da nanoplaca (001) pela equação da superfície quádrica z =A x ² + B y ² + C xy + D. Os resultados do ajuste são fornecidos abaixo dos gráficos de energia na Fig. 1, em que a, b e c são os parâmetros geométricos na equação, e R ² refere-se ao coeficiente de determinação. R ² indica o grau de ajuste, e seu valor ideal é igual a 1. De acordo com as variações de energia, as transições correspondentes desses parâmetros de ajuste também são observadas nos pontos críticos entre os diferentes estágios. As temperaturas críticas são identificadas como 8, 129 e 205 K. Durante as primeiras três fases, o valor de R ² permanece superior a 0,8, implicando que a nanoplaca (001) mantém aproximadamente sua forma de sela. Uma vez que o parâmetro c é obviamente maior do que aeb, as duas seções elevadas da nanoplaca são orientadas ao longo da direção [110]. Enquanto isso, o valor de c aumenta significativamente após o primeiro estágio, o que sugere a superfície incrivelmente curvada para cima. Esta tendência pode ser claramente percebida a partir dos instantâneos representativos na Fig. 1d-f, que são respectivamente tirados em 8, 60 e 160 K. Cada deformação de flexão puxa o sistema para fora de seu estado metaestável anterior e resulta em uma ligeira queda no energia potencial. Esses pequenos ajustes de forma e energia terminam em 205 K, de onde começa o quarto estágio e a superfície de sela original gradualmente colapsa em uma partícula irregular com ainda mais energia minimizada.

Para examinar o mecanismo de deformação da nanoplaca (001) em detalhes, investigamos os arranjos atômicos e a distribuição de tensões. Após o relaxamento a 1 K, a energia potencial da nanoplaca é liberada em grande parte pela curvatura da estrutura ao longo da direção [110], como discutido acima. Durante a formação deste estado metaestável, nenhuma difusão entre camadas de átomos é observada. A Figura 2a apresenta a visão vertical de sua superfície superior. Observe que a situação nas outras duas camadas atômicas se assemelha essencialmente à descrita a seguir. A partir da análise da estrutura da rede, a maioria dos átomos (exceto os coloridos em branco) são identificados para formar (110) facetas, ou seja, a rede inicial (001) se transforma na estrutura mais compacta no cristal bcc e ocorre a reconstrução . Na Fig. 2a, os átomos nas facetas adjacentes são atribuídos a cores diferentes. A célula unitária de cada faceta é rotulada por um retângulo verde, no qual a linha amarela curta indica sua respectiva direção [110]. Como pode ser visto, essas (110) facetas, que são esquematicamente ilustradas no canto inferior direito da Fig. 2a, estão dispostas em diferentes orientações. A distribuição é aproximadamente simétrica. Tome um quarto da superfície total como exemplo, as facetas 1 e 2 basicamente se alinham em paralelo e são aproximadamente perpendiculares às facetas 4 e 5. Os átomos na faceta 3 são ligeiramente distorcidos para acomodar as redes de ambas as facetas 1 e 2

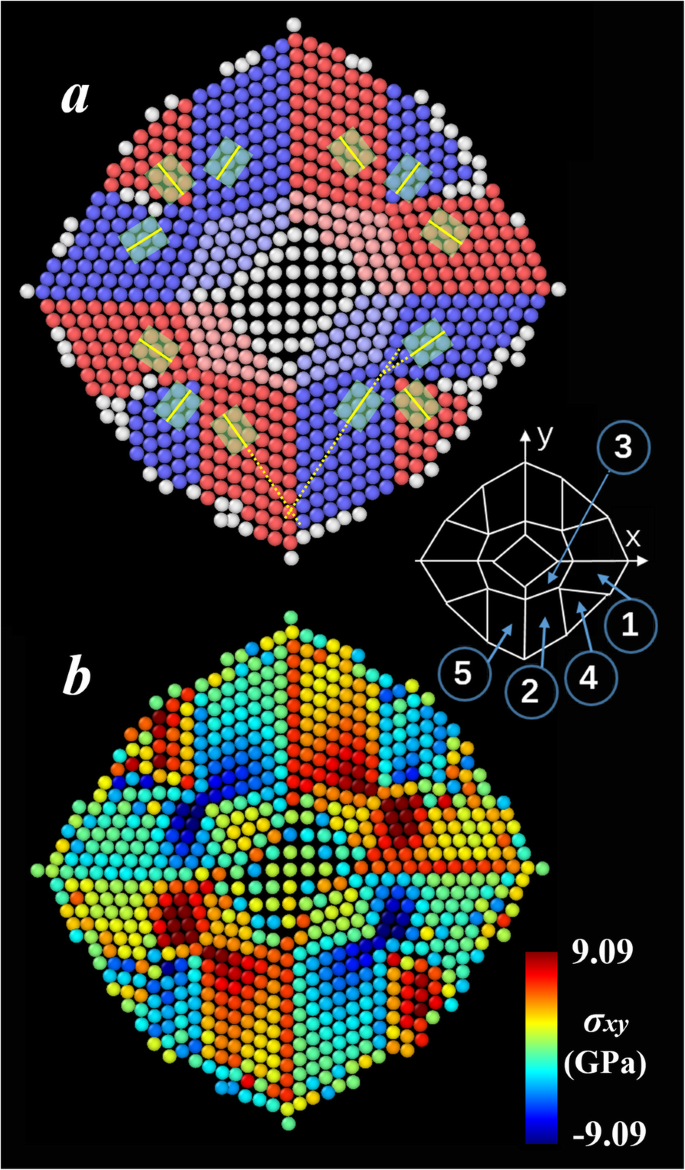
a Instantâneo da superfície superior de (001) nanoplaca após relaxamento a 1 K e b a distribuição de tensão de cisalhamento correspondente

A partir da análise da tensão calculada na nanoplaca, verifica-se que a tensão de cisalhamento apresenta uma correlação aparente com a deformação, o que a diferencia dos demais componentes do tensor de tensão. Portanto, consideramos a tensão de cisalhamento como a principal força motriz da deformação de flexão e apresentamos sua distribuição na Fig. 2b. Claramente, a tensão não é mais uniformemente distribuída devido à ordem de curto alcance induzida pelo surgimento dessas (110) facetas. A partir da comparação das Fig. 2 aeb, verifica-se que a distribuição de tensões está altamente correlacionada com o arranjo de orientação das facetas. As tensões nas facetas vermelhas mostradas na Fig. 2a são geralmente positivas, enquanto são negativas nas azuis. Esta observação sugere que as facetas vermelha e azul tendem aproximadamente a se mover em direções opostas. Observou-se a existência de lacunas de tensão significativas perto dos limites dos grãos. Essas tensões acumuladas são acompanhadas pela formação de (110) facetas e seriam liberadas por meio de deformação adicional da nanoplaca.

A Figura 3 mostra duas transformações críticas durante a deformação subsequente da nanoplaca (001). Para ser consistente com a Fig. 2, ilustramos apenas os átomos da camada superior. As distribuições de tensões e coordenadas Z são apresentadas. Como pode ser visto na Fig. 3a, a distribuição de tensões em 8 K assemelha-se à situação em 1 K (cf. Fig. 2b), e a flexão existe (cf. Fig. 3c e Fig. 1d). Quando a temperatura aumenta para 9 K, a curvatura se desenvolve significativamente, como pode ser visto na Fig. 3d. Enquanto isso, pode-se descobrir que as lacunas de tensão originalmente formadas desaparecem (comparando as Fig. 3 a e b). A liberação da tensão de cisalhamento é resultado dessa deformação por flexão adicional. Consequentemente, a energia potencial diminui (cf. Fig. 1), e a nanoplaca evolui para um estado mais estável. Quanto à segunda transição mostrada na Fig. 3, ela começa em 129 K e termina em 134 K, experimentando uma faixa de temperatura mais ampla. Observe que após a transição ocorrendo a 9 K, uma tensão positiva consideravelmente grande ainda existe na área intermediária da superfície (cf. Fig. 3b). Na verdade, esse estado de tensão se mantém durante todo o segundo estágio do processo de mudança de forma (9-129 K) (cf. Fig. 3e). Da mesma forma, é também a força motriz da transição seguinte. Posteriormente, como visto na Fig. 3f, os átomos vermelhos na Fig. 3e tornam-se verdes (ou azuis), indicando que a tensão positiva existente foi liberada. Com o propósito de destacar a transformação da forma que ocorre entre 129 e 134 K, apenas metade dos átomos na superfície superior são exibidos na Fig. 3 g e h, em que a caixa verde destaca a área alterada. A região na caixa verde dobra em direção a - Z direção, levando ao desvio da forma de sela anterior. Este desvio também pode ser confirmado pela queda óbvia de R ² valor na Fig. 1.

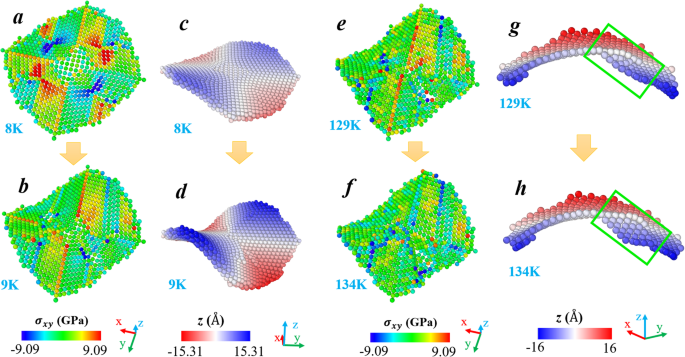
Duas transformações críticas durante a evolução da temperatura da nanoplaca (001). Para cada estado, os átomos são coloridos respectivamente de acordo com a , b , e , f seus valores de tensão de cisalhamento e c , d , g , h Z coordenadas

Conforme discutido acima, a transformação da forma da nanoplaca (001) é conduzida pela tensão de cisalhamento, cuja distribuição depende fortemente do arranjo de rede. A fim de exemplificar ainda mais a possibilidade de adaptar a morfologia através do projeto de orientação cristalina, modelamos uma nanoplaca de átomos de três camadas (110), em que cada camada é dividida em quatro facetas orientadas diferentes, conforme demonstrado na Fig. 4a (referido como "Nanoplaca modulada (110)" a seguir). As linhas laranja na ilustração esquemática indicam suas respectivas [110] direções. Para facilitar a comparação, mostramos a nanoplaca regular (110) na Fig. 4d. Para a configuração inicial, a energia potencial calculada da nanoplaca modulada (110) é igual a - 3,617 eV / átomo, maior que o valor correspondente da nanoplaca regular (110) (- 3,668 eV / átomo) devido à existência de energia interfacial. Em contraste com o padrão uniforme de distribuição de tensão de cisalhamento da nanoplaca regular (110) (cf. Fig. 4e), lacunas de tensão notáveis aparecem entre facetas adjacentes na Fig. 4b. Essas lacunas são especialmente significativas entre os átomos localizados perto dos limites dos grãos. Após o relaxamento a 1 K, a região com gradiente de tensão se estende para envolver mais átomos ao redor dos limites, como pode ser visto na Fig. 4c. Enquanto isso, a energia potencial média cai para - 3,653 eV / átomo, e a curvatura da configuração resulta em uma placa de sela, semelhante à nanoplaca (001). Como a temperatura é continuamente elevada, durante a evolução da forma da nanoplaca modulada (110), três estágios podem ser identificados com 179 e 277 K como os pontos críticos. No primeiro estágio, a forma da sela basicamente se mantém apesar de pequenas flutuações, como exemplificado no instantâneo de inserção de 100 K. No entanto, após a transição ocorrendo em 179 K, a configuração volta a ser semelhante a um disco e mantém esta forma sem mudança óbvia ao longo da segunda fase (ver, por exemplo, o instantâneo inserido de 200 K). Em torno do ponto crítico (179 K), observe que a parte elevada no centro combinada com o plano da superfície fragmentada ainda corresponde à configuração com menor energia. Finalmente, quando a temperatura atinge 277 K, o sistema começa a encolher para uma partícula irregular (cf. o instantâneo inserido de 300 K), levando à redução radical na energia potencial, semelhante ao quarto estágio da nanoplaca (001) descrita mais cedo. Observe que a energia potencial da nanoplaca regular (110) começa a diminuir drasticamente a 552 K (os pontos de dados correspondentes não são inteiramente apresentados na Fig. 1), a nanoplaca modulada (001) mostra uma estabilidade de forma significativamente diminuída. Esses resultados indicam que o projeto de orientações cristalinas é uma abordagem eficiente para modular a estabilidade da forma.

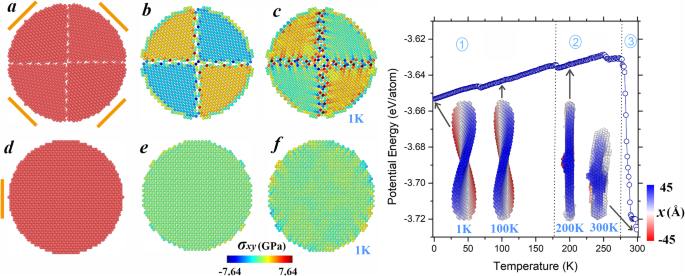
Painel esquerdo:ilustração esquemática de a a nanoplaca modulada (110) e d o normal. b , c , e , f Exiba, respectivamente, suas distribuições de tensão de cisalhamento nas configurações iniciais e em 1 K. Painel direito:Energias potenciais dependentes da temperatura da nanoplaca modulada (110). Os instantâneos nas inserções são tirados em temperaturas representativas

Para obter uma compreensão abrangente dos padrões de evolução da forma, consideramos nanoplacas de Fe (001) bcc com diâmetros diferentes (incluindo d =12 a , 40 a , e 50 a ) Suas energias potenciais e configurações típicas durante o processo de aquecimento são mostradas na Fig. 5. Observe que a nanoplaca mencionada com d =32 a também é mostrado para comparação. Com energia potencial relativamente alta, a menor nanoplaca experimenta mais estágios em comparação com as outras. Como pode ser visto no instantâneo da Fig. 5a, a nanoplaca com o diâmetro de 12 a mantém suas superfícies planas (a) até que a flexão comece a ocorrer em 52 K (b) e, finalmente, a forma de sela se forma em 62 K (c). No entanto, esta estrutura de sela não dura em uma ampla faixa de temperatura, e a seguinte difusão entre camadas acontece a 84 K, levando a uma diminuição acentuada na energia potencial. A nanoplaca espessada, exemplificada na Fig. 5 (d), mantém sua característica até que uma concentração adicional apareça em cerca de 200 K. Quanto à nanoplaca com d =40 a , a forma de sela é mantida de forma estável em temperaturas que variam de 1 a 190 K antes de colapsar em uma partícula compacta. No caso da nanoplaca com d =50 a , a forma de sela permanece até 134 K (indicada pela seta no ponto “g”) e então se distorce para uma estrutura irregular, conforme ilustrado na Fig. 5f. Como pode ser visto, a 190 K, onde a nanoplaca com d =40 a apenas começa a entrar em colapso, aquele com d =50 a já completou sua transformação de forma de sela em irregular. Estas observações sugerem que, à medida que o diâmetro aumenta de 12 a a 40 a , a faixa de temperatura em que a forma da sela poderia ser estável gradualmente se torna mais ampla; no entanto, quando o diâmetro continua crescendo (para 50 a , por exemplo), a estabilidade da forma de sela diminui até certo ponto. Ou seja, embora um diâmetro maior leve a uma melhor estabilidade estrutural (menor energia potencial no estado fundamental), não é o único fator determinante a afetar a estabilidade, a influência de outros aspectos (como efeitos cinéticos e de entropia) também desempenha um papel importante, especialmente quando a nanoplaca é grande o suficiente.

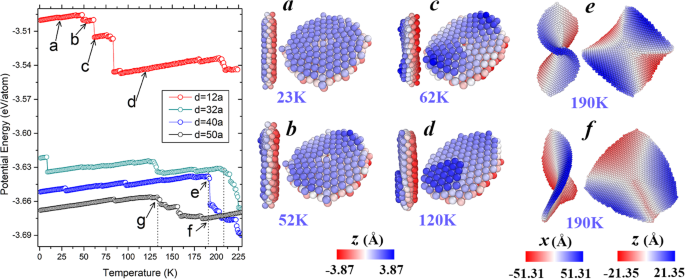
Painel esquerdo:Evolução da temperatura das energias potenciais de nanoplacas bcc Fe (001) com diâmetros diferentes. Painel direito:instantâneos da nanoplaca com d =12 a em a 23 K, b 52 K, c 62 K e d 120 K; Instantâneos da nanoplaca com e d =40 a a 190 K e (f) d =50 a a 190 K

Além do efeito do diâmetro, nanoplacas com diferentes espessuras também são consideradas. A energia potencial da nanoplaca ( d =32 a ) com camadas diferentes são mostrados na Fig. 6. Observe que a nanoplaca de 3 camadas atômicas acima mencionada também é mostrada para comparação. Como visto a partir da evolução das energias potenciais, verifica-se que as nanoplacas com 1 ou 2 camadas atômicas experimentam obviamente mais estágios em comparação com aquela com 3 camadas. Na verdade, eles colapsam em formas irregulares em temperaturas muito mais baixas. Em contraste, a estrutura original da nanoplaca com 4 camadas é bem mantida até 97 K (cf. Fig. 6a). No entanto, a 98 K, seus planos tipo disco (001) se transformam em planos elípticos (110) com maior estabilidade (cf. Fig. 1), o que é acompanhado por uma diminuição abrupta na energia potencial. Esta nanoplaca gerada de 4 camadas (110) retém sua configuração até que ocorra a fusão. Esses resultados mostram que nanoplacas mais espessas geralmente apresentam melhor estabilidade, e o formato de sela só existe em espessuras relativamente pequenas. Para obter mais informações sobre a generalidade dos padrões de evolução, também modelamos várias outras nanoplacas metálicas bcc (incluindo W, Nb, Mo e Cr) com diâmetros de 32 a , que consistem em três camadas de (001) átomos orientados inicialmente. A Figura 7 ilustra as energias potenciais dependentes da temperatura dessas nanoplacas e os instantâneos atomísticos associados a temperaturas representativas. Após o relaxamento a 1 K, todos os planos originalmente uniformes (001) reconstroem e formam (110) facetas com diferentes orientações. Em temperaturas mais baixas, a forma de sela, como um estado metaestável universal, aparece em todas as nanoplacas, semelhante ao caso da nanoplaca de Fe. Com o avanço do aquecimento, a transformação em partícula irregular ocorre em diferentes temperaturas, onde as energias potenciais diminuem drasticamente. Comparativamente, o estágio de forma de sela para nanoplaca W dura na mais ampla faixa de temperatura (até 582 K), o que é atribuído à sua extraordinária estabilidade estrutural (inicial E _p =- 7,94 eV / átomo). Em contraste, a nanoplaca de Cr menos estável mantém sua forma de sela apenas até 62 K, após o qual os solavancos e flambagem aparecem sucessivamente (cf. as fotos tiradas a 61 e 250 K na Fig. 7). Quanto às outras duas nanoplacas, Nb tende a restaurar a superfície plana original (cf. o instantâneo de 135 K na Fig. 7), e Mo apresenta curvatura significativa (cf. o instantâneo de 150 K) antes de seu colapso final. Essas duas situações se assemelham aproximadamente às nanoplacas de Fe moduladas (110) e (001). Os resultados acima mostram que os estados metaestáveis observados nas nanoplacas de Fe também existem em outras nanoplacas metálicas bcc. Configurações com estabilidade estrutural diferente seguem padrões de evolução diferentes. Além disso, nota-se que na maioria de nossas simulações, as nanoplacas se transformam em partículas compactas mesmo abaixo da temperatura ambiente, o que é resultado de seus pequenos tamanhos. Ainda assim, os mecanismos de evolução identificados são de significado geral. Os resultados da estabilidade relativa dessas nanoplacas entre diferentes orientações, tamanhos e elementos planos podem ser extrapolados para sistemas maiores. A descrição dos mecanismos de transformação de forma pode servir como uma referência para a obtenção de morfologias desejadas através do controle de orientação cristalina ou liga [31, 32].

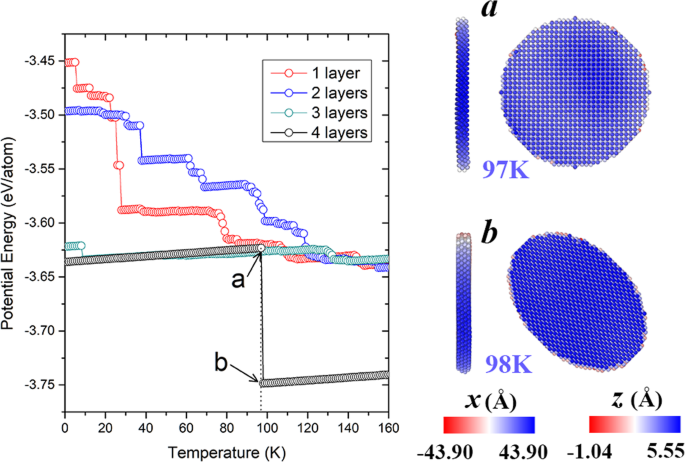
Painel esquerdo:Evolução da temperatura das energias potenciais de nanoplacas de Fe (001) com diferentes números de camadas. Painel direito:instantâneos da nanoplaca com 4 camadas respectivamente em a 97 K e b 98 K

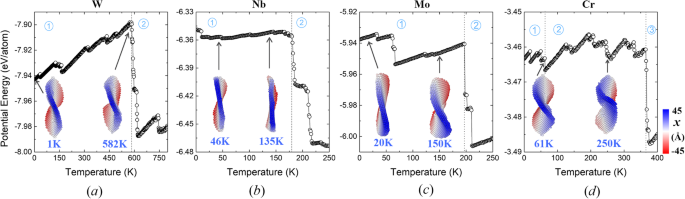
Evoluções de temperatura de energias potenciais de a W, b Nb, c Mo e d Nanoplacas de Cr, respectivamente. Instantâneos dos estados representativos são mostrados como inserções

Conclusões

Em resumo, a evolução da forma de nanoplacas de Fe bcc com superfícies de baixo índice foi investigada por simulações de MD. A discrepância na estabilidade estrutural leva a diversos padrões nas transformações morfológicas. (110) a nanoplaca é a mais estável e mantém sua configuração inicial até a temperatura máxima. Em contraste, as nanoplacas (111) e (001) não são capazes de existir com firmeza, ambas tendem a colapsar em partículas irregulares, mesmo abaixo da temperatura ambiente. No entanto, antes deste colapso final, a superfície da nanoplaca (001) se converte em (110) facetas com diferentes orientações e, entretanto, forma uma forma de sela, que se mantém em uma faixa de temperatura relativamente ampla. Esse processo de transformação é impulsionado pela tensão de cisalhamento, cuja distribuição está intimamente associada ao arranjo facetário. Flexão e empenamento adicionais durante o aquecimento subsequente correspondem à liberação de tensão. Além disso, foram realizadas simulações nas nanoplacas moduladas (110), nanoplacas (001) com diferentes diâmetros e espessuras e outras nanoplacas metálicas bcc (001). Os resultados mostram que a evolução da forma pode ser ajustada pelas orientações das facetas, tamanhos das placas e componentes. Este estudo divulga o mecanismo de evolução da forma em nível atômico de nanoplacas metálicas bcc e, assim, fornece uma base teórica sobre o controle da morfologia em sínteses de nanomateriais metálicos.

Disponibilidade de dados e materiais

Todos os dados gerados ou analisados durante este estudo estão incluídos neste artigo publicado.

Abreviações

a:: Estrutura constante
bcc:: Cúbico-centrado no corpo
d:: diâmetro
EAM:: Método de átomo incorporado
E _p :: Energia potencial
MD:: Dinâmica Molecular
R ² :: Coeficiente de determinação
TEM:: Microscopia eletrônica de transmissão

Estudo dos primeiros princípios de penta-siligrafeno como material de ânodo de alto desempenho para baterias de íons de lítio Caracterizações espectroscópicas Raman de nanoestruturas unidimensionais de InP / InAs / InP autocatalisadas em substrato InP (111) B usando um método de inclinação de substrato simples

Nanomateriais

Materiais Poliméricos

biológico

Corante

Especiarias