home Tecnologia de manufatura Equipamentos de Fabricação
Manufaturação industrial
Internet das coisas industrial | Materiais industriais | Manutenção e reparo de equipamentos | Programação industrial |
home  MfgRobots >> Manufaturação industrial >  >> Industrial materials >> Nanomateriais

Pseudomagnetoresistência de vale eletricamente controlada em grafeno com distorção de rede de Kekulé em forma de Y

Resumo


Propomos um novo método para regular a pseudomagnetoresistência de vale em transistores de efeito de campo de vale à base de grafeno balístico, levando em consideração a distorção da rede de Kekulé em forma de Y e a barreira elétrica. O dispositivo envolve injeção de vale e detecção de vale por fonte e dreno de tensão ferromagnética. A manipulação do vale no canal é obtida por meio da distorção da rede de Kekulé em forma de Y e da barreira elétrica. O mecanismo central desses dispositivos reside na distorção da rede de Kekulé em forma de Y no grafeno pode induzir uma precessão de vale, controlando assim a orientação de vale dos elétrons do canal e, portanto, a corrente coletada no dreno. Descobrimos que a tensão de polarização externa de sintonia faz a pseudomagnetoresistência de vale oscilar entre valores positivos e negativos e uma pseudomagnetoresistência de vale de tunelamento colossal de mais de 30.000% pode ser alcançada. Nossos resultados sugerem que a sinergia de Valleytronic e lógica digital pode fornecer novos paradigmas para processamento de informação baseado em Valleytronic e computação reversível.

Introdução


O grafeno, sendo uma folha bidimensional de átomos de carbono, que tem excelente mobilidade de portadores e oferece o canal mais fino possível para utilização no projeto de transistores de efeito de campo semicondutores de óxido metálico [1]. Semenov propôs um transistor de efeito de campo de spin utilizando uma camada de grafeno como canal [2], que envolve injeção de spin e detecção de spin por fonte ferromagnética e dreno, e a manipulação de spin no canal é obtida por meio do controle elétrico da troca de elétrons. interação com uma porta ferromagnética. Além disso, a interação spin-órbita de Rashba é outra ferramenta promissora para o controle de spin no grafeno [3]. A interação spin-órbita de Rashba pode induzir uma precessão do spin, controlando assim a orientação do spin dos elétrons do canal. Os transistores de efeito de campo de spin também inspiraram muitas idéias importantes de pesquisa, como a magnetorresistência gigante e a magnetorresistência de túnel [3, 4]. A magnetorresistência gigante e a magnetorresistência de túnel podem ser aplicadas em tecnologias de armazenamento digital e sensores magnéticos.

Por outro lado, os elétrons de Dirac no grafeno possuem grau de liberdade extra vale além da carga convencional e contrapartes de spin. Devido à grande diferença de momento entre os dois vales e a supressão do espalhamento intervalley em amostras de grafeno limpo [5-7], acredita-se que o grau de liberdade do vale exerce o mesmo efeito que o spin do elétron no transporte e manipulação de informações, que leva a uma nova disciplina que surge como Valleytronics. No análogo do transistor de efeito de campo de spin, o transistor de efeito de campo de vale também é teoricamente proposto no grafeno [8], que consiste em um canal quântico de uma dimensão de grafeno com lacuna imprensado entre duas nanofitas de grafeno poltrona (fonte e dreno); então, o campo elétrico da porta lateral é aplicado ao canal e modula a polarização de vale dos portadores devido à interação vale-órbita, controlando assim a quantidade de corrente coletada no dreno. No entanto, devido ao fato de que o acoplamento de vale no grafeno não se tornou uma realidade física por um longo tempo, existem poucos estudos adicionais baseados nos transistores de efeito de campo do vale do grafeno e estudos relacionados. Experimentos recentes de Gutierrez et al. [9] revelaram uma textura de ligação Kekulé (Kek-Y) em forma de Y incomum na rede do favo de mel em uma superrede de cobre-grafeno, onde um dos seis átomos de carbono em cada célula unitária da superrede não tem átomos de cobre abaixo dele e adquire um menor vínculo com o vizinho mais próximo. Além disso, Gamayun mostrou que a textura de ligação Kek-Y oferece um caminho para uma precessão de vale controlada por momentum [10]. Beenakker et al. [11] mostraram que o sistema Kek pode trazer um efeito de vale invertido através do reflexo do tipo Andreev. Rencently Wang et al. [12] descobriram que a modulação do comprimento da ligação C-C da rede de Kekulé que mantém a simetria de inversão do sistema pode ser usada para manipular o grau de liberdade do vale de uma forma semelhante ao spin de precessão do campo de troca. Isso torna possível projetar um novo tipo de transistor de efeito de campo de vale em grafeno. Além disso, não há nenhum relato sobre os efeitos combinados da distorção da rede Kek-Y na pseudomagnetoresistência de vale no grafeno. A pseudomagnetoresistência Valley [13, 14] é análoga à magnetorresistência na junção do túnel magnético [15] onde a magnitude da corrente de spin depende da orientação magnética dos eletrodos [4].

Métodos


Neste trabalho, propomos um novo tipo de transistores de efeito de campo de vale (VFETs) para elétrons baseados em grafeno. O projeto do dispositivo assume uma fonte / dreno de deformação ferromagnética (FM-S) para injeção / detecção de vale polarizado, que se assemelha a um transistor de spin convencional (ver Fig. 1a). A rotação do vale no canal de grafeno depende da superrede de grafeno Kek-Y [10-12], que pode ser alcançada por uma superrede de grafeno desenvolvida epitaxialmente em Cu (111), com os átomos de cobre em registro com os átomos de carbono [9]. No entanto, faltam átomos de cobre em alguns átomos de carbono, resultando em algumas lacunas periódicas de átomos de cobre que aparecem abaixo do grafeno. Essa vacância do átomo do substrato leva à contração de três ligações vizinhas. Aqui, usamos δ t para representar a modificação de energia para o salto do elétron correspondente a essas três ligações. Assumimos que o grafeno ferromagnético é feito da mesma faixa de metal FM. As duas magnetizações da fonte e do dreno são direcionadas ao longo da direção da corrente (o x eixo), que pode estar no alinhamento paralelo (P) ou antiparalelo (AP), com a ajuda de um campo magnético externo no plano. No medidor de Landau, o potencial do vetor magnético decorrente do campo periférico tem a forma [16, 17] \ (A (r) =A_ {y} (x) \ overrightarrow {y} \) com A y ( x ) = A y [ Θ (- x ) ± Θ ( x - L )], onde o sinal de mais (menos) corresponde à configuração P (AP) de magnetizações, Θ ( x ) é a função de etapa de Heaviside. Por outro lado, assumimos que as mesmas deformações são aplicadas na fonte e no dreno dos VFETs, o que pode ser induzido por uma tensão no substrato do grafeno [18]. A deformação elástica pode ser tratada como uma perturbação das amplitudes de salto e atua como um potencial medidor A S ( r ) A tensão é definida ao longo do x direção, neste caso, A S ( r ) uniforme ao longo do y eixo [16]. Para definição, tomamos um perfil suave típico de seu y componente como A Sy ( x ) = A S [ Θ (- x ) + Θ ( x - L )], onde A S é a amplitude. Além disso, uma barreira elétrica também é aplicada na região da rede Kek-Y, que pode ser ajustada por tensão de polarização externa.

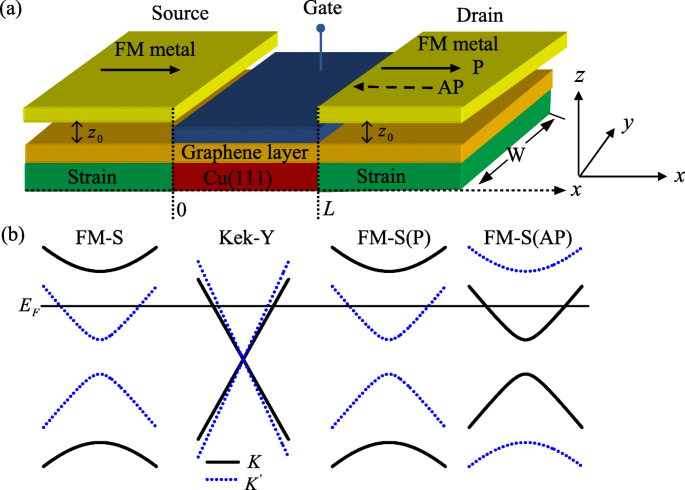
a Ilustração esquemática do VFET utilizando um canal de grafeno com distorção de rede Kek-Y e uma polarização de porta, que controla a orientação de vale dos elétrons do canal. A fonte e o dreno são o grafeno FM-S, que injeta e detecta elétrons em uma polarização específica. Onde z 0 é a distância entre a camada de grafeno e a faixa FM. L é o comprimento do canal, W é a largura da amostra de grafeno no y direção e W ≫ L . b Estrutura da banda perto dos pontos de Dirac. A linha horizontal denota a energia Fermi (cor online)

A propagação de quasipartículas de excitação de baixa energia nos VFETs com superredes de grafeno Kek-Y pode ser descrita por estes seguintes hamiltoniano de partícula única [10-12]
$$ \ begin {array} [c] {ll} H =&v_ {F} (\ mathbf {P} \ cdot \ sigma) + v _ {\ tau} (\ mathbf {P} \ cdot \ tau) \ Theta \ left (x \ right) \ Theta \ left (Lx \ right) + \\ &U \ sigma_ {0} \ tau_ {0} \ Theta \ left (x \ right) \ Theta \ left (Lx \ right) + A_ {M} (x) \ sigma_ {y} + \ tau_ {z} A_ {S} (x) \ sigma_ {y}. \ end {array} $$ (1)
Aqui, σ e τ são as matrizes de Pauli para a sub-rede e o vale, respectivamente. P =( p x , p y ) é o momento dos elétrons de Dirac sem massa, τ z =± 1 para K e \ (K ^ {^ {\ prime}} \) vales, v F =10 6 m / s é a velocidade dos elétrons de Dirac no grafeno puro, e v τ ≃ v F δ t / 3 t é o termo de modificação de velocidade do efeito de contração da ligação na rede Kek-Y [12], onde t é a energia de salto entre as cidades vizinhas mais próximas para o grafeno puro. U é a barreira de potencial sintonizável pela porta. A M ( x ) = e v F A y ( x ) [19]. Os valores próprios do hamiltoniano no grafeno com distorção da rede Kek-Y e barreira elétrica são dados por
$$ E _ {\ alpha, \ beta} =U + \ alpha (\ hbar v_ {F} + \ beta \ hbar v _ {\ tau}) \ sqrt {k_ {x \ beta} ^ {2} + k_ {y} ^ {2}}. $$ (2)
Aqui, α =+ 1 (−1) especifica a banda de condução (valência). β =± 1 denota as duas sub-bandas de vale-divisão das bandas de condução e valência. Devido à invariância translacional no y direção, o vetor de onda transversal k y é conservado. Os autoestados no grafeno com a distorção homogênea da rede Kek-Y são caracterizados por \ (\ Psi _ {\ beta} ^ {\ pm} (k_ {x \ beta}, k_ {y}) =\ frac {1} { N _ {\ beta}} \ left (1, P _ {\ beta} ^ {\ pm}, Q _ {\ beta} ^ {\ pm}, R _ {\ beta} ^ {\ pm} \ right) ^ {T} \), onde N β é a constante de normalização \ (N _ {\ beta} =\ left (1 + P _ {\ beta} ^ {2} + Q _ {\ beta} ^ {2} + R _ {\ beta} ^ {2} \ right) ^ {\ frac {1} {2}} \) e \ (P _ {\ beta} ^ {\ pm}, Q _ {\ beta} ^ {\ pm} \), e \ (R _ {\ beta} ^ {\ pm} \) são funções definidas da seguinte forma:
$$ \ begin {array} [c] {cc} P _ {\ beta} ^ {\ pm} =&\ frac {(EU) ^ {2} + \ left (\ hbar ^ {2} v_ {F} ^ {2} - \ hbar ^ {2} v _ {\ tau} ^ {2} \ right) \ left (k_ {x \ beta} ^ {2} + k_ {y} ^ {2} \ right)} {2 (EU) \ hbar v_ {F} (\ pm k_ {x \ beta} - {ik} _ {y})}, \\ Q _ {\ beta} ^ {\ pm} =&\ frac {(EU) ^ {2} - \ left (\ hbar ^ {2} v_ {F} ^ {2} - \ hbar ^ {2} v _ {\ tau} ^ {2} \ right) \ left (k_ {x \ beta} ^ {2} + k_ {y} ^ {2} \ right)} {2 (EU) \ hbar v _ {\ tau} (\ pm k_ {x \ beta} - {ik} _ {y})}, \\ R _ {\ beta} ^ {\ pm} =&\ frac {(EU) ^ {2} - \ left (\ hbar ^ {2} v_ {F} ^ {2} + \ hbar ^ {2} v _ {\ tau} ^ {2} \ right) \ left (k_ {x \ beta} ^ {2} + k_ {y} ^ {2} \ right)} {2 \ hbar ^ {2} v_ {F} v _ {\ tau} (\ pm k_ {x \ beta} - {ik} _ {y}) ^ {2}}. \ end {array} $$ (3)
A probabilidade de transmissão de \ (K ^ {^ {\ prime}} \) vale para \ (K (K ^ {^ {\ prime}}) \) vale \ (T_ {K ^ {^ {\ prime}}, K (K ^ {^ {\ prime}})} \) pode ser calculado usando a técnica da matriz de transferência [20]. De acordo com a fórmula de Laudauer-Btittiker, a condutância dependente do vale é dada por [21]:
$$ G_ {K ^ {^ {\ prime}}, K (K ^ {^ {\ prime}})} =G_ {0} {\ int _ {- \ frac {\ pi} {2}} ^ {\ frac {\ pi} {2}}} T_ {K ^ {^ {\ prime}}, K (K ^ {^ {\ prime}})} \ cos (\ phi_ {0}) d \ phi_ {0} . $$ (4)
Aqui \ (G_ {0} =2e ^ {2} W / \ left (v_ {F} \ pi ^ {2} \ hbar ^ {2} \ right) \ left \ vert E \ right \ vert \), W é a largura da amostra de grafeno no y direção e ϕ 0 é o ângulo de incidência em relação ao x direção.

Antes de prosseguir com os cálculos, discutimos a estrutura da banda com k y =0, conforme mostrado na Fig. 1b. Na região da fonte FM-S, a banda de energia do grafeno é escrita como \ (E =\ alpha \ sqrt {(\ hbar v_ {F} k_ {x}) ^ {2} + (A_ {M} + \ tau _ {z} A_ {S}) ^ {2}} \). Pode-se descobrir que o vale degenerado é elevador e diferentes lacunas são induzidas no K e \ (K ^ {^ {\ prime}} \) pontos porque o potencial total do vetor A M + A S agindo em K elétrons é maior do que o potencial total do vetor | A M - A S | agindo por \ (K ^ {^ {\ prime}} \) elétrons [19]. Isso indica que apenas \ (K ^ {^ {\ prime}} \) elétrons podem passar pela região da fonte FM-S quando a energia incidente está localizada em | A M - A S | < E < A M + A S [22, 23]. Da mesma forma, na região de drenagem FM-S, a banda de energia do grafeno pode ser escrita como \ (E =\ alpha \ sqrt {(\ hbar v_ {F} k_ {x}) ^ {2} + (\ pm A_ { M} + \ tau _ {z} A_ {S}) ^ {2}} \), onde o sinal ± corresponde à configuração P e AP das magnetizações. Portanto, apenas \ (K ^ {^ {\ prime}} \) elétrons são detectados na estrutura P e apenas K elétrons são detectados na estrutura AP quando a energia de Fermi se localiza na faixa de [| A M - A S |, A M + A S ] No canal do grafeno, o vale degenerado também é elevador, mas há uma diferença importante. Em contraste com o caso principal, onde as fases de K e \ (K ^ {^ {\ prime}} \) componentes evoluem com o mesmo vetor de onda [ou seja, \ (k =E / \ hbar v_ {F} \)], agora, eles evoluem separadamente com diferentes vetores de onda ( \ (k _ {+} =(EU) / (\ hbar v_ {F} + \ hbar v _ {\ tau}) \) e \ (k _ {-} =(EU) / (\ hbar v_ {F} - \ hbar v _ {\ tau}) \)) devido às superredes de grafeno Kek-Y que misturam o vale (ver Eq. 2). Isso leva à precessão do vale dos elétrons do canal no espaço do vale [12]. A precessão de vale no grafeno é a base para o transistor de efeito de campo de vale [8]. E a precessão de vale também pode ser caracterizada por uma pseudomagnetoresistência de vale (VPMR) nas junções FM-S / Kek-Y / FM-S, análoga à magnetorresistência em junções de tunelamento quântico baseadas em grafeno com a interação spin-órbita [4] , que é definido como \ (VPMR =\ frac {G_ {P} -G_ {AP}} {G_ {P}} \), onde G P e G AP representam a condutância nas configurações P e AP, respectivamente, e \ (G_ {P} =G_ {K ^ {^ {\ prime}}, K ^ {^ {\ prime}}}, G_ {AP} =G_ {K ^ {^ {\ prime}}, K} \). A magnitude da corrente do vale depende da orientação magnética da fonte e do dreno em nosso dispositivo considerado.

Resultados numéricos e discussões


A seguir, apresentamos os resultados numéricos para a junção FM-S / Kek-Y / FM-S no grafeno. Ao longo do artigo, definimos o comprimento do canal L =207 nm, e restringe a energia de Fermi 20 meV < E <140meV, presumiu que satisfazia | A M - A S | < E < A M + A S . As Figuras 2a eb mostram os resultados calculados de condutância de tunelamento e VPMR em função de v t com energia Fermi E =80meV e barreira de potencial retângulo U =−10meV. Podemos descobrir que G P e G AP têm os mesmos períodos de oscilação, mas as fases inversas. Portanto, o VPMR oscila com aumento de v t e o valor negativo VPMR pode aparecer. Esses fenômenos são semelhantes ao caso da magnetorresistência em junções de tunelamento quântico balístico baseadas em grafeno com a interação spin-órbita [4]. Os caracteres de oscilação da condutância de G P e G AP pode ser explicado pela diferença de fase entre os dois componentes do vale. Quando o ângulo de incidência ϕ 0 =0, a mudança de fase é dada por:\ (\ Delta \ theta =(k_ {x +} - k_ {x -}) L =- \ frac {2 (EU) v _ {\ tau}} {\ hbar (v_ {F} ^ {2} -v _ {\ tau} ^ {2})} L \). Δ θ determina a orientação da polarização de vale antes que o elétron entre no dreno, em relação ao estado de dreno [8]. Para Δ θ =± 2 n π , n =1,2,3 ⋯, as duas polarizações estão alinhadas, levando à condutância G P máximo e VPMR um valor positivo alto (como visto em v τ =0,022, 0,033). Por outro lado, para Δ θ =± (2 n +1) π , n =0,1,2 ⋯, eles são ortogonais entre si, levando à condutância G AP mínimo e VPMR negativo (como visto em v τ =0,0167, 0,027, 0,038).

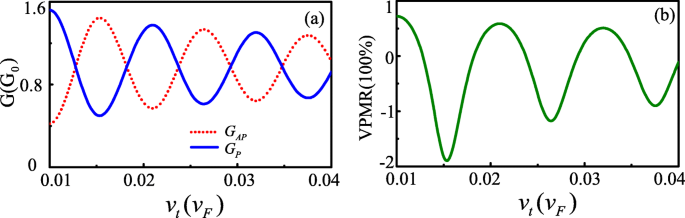
Condutância G P , A P e VPMR versus v t em L =207 nm, E =80meV e U =−10meV (cor online)

A condutância e o VPMR não são apenas funções de oscilação da modificação da energia de salto, mas também oscilam com a energia de Fermi e o potencial de barreira efetivo desde Δ θ escalas também são lineares com a energia de Fermi e a barreira de potencial U . As Figuras 3a eb mostram a condutância em função da energia de Fermi e do potencial de barreira efetivo, respectivamente. O VPMR correspondente é dado nas Fig. 3c e d. Todos eles mostram características de oscilação variando com E e U valor, mesmo quando o potencial de barreira efetiva U é maior que a energia de Fermi E . A origem física para tal fenômeno está relacionada ao tunelamento de Klein [12]. Embora existam fenômenos de oscilação semelhantes de condutância e VPMR para aumento de E e U , algumas diferenças também podem ser encontradas. Como E aumenta, a diferença entre G P e G AP a condutância torna-se cada vez menor, o que faz com que a amplitude de oscilação do VPMR diminua com o aumento da energia de Fermi. Enquanto estiver sob a condição Δ θ =± n π está satisfeito, a diferença entre G P e G AP é maior com o aumento de U , especialmente em algum local, o G P e G AP a condutância apresenta características de comutação. Os personagens são mais desejáveis ​​para a aplicação do VPMR. Surpreendentemente, o valor máximo observado de VPMR é superior a 30.000% em pequeno E . Este valor excede em muito o MR de ~ 175 % nas junções de tunelamento quântico balístico baseadas em grafeno com a interação spin-órbita [4] e a pseudomagnetoresistência de ~ 100 % em grafeno de duas camadas controlado por portas externas [24], que é ainda maior do que o VPMR de ~ 10.000 % em um sistema de cones de Dirac mesclado [13].

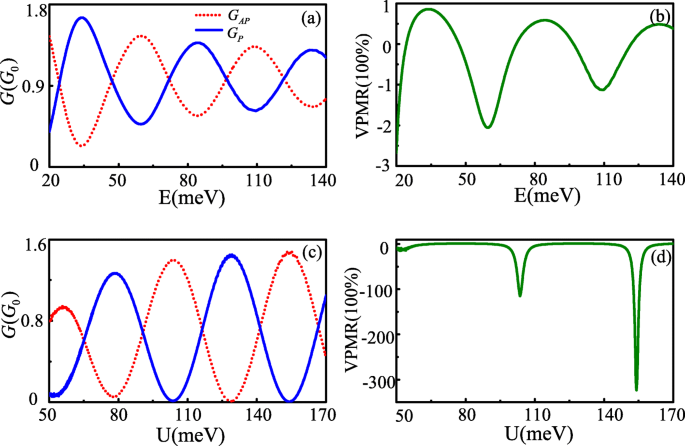
Condutância G P , A P ( a , c ) e VPMR ( b , d ) como funções da energia de Fermi e da barreira elétrica em L =207 nm, v t =0,02 v f . os outros parâmetros são U =−10meV para a e c , E =80meV para b e d (cor online)

Conclusões


Em conclusão, propusemos um tipo de transistores de efeito de campo de vale para elétrons à base de grafeno e estudamos a pseudomagnetoresistência de vale através dele. Mostramos que a característica de oscilação da pseudomagnetoresistência de vale não está apenas relacionada com a modificação da energia de salto e energia de Fermi, mas também pode ser amplamente ajustada pelo potencial de barreira efetivo. A pseudomagnetoresistência de vale sintonizada por tensão de polarização externa beneficia o dispositivo transistor de efeito de campo de vale, e prevemos que os dispositivos quânticos de vale controlados elétricos aqui propostos podem desempenhar um papel em computadores quânticos e híbridos quânticos clássicos.

Pesquisas adicionais podem envolver a tensão diferente (uniaxial vs. biaxial) sintonizável do espalhamento de vale de elétrons e transporte em nossos transistores de efeito de campo de vale baseados em grafeno, uma vez que a mancha é útil para controlar o grau de espalhamento intervalley em padrões de Kekulé [25] . Em seguida, outros materiais bidimensionais (MoS 2 , WS 2 , WSe 2 , etc.) análogos no grafeno também podem fornecer uma plataforma interessante para outros transistores de efeito de campo de vale baseados em material bidimensional com distorção de rede Kekulé em forma de Y.

Disponibilidade de dados e materiais


Os conjuntos de dados que suportam as conclusões deste artigo estão incluídos no artigo.

Abreviações

AP:

Antiparalelo
FM-S:

Cepa ferromagnética
Kek-Y:

Kekulé em forma de Y
P:

Paralelo
VFETs:

Transistores de efeito de campo Valley
VPMR:

Valley pseudomagnetoresistência

Nanomateriais

  • Metal
  • Resina
  • fibra
  • Material compósito
  • Nanomateriais
  • Materiais Poliméricos
  • biológico
  • Corante
  • Especiarias
    1. Lattice:MachX03D FPGA aumenta a segurança com recursos de raiz de confiança de hardware
    2. Grafeno Coloca Nanomateriais em Seu Lugar
    3. Grafeno em alto-falantes e fones de ouvido
    4. Nanofibra de grafeno
    5. RGO e redes de grafeno tridimensionais TIMs co-modificados com alto desempenho
    6. Avaliação de estruturas de grafeno / WO3 e grafeno / CeO x como eletrodos para aplicações de supercapacitor
    7. Aerogel de Grafeno / Polianilina com Superelasticidade e Alta Capacitância como Eletrodo de Supercapacitor Altamente Tolerante à Compressão
    8. Síntese fácil e ecológica de nanofios de Co3O4 e sua aplicação promissora com grafeno em baterias de íon-lítio
    9. Nanocompósitos à base de óxido de grafeno decorados com nanopartículas de prata como agente antibacteriano
    10. Preparação de polietileno de peso molecular ultra-alto / nanocompósito de grafeno polimerização in situ via estrutura esférica e sanduíche de grafeno / suporte Sio2