Estrutura Eletrônica Dependente de Spin e Valley em Siliceno sob Potenciais Periódicos

Resumo

Nós estudamos a banda de energia dependente de spin e vale e a propriedade de transporte do siliceno sob um potencial periódico, onde as degenerescências de spin e vale são elevadas. Verificou-se que o ponto de Dirac, minibanda, gap, velocidade anisotrópica e condutância dependem fortemente dos índices de spin e vale. Os pontos de Dirac extras aparecem à medida que o potencial de voltagem aumenta, os valores críticos dos quais são diferentes para elétrons com diferentes spins e vales. Curiosamente, a velocidade é bastante suprimida devido ao campo elétrico e ao campo de troca, além do grafeno sem intervalos. É possível obter um excelente efeito de colimação para um spin específico próximo a um vale específico. A estrutura de banda dependente de spin e vale pode ser usada para ajustar o transporte, e transmissões perfeitas são observadas em pontos de Dirac. Portanto, uma notável polarização de spin e vale é alcançada, a qual pode ser comutada efetivamente pelos parâmetros estruturais. É importante notar que as polarizações de spin e vale são bastante aumentadas pela desordem do potencial periódico.

Histórico

Materiais bidimensionais (2D) Dirac com estruturas de rede hexagonal estão sendo explorados extensivamente desde a descoberta do grafeno, como siliceno [1, 2], dichalcogenetos de metais de transição [3, 4] e fosforeno [5]. Embora o grafeno tenha muitas propriedades particulares, sua aplicação é limitada pelo gap zero e pela interação spin-órbita fraca (SOI). Recentemente, um análogo do grafeno ao silício, o siliceno, foi fabricado via crescimento epitaxial [6–10], e sua estabilidade foi prevista por estudos teóricos [11, 12]. Grafeno e siliceno têm estruturas de banda semelhantes em torno de K e K ^′ vales, e os espectros de baixa energia de ambos são descritos pela equação relativística de Dirac [13]. Ao contrário do grafeno, o siliceno tem um forte SOI intrínseco e uma estrutura curvada. O forte SOI poderia abrir uma lacuna nos pontos de Dirac [13, 14] e levar a um acoplamento entre os graus de liberdade de spin e vale. A estrutura curvada nos permite controlar o gap por um campo elétrico externo perpendicular à folha de siliceno [14-16]. Além disso, o siliceno tem a vantagem de ser mais compatível com a tecnologia eletrônica baseada em silício existente. Essas características tornam o siliceno um excelente material para a nanoeletrônica de última geração. Em particular, um transistor de efeito de campo de siliceno em temperatura ambiente foi fabricado com sucesso por um processo de fabricação de transferência de crescimento em experimento [17].

A descoberta de materiais 2D Dirac oferece novas oportunidades para explorar o controle quântico do vale. Os dois vales inequivalentes K e K ^′ na primeira zona de Brillouin poderia ser considerada como um grau adicional de liberdade além de carga e spin para informação quântica e computação quântica [18-20]. Por exemplo, o grau de liberdade de vale pode ser incorporado para expandir um qubit de spin de elétron para um qubit de vale de spin [18]. Portanto, valleytronics que visa gerar, detectar e manipular o pseudospin de vale tem atraído considerável interesse. No grafeno, vários esquemas para atingir uma polarização de vale foram propostos utilizando modos de borda únicos [21, 22], efeito de deformação trigonal [23], defeitos de linha topológica [24, 25], deformação [26, 27] e portas eletrostáticas [28]. Comparado ao grafeno, o siliceno tem vantagem significativa no estudo do vale pseudospin. Verificou-se que siliceno exibe uma rica variedade de fases topológicas e números de Chern sob a modulação de diferentes campos externos [13, 16, 29, 30]. Na presença de campo elétrico E _z e campo de câmbio h , Ezawa explorou o diagrama de fases no E _z - h plano que é caracterizado pelos índices de spin e vale [16]. Além disso, considerando o Rashba SOI, um estado Hall anômalo quântico polarizado em vale é previsto no siliceno devido à transição de fase topológica [31]. Com base na transição de estado, um filtro de spin baseado em siliceno com quase 100% de polarização de spin é proposto, o qual é robusto contra desordem fraca [32]. Yokoyama estudou o transporte balístico através de uma junção ferromagnética (FM) de siliceno e demonstrou um spin e uma corrente polarizada de vale controláveis [33]. Em dichalcogenetos de metais de transição com uma simetria de inversão quebrada, a divisão de spin das bandas de valência decorrentes do SOI intrínseco é oposta nos dois vales devido a uma simetria de reversão no tempo [3, 34, 35]. A simetria de inversão quebrada pode resultar em uma regra de seleção óptica dependente do vale, que pode ser usada para excitar seletivamente portadores no K ou K ^′ vale via luz polarizada circularmente à direita ou à esquerda, respectivamente [3, 34]. No experimento, o sinal de polarização de vale foi sondado por medidas ópticas [36, 37] e de transporte [38, 39]. Um efeito Hall de vale gigante não local foi observado no grafeno de duas camadas submetido a um campo elétrico de porta de quebra de simetria, e o sinal não local persiste até a temperatura ambiente [38]. Uma revisão recente da Valleytronics em materiais 2D Dirac é fornecida na Ref. [40].

Superlattice é um método eficaz de engenharia da estrutura eletrônica em semicondutores e materiais 2D [41]. Padrões de superrede com nanoescala podem surgir naturalmente em experimentos quando grafeno ou siliceno são colocados em cima de substratos metálicos [42, 43]. Uma superrede no grafeno pode levar à renormalização da velocidade de Fermi anisotrópica [44] e geração de novos pontos de Dirac no espectro [45-47] devido à natureza quiral, que foi experimentalmente observada [43, 48, 49]. Superredes em siliceno com campo elétrico E _z e campo de câmbio h , ambas as degenerescências de spin e vale são eliminadas. É confirmado que a estrutura da minibanda e minigaps causados pelas superredes dependem dos índices de spin e vale [50]. Além disso, as polarizações de spin e vale podem ser aumentadas pelas superredes de siliceno [51]. Assim como o grafeno, muitas novas estruturas eletrônicas são esperadas em superredes de siliceno. No entanto, os trabalhos em superredes de siliceno são muito poucos [50, 51]. Neste artigo, discutimos em detalhes um aspecto complementar, a saber, a estrutura de banda dependente de spin e vale e a propriedade de transporte do siliceno. Descobrimos que os índices de spin e vale têm impactos diferentes nos pontos de Dirac extras e na velocidade anisotrópica que podem ser ajustados pelos parâmetros estruturais. A velocidade é bastante suprimida devido ao campo elétrico e ao campo de troca. Consegue-se uma notável polarização de spin e vale, que pode ser bastante intensificada pelo distúrbio.

O artigo está organizado da seguinte forma. Na seção “Métodos”, apresentamos o formalismo teórico e a relação de dispersão. Os resultados numéricos sobre a estrutura de banda, transmissões polarizadas de spin e vale são mostrados na seção “Resultados e discussões”. Por fim, concluímos com um resumo na seção “Conclusões”.

Métodos

Na aproximação de partícula única, a estrutura eletrônica do siliceno na vizinhança dos pontos de Dirac obedece a um hamiltoniano de Dirac efetivo. O sistema em consideração é uma superrede unidimensional de siliceno formada por uma série de barreiras potenciais locais U , campos de câmbio h , e campo elétrico perpendicular E _z . U , h , e E _z estão presentes apenas nas regiões de barreira com largura de barreira d _b , enquanto U = h = E _z =0 nas regiões de poço com largura de poço d _w , como mostrado na Fig. 1. A superrede com um tipo Kronig-Penney varia apenas ao longo de x direção, e o comprimento de uma unidade é d = d _b + d _w . Modelo semelhante foi discutido nas Refs. [51, 52], que se concentra principalmente no transporte termoelétrico e eletrônico, em vez da estrutura de banda e efeito de desordem estudados neste trabalho. Experimentalmente, U pode ser produzido pelas portas metálicas e h pode ser produzido pelo efeito de proximidade magnética com isoladores FM EuO [33], que são depositados periodicamente no topo da camada de siliceno (ver Fig. 1). O campo elétrico E _z aplicado perpendicular ao siliceno pode induzir um potencial de sub-rede escalonado Δ _z = ℓ E _z , com 2 ℓ ≈0,46Å a separação vertical de A e B locais das duas sub-redes devido à estrutura deformada [16]. Portanto, os estados eletrônicos podem ser descritos pelo Hamiltoniano,
$$ \ begin {array} {@ {} rcl @ {}} H =\ hbar v_ {F} (k_ {x} \ tau_ {x} - \ eta k_ {y} \ tau_ {y}) + \ Delta_ {\ eta \ sigma} \ tau_ {z} + U _ {\ sigma}. \ end {array} $$ (1)

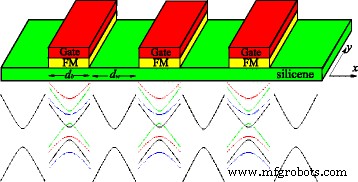
Acima:esquema das superredes de siliceno. Os isoladores FM, como EuO e EuS, no topo do siliceno induzem os campos de troca no siliceno, como proposto para o grafeno [53]. As portas metálicas no topo dos isoladores FM controlam o nível de Fermi localmente. Abaixo:esquemático do espectro de energia em siliceno com e sem campos externos

Δ _{η σ} = Δ _z - η σ λ _SO descreve a lacuna de banda para diferentes índices de spin e vale, que podem ser controlados pelo potencial escalonado Δ _z e o SOI λ _SO . U _σ = U - σ h é o potencial efetivo para diferentes índices de spin. η =± 1 denota o K e K ^′ vales. σ =± 1 denota estados de aumento e redução de rotação. v _F é a velocidade de Fermi. No siliceno, os efeitos intrínsecos e extrínsecos de Rashba são muito pequenos e podem ser negligenciados [15].

Devido à invariância translacional ao longo do y direção, o vetor de onda transversal k _y é conservado. A função de onda para vale η e gire σ em cada região tem a forma Ψ ( x , y ) = ψ ( x ) e ^iky _y com
$$ \ begin {array} {@ {} rcl @ {}} \ psi (x) =A \ left (\ begin {array} {cc} 1 \\ \ frac {\ hbar v_ {F} k _ {-} } {\ epsilon _ {\ eta \ sigma}} \ end {array} \ right) e ^ {i q _ {\ eta \ sigma} x} + B \ left (\ begin {array} {cc} 1 \\ \ frac {- \ hbar v_ {F} k _ {+}} {\ epsilon _ {\ eta \ sigma}} \ end {array} \ right) e ^ {- i q _ {\ eta \ sigma} x}. \ end {array} $$ (2)
Nas regiões de barreira, ε _{η σ} = ε _b =( E - U _σ ) + Δ _{η σ} e o x componente do vetor de onda \ (q _ {\ eta \ sigma} =q_ {b} =\ sqrt {(E - U _ {\ sigma}) ^ {2} - \ Delta ^ {2} _ {\ eta \ sigma} - (\ hbar v_ {F} k_ {y}) ^ {2}} / \ hbar v_ {F} \). Nas regiões do poço, ε _{η σ} = ε _w = E - η σ λ _SO e \ (q _ {\ eta \ sigma} =q_ {w} =\ sqrt {E ^ {2} - \ lambda _ {SO} ^ {2} - (\ hbar v_ {F} k_ {y}) ^ { 2}} / \ hbar v_ {F} \). k _± = q _{η σ} ± i η k _y . A probabilidade de transmissão T _{η σ} pode ser calculado usando a técnica da matriz de transferência. A condutância normalizada para um spin particular em um vale particular a temperatura zero é dada por
$$ \ begin {array} {@ {} rcl @ {}} G _ {\ eta \ sigma} (E) =\ frac {1} {2} \ int _ {- \ pi / 2} ^ {\ pi / 2 } T _ {\ eta \ sigma} (E, E \ sin \ theta) \ cos \ theta d \ theta, \ end {array} $$ (3)
onde θ é o ângulo de incidência em relação ao x direção. As condutâncias resolvidas por spin e vale são definidas como \ (G _ {\ uparrow (\ downarrow)} =\ left (G_ {K \ uparrow (\ downarrow)} + G_ {K ^ {\ prime} \ uparrow (\ downarrow) )} \ right) / 2 \) and \ (G_ {K (K ^ {\ prime})} =\ left (G_ {K (K ^ {\ prime}) \ uparrow} + G_ {K (K ^ { \ prime}) \ downarrow} \ right) / 2 \), respectivamente. Em seguida, introduzimos a polarização de spin P _s e polarização de vale P _v :
$$ \ begin {array} {@ {} rcl @ {}} P_ {s} =(G _ {\ uparrow} - G _ {\ downarrow}) / (G _ {\ uparrow} + G _ {\ downarrow}), \ end {array} $$ (4) $$ \ begin {array} {@ {} rcl @ {}} P_ {v} =(G_ {K} - G_ {K ^ {\ prime}}) / (G_ { K} + G_ {K ^ {\ prime}}). \ end {array} $$ (5)
Com base no teorema de Bloch e na condição de continuidade das funções de onda, a relação de dispersão E ( k _x ) para elétrons de spin-up e spin-down perto de K e K ^′ vales podem ser calculados,
$$ \ begin {alinhado} \ cos (k_ {x} d) &=\ cos (q_ {w} d_ {w}) \ cos (q_ {b} d_ {b}) \\ &\ quad- \ frac {(\ epsilon_ {b} q_ {w}) ^ {2} + (\ epsilon_ {w} q_ {b}) ^ {2} + (\ epsilon_ {b} \! - \! \ epsilon_ {w}) ^ {2} k ^ {2} _ {y}} {2 \ epsilon_ {w} \ epsilon_ {b} q_ {w} q_ {b}} \ sin (q_ {w} d_ {w}) \ sin ( q_ {b} d_ {b}), \ end {alinhado} $$ (6)
e k _x é o número da onda de Bloch. Para simplificar o cálculo, as unidades adimensionais são introduzidas:\ (E \ rightarrow E d / \ hbar v_ {F} \), \ (U \ rightarrow U d / \ hbar v_ {F} \), \ (\ lambda _ {SO} \ rightarrow \ lambda _ {SO} d / \ hbar v_ {F} \), \ (\ Delta _ {z} \ rightarrow \ Delta _ {z} d / \ hbar v_ {F} \) , \ (h \ rightarrow hd / \ hbar v_ {F} \), k _y → k _y d , k _x → k _x d , d _w → d _w / d e d _b → d _b / d . Observe que em Δ _z = λ _SO = h =0, Eq. (6) é reduzido ao encontrado para o grafeno sem intervalos em um potencial periódico, onde tanto o spin quanto o vale são degenerados [44-47]. Da Eq. (6), podemos ver que o campo de troca h sozinho poderia induzir a divisão do spin, enquanto o vale mantém a degeneração. No entanto, a degeneração do vale pode ser eliminada pelo campo elétrico E _z com a ajuda do SOI λ _SO . Assim, uma combinação do campo de troca e do campo elétrico poderia levantar as degenerescências de spin e vale [16, 31-33], como mostrado na Fig. 1. No sistema proposto, elétrons com spins diferentes perto de vales diferentes apresentariam várias bandas estruturas e recursos de transporte.

Resultados e discussões

Nesta seção, usaríamos as equações acima para calcular as estruturas de banda e as propriedades de transporte para diferentes índices de spin e vale em superredes de siliceno. As larguras das barreiras e poços são consideradas iguais no que segue. Os resultados para o caso com poço e largura de barreira desiguais ( d _b ≠ d _w ) são semelhantes aos do grafeno sem intervalos [47]. Alguns parâmetros são definidos como d _b = d _w =50 nm e λ _SO =3,9 meV em siliceno, salvo indicação em contrário. Devemos nos concentrar nas duas primeiras minibandas (as minibandas de valência e condução mais baixas) perto do nível de Fermi.

Estrutura de banda dependente de spin e vale

Primeiro, o efeito do potencial U em minibandas é representado na Fig. 2. A fim de discutir o caso com lacuna e o caso sem intervalos de bandas de energia simultaneamente, definimos Δ _z =7,8 meV =2 λ _SO . Na ausência de potencial ( U =0), o elétron de spin-up próximo a K vale ( K ↑ elétron) e elétron spin-down próximo a K ^′ vale ( K ^′ ↓ elétron) não têm intervalos (ver Fig. 2 (a1, a4)), enquanto o elétron de spin-down próximo a K vale ( K ↓ elétron) e elétron de spin-up próximo a K ^′ vale ( K ^′ ↑ elétron) têm uma grande lacuna (ver Fig. 2 (a2, a3)). As minibandas de elétrons de spin-up (ou spin-down) mudam para a faixa de energia negativa (ou positiva) de E =0 por h , devido ao potencial efetivo U _σ = U - σ h . As estruturas de banda de K ↑ (ou K ↓ ) elétron e K ^′ ↓ (ou K ^′ ↑ ) elétron presente simetria de espelho em relação a E =0, consistente com a Eq. (6). No entanto, esta simetria de espelho é destruída na presença de U . Observavelmente, como U aumenta, aparecem pontos Dirac extras, cujo número aumenta entretanto. Os pontos de Dirac extras podem ser demonstrados pela quiralidade das funções de onda em sua vizinhança [46]. As características dos pontos de Dirac no sistema siliceno dependem fortemente dos graus de liberdade de spin e vale, como mostrado na Fig. 2. Por exemplo, em U =135 meV na Fig. 2 (d1 – d4) para K ↑ , K ↓ , K ^′ ↑ e K ^′ ↓ elétrons, os números dos pontos de Dirac são 5, 6, 4 e 7, respectivamente. Para valores específicos de U , como U =40,66 meV para K ↓ elétron (ver Fig. 2 (b2)) e U =100,63 meV para K ^′ ↑ elétron (ver Fig. 2 (c3)), um novo ponto de Dirac pode ser gerado em k _y =0, e ele se dividirá em um par que se move em direções opostas para longe do k _y =0 ponto, mas sempre mantendo k _x =0, como U aumentos adicionais. Em conseqüência, as lacunas de banda para K ↓ e K ^′ ↑ os elétrons são fechados (ver Fig. 2 (b2, c3)), e o sistema com intervalo torna-se sem intervalos. Para encontrar o valor crítico de U , definimos d _b = d _w e k _x =0. Analogamente à regra do grafeno sem intervalos [47], levando em consideração o teorema da função implícita, pode-se concluir que os vetores de onda longitudinais nos novos pontos de Dirac satisfazem q _b = q _w quando
$$ \ begin {array} {@ {} rcl @ {}} E_ {0} =\ frac {(U - \ sigma h) ^ {2} - \ Delta_ {z} ^ {2} + 2 \ eta \ sigma \ Delta_ {z} \ lambda_ {SO}} {2 (U - \ sigma h)}. \ end {array} $$ (7)

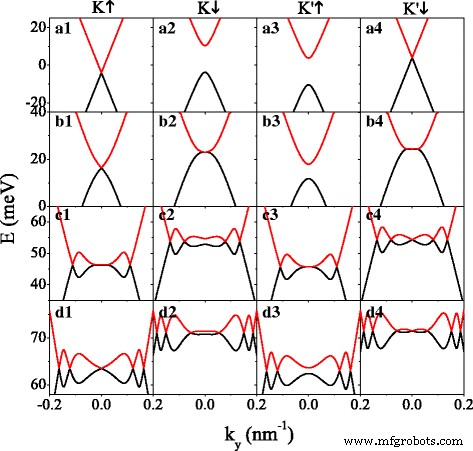
Espectro de energia versus k _y para vários valores diferentes de potencial U . (a1 – a4) U =0; (b1 – b4) U =40,66 meV; (c1-c4) U =100,63 meV; (d1 – d4) U =135,0 meV. Os valores dos parâmetros são h =8,0 meV, Δ _z =7,8 meV e k _x =0

Para K ↑ e K ^′ ↓ elétrons com η σ =1, quando Δ _z =2 λ _SO , Eq. (7) pode reduzir para
$$ \ begin {array} {@ {} rcl @ {}} E_ {0} =\ frac {U - \ sigma h} {2}. \ end {array} $$ (8)
Correspondentemente, a Eq. (6) se transforma em
$$ {} \ cos ^ {2} (q_ {w} d_ {w}) - \ frac {\ left (\ epsilon_ {b} ^ {2} + \ epsilon_ {w} ^ {2} \ right) q_ {w} ^ {2} + (\ epsilon_ {b} - \ epsilon_ {w}) ^ {2} k ^ {2} _ {y}} {2 \ epsilon_ {w} \ epsilon_ {b} q_ {w } ^ {2}} \ sin ^ {2} (q_ {w} d_ {w}) =1, $$ (9)
que é satisfeito quando \ (\ left (\ epsilon _ {b} ^ {2} + \ epsilon _ {w} ^ {2} \ right) q_ {w} ^ {2} + (\ epsilon _ {b} - \ epsilon _ {w}) ^ {2} k ^ {2} _ {y} =-2 \ epsilon _ {w} \ epsilon _ {b} q_ {w} ^ {2} \) ou q _w d =2 n π ( n é um número inteiro positivo). Com base na Eq. (8), temos ε _b =- ε _w , e assim a primeira igualdade é cumprida apenas se k _{y 0} =0 para K ↑ e K ^′ ↓ elétrons em Δ _z =2 λ _SO , correspondendo ao ponto Dirac original. As soluções de q _w d =2 n π tem o formulário
$$ \ begin {array} {@ {} rcl @ {}} k_ {y0} =\ pm \ frac {1} {d} \ sqrt {\ frac {\ left (E_ {0} ^ {2} - \ lambda_ {SO} ^ {2} \ right) d ^ {2}} {(\ hbar v_ {F}) ^ {2}} - (2n \ pi) ^ {2}}. \ end {array} $$ (10)
Quando \ (\ sqrt {E_ {0} ^ {2} - \ lambda _ {SO} ^ {2}} d / 2 \ pi \ hbar v_ {F} \ geq n \), k _{y 0} é real, e os novos pontos Dirac surgirão exatamente localizados em ( E ₀ , k _{y 0} ) Em valores baixos de U , k _{y 0} é imaginário e não há solução para n , o que significa nenhum ponto Dirac extra. Os pontos de Dirac aparecem apenas após um valor crítico de U , como U =40,66 meV para K ↓ elétrons na Fig. 2 (b2), correspondendo a n =1. De acordo com a Eq. (10), O número de pontos de Dirac N _D pode ser obtido. Quando Δ _z =2 λ _SO ,
$$ \ begin {array} {@ {} rcl @ {}} N_ {D} =2 \ left [\ frac {\ sqrt {E_ {0} ^ {2} - \ lambda_ {SO} ^ {2}} d} {2 \ pi \ hbar v_ {F}} \ right] + 1 \ end {array} $$ (11)
para K ↑ e K ^′ ↓ elétrons, enquanto
$$ \ begin {array} {@ {} rcl @ {}} N_ {D} =2 \ left [\ frac {\ sqrt {E_ {0} ^ {2} - \ lambda_ {SO} ^ {2}} d} {2 \ pi \ hbar v_ {F}} \ right] \ end {array} $$ (12)
para K ↓ e K ^′ ↑ elétrons, onde [...] denota uma parte inteira. Observe que no valor crítico de U , como U =40,66 meV e 100,63 meV, o número de pontos de Dirac é N _D =2 n -1 para K ↓ e K ^′ ↑ elétrons (ver Fig. 2 (b2, c3)).

As equações (7) e (10) manifestam que as posições e os números dos pontos de Dirac podem ser ajustados pelo campo elétrico E _z e campo de câmbio h . A Figura 3 exibe o número de pontos de Dirac N _D como uma função de U para diferentes valores de E _z e h . Quando Δ _z =7,8 meV na Fig. 3a, com aumento de U , N _D para K ↑ e K ^′ ↓ elétrons aumentam na forma de número ímpar, consistente com a Eq. (11). N _D para K ↓ e K ^′ ↑ elétrons aumentam na forma de número par, consistente com a Eq. (12), exceto para N _D no valor crítico. A comparação entre a Fig. 3a e b indica que como h aumenta, o valor crítico para o elétron de spin-down (ou spin-up) diminui (ou aumenta) gradualmente. Quando Δ _z =15 meV ≠ 2 λ _SO na Fig. 3c, N _D para todos os elétrons aumenta na forma de número par, exceto para N _D no valor crítico. Distintamente, os valores críticos de U são diferentes para elétrons com diferentes spins e vales. Os pontos de Dirac podem ser controlados por uma modulação conjunta dos parâmetros U , E _z e h .

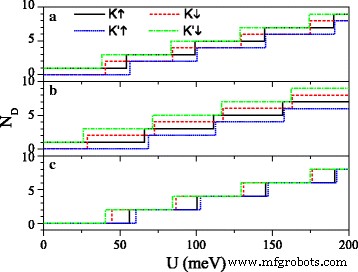
Número de pontos Dirac N _D versus potencial U . ( a ) h =8,0 meV e Δ _z =7,8 meV; ( b ) h =20,0 meV e Δ _z =7,8 meV; ( c ) h =8,0 meV e Δ _z =15.0 meV

O potencial U e largura da barreira d _b poderia ser usado para regular a lacuna de banda, conforme ilustrado na Fig. 4. As lacunas para K ↑ e K ^′ ↓ elétrons são pequenos, enquanto as lacunas para K ↓ e K ^′ ↑ elétrons são grandes devido a Δ _{η σ} = Δ _z - η σ λ _SO . Como U aumenta, todas as minibandas se movem gradualmente em direção à região de alta energia (ver Fig. 4a), e todos os intervalos de banda exibem oscilação amortecida com U (ver Fig. 4b). Quando U = σ h , o potencial efetivo é zero e a lacuna atinge o valor máximo. A lacuna é fechada no valor crítico de U , por conta do surgimento de novos pontos Dirac. A Figura 4c, d representa a dependência de minibandas e lacunas de banda na largura da barreira d _b em U =0. Na ausência de campo externo ( d _b =0), as minibandas continuam degeneradas e a lacuna no nível de Fermi é 2 λ _SO . Com o aparecimento de d _b , a minibanda é dividida, onde vale e giro tornam-se não degenerados. As minibandas de K ↑ (ou K ↓ ) e K ^′ ↓ (ou K ^′ ↑ ) elétrons mantêm simetria de espelho em torno de E =0 (ver Fig. 4c). Como d _b aumenta, as lacunas de K ↓ e K ^′ ↑ elétrons são ampliados gradualmente. As lacunas de K ↑ e K ^′ ↓ elétrons diminuem para zero quando d _b satisfaz d _b / d _w = λ _SO / Δ _z e, posteriormente, aumente com d _b (ver Fig. 4d). As larguras de lacunas se aproximam da saturação com o aumento adicional de d _b . Além disso, a largura da minibanda é reduzida como d _b aumenta (não mostrado na figura), devido ao menor acoplamento de estados próprios. O efeito do campo elétrico no gap é análogo ao do estudo anterior [50].

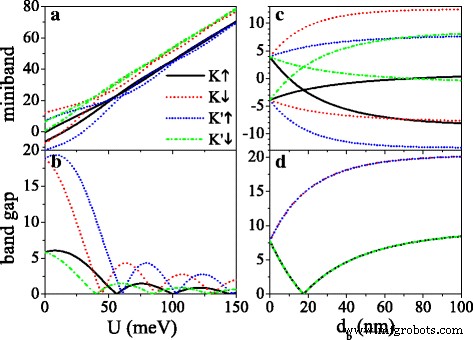
( a ) Minibandas perto do nível Fermi e ( b ) suas lacunas de banda no ponto Dirac original versus potencial U , em d _b = d _w =50 nm. ( c ) Minibandas perto do nível Fermi e ( d ) suas lacunas de banda no ponto Dirac original versus d _b , em U =0 e d _w =50 nm. Os valores de outros parâmetros são h =8,0 meV, Δ _z =15,0 meV e k _x = k _y =0

A velocidade do grupo depende fortemente dos índices de spin e vale, como mostrado na Fig. 5. Os componentes ( v _x , v _y ) de velocidade pode ser definida como
$$ \ begin {array} {@ {} rcl @ {}} v_ {x} / v_ {F} =\ parcial E / \ parcial k_ {x}, \ quad v_ {y} / v_ {F} =\ parcial E / \ parcial k_ {y}. \ end {array} $$ (13)

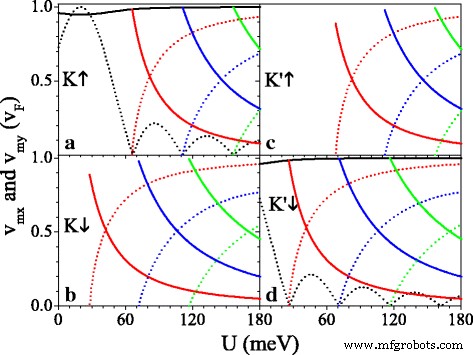
( a - d ) Velocidade versus potencial U , e os parâmetros são definidos como h =20,0 meV e Δ _z =7,8 meV. As curvas sólidas pretas, vermelhas, azuis e verdes são as velocidades v _{0 x} , v _{1 x} , v _{2 x} , e v _{3 x} , respectivamente. As curvas tracejadas pretas, vermelhas, azuis e verdes são as velocidades v _{0 y} , v _{1 y} , v _{2 y} , e v _{3 y} , respectivamente

A Figura 5 apresenta os componentes da velocidade v _mx e v _meu em unidades de v _F no ponto Dirac original ( m =0) e novos pontos Dirac ( m =1,2,3). Pode-se ver isso como U aumenta, v _{0 y} oscila de forma decadente e v _{0 x} ≈ v _F é quase afetado (ver Fig. 5a, d). No valor crítico de U onde os novos pontos de Dirac emergem, v _mx ≈ v _F mas v _{0 y} = v _meu =0, indicando um comportamento de colimação ao longo do k _x direção para spins e vales específicos. Quando U excede o valor crítico e aumenta ainda mais, v _meu aumentar para v _F mas v _mx diminuir para zero gradualmente. O efeito do potencial periódico é altamente anisotrópico, devido à natureza quiral. As características da velocidade anisotrópica são várias para diferentes spins e vales devido à lacuna Δ _{η σ} e o potencial U _σ , que pode ser comandado usando U . Tomando U =20 meV por exemplo, v _{0 y} = v _F para K ↑ elétron é muito maior do que v _{0 y} =0,16 v _F para K ^′ ↓ elétron, e não v _{0 y} para K ↓ e K ^′ ↑ elétrons devido ao gap. v _mx (ou v _meu ) para o elétron de spin-up é sempre maior (ou menor) do que para o elétron de spin-down no mesmo vale. Notavelmente, a Fig. 5 também implica que para um valor pequeno de U , v _{0 x} , v _{0 y} , e v _mx são menores que v _F devido a Δ _z e h , diferente do sistema sem intervalos [44]. Por exemplo, v _{1 x} =0,98 v _F , 0,89 v _F , 0,89 v _F e 0,98 v _F para K ↑ , K ↓ , K ^′ ↑ e K ^′ ↓ elétrons, respectivamente, quando o ponto de Dirac aparece. Para iluminar a influência de Δ _z e h na velocidade do grupo, a Fig. 6 mostra as velocidades ( v _{0 x} , v _{0 y} ) em função de (a) Δ _z e (b) h para K ↑ elétron. Da Fig. 6a podemos ver claramente que v _{0 x} está diminuindo monotonicamente com Δ _z enquanto v _{0 y} é insensível à mudança de Δ _z . Pelo contrário, v _{0 x} está insensível a h , enquanto v _{0 y} aumenta para o valor máximo v _{0 y} = v _F em h = σ U e então diminui com h . Os resultados indicam que a velocidade do grupo pode ser suprimida por Δ _z e h em siliceno.

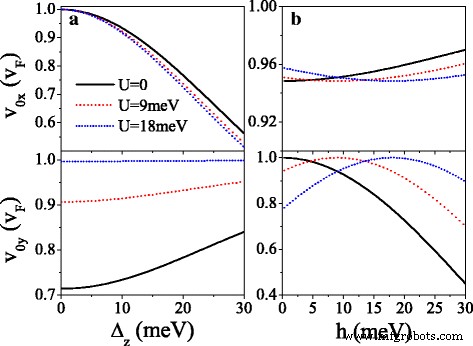
Velocidades v _{0 x} e v _{0 y} versus ( a ) Δ _z e ( b ) h , para K ↑ elétron. ( a ) h =20,0 meV e λ _SO = Δ _z / 2. ( b ) Δ _z =7,8 meV

Transporte Spin- and Valley-Polarized

A estrutura de banda dependente de spin e vale é refletida na propriedade de transporte e fornece um guia no controle do transporte. Nesta seção, discutimos as propriedades do transporte polarizado por spin e vale através de uma superrede de siliceno finita. A Figura 7 mostra a probabilidade de transmissão T _{η σ} para (a, c) K ↑ e (b, d) K ↓ elétrons, e o número do período n =10. As curvas tracejadas em vermelho são as minibandas, que também são as bordas dos diferentes estados eletrônicos que decidem a transmissão. Podemos ver que a transmissão é restrita na região da minibanda e nenhuma transmissão na região do gap (ver Fig. 7a, b). A distribuição da transmissão é simétrica em torno de k _y =0 devido às minibandas simétricas. A característica ressonante da transmissão surge dos estados ressonantes. Deve-se notar que a transmissão ainda existe na região da lacuna perto de k _y =0 devido ao efeito túnel de estados próprios. T _{η σ} no nível de Fermi para K ↑ e K ↓ elétrons são mostrados na Fig. 7c, d), respectivamente. Pode-se ver claramente que muitos picos ressonantes finos com T _{η σ} =1 ocorrem precisamente nas posições dos pontos de Dirac, sugerindo uma aplicação do sistema como um filtro de spin e vale.

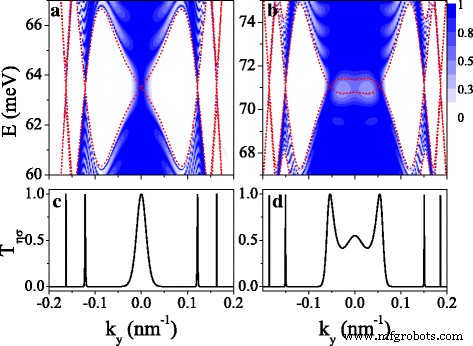
Gráfico de contorno da transmissão T _{η σ} ( E , k _y ) para ( a ), ( c ) K ↑ elétron e ( b ), ( d ) K ↓ elétron. Os valores dos parâmetros são iguais aos da Fig. 2 (d1 – d4) e n =10

A forte dependência da estrutura da banda nos índices de spin e vale é benéfica para a realização de polarizações de alto spin e vale. Figure 8 presents the minibands, conductances G _{η σ} , spin polarization P _s , and valley polarization P _v as a function of potential U . It can be found that the distribution of conductance is completely in agreement with the band structure, that is, the conductance (or conductance gap) corresponds to the miniband (or band gap). The minibands for spin-up and spin-down electrons could be alternative distribution by adjusting h devidamente. Consequently, $G_{K(K^{\prime })\uparrow }$ and $G_{K(K^{\prime })\downarrow }$ present alternative distribution as well, i.e., $G_{K(K^{\prime })\uparrow }$ nearly vanishes for those regions where $G_{K(K^{\prime })\downarrow }$ is in resonance and vice versa. This result directly leads to a remarkable spin polarization, proposing a switching effect of spin polarization (see Fig. 8a). By changing Δ _z , the minibands and conductances for electrons near K and K ^′ valleys could be controlled, leading to a fully valley-polarized current (see Fig. 8b). Compared with spin polarization, the valley polarization is not perfect enough. However, this drawback could be remedied via the disorder structure of the system, as discussed in the following.

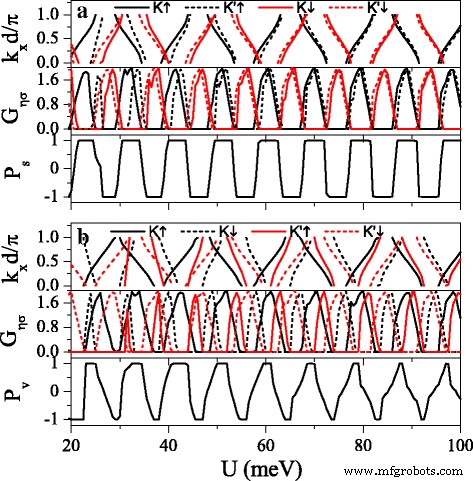
Minibands, conductances G _{η σ} , spin polarization P _s , and valley polarization P _v versus potential U . ( a ) Δ _z =4.0 meV. ( b ) Δ _z =12.0 meV. Other parameters are set as h =7.0 meV, E =6.0 meV, d _b =d _w =120 nm, and n =10

Figure 9 shows the (a) spin polarization P _s and (b) valley polarization P _v in (U ,h ) space. Interestingly, both P _s and P _v present periodical changes in the considered region, which is not observed in the ferromagnetic silicene junction [33]. Both distributions of P _s and P _v are antisymmetric with respect to h →−h . It is possible to achieve independently a full spin and valley polarization by a proper tuning of the fields U e h . For example, when h =6 meV and U =42 meV, P _s ≈1 and P _v ≈1, meaning that the current is mainly contributed by K ↑ electrons. When h =6 meV and U =44 meV, P _s ≈1 and P _v ≈−1 while P _s ≈−1 and P _v ≈−1 at h =6 meV and U =46 meV. The results demonstrate that a spin and valley polarization can be switched effectively.

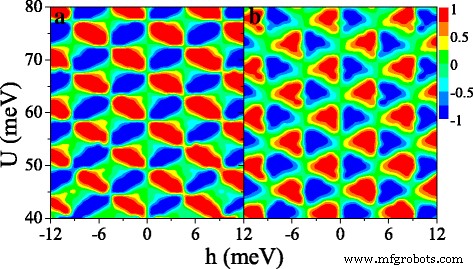
Contour plot of (a ) spin polarization P _s (U ,h ) e ( b ) valley polarization P _v (U ,h ), at Δ _z =10.0 meV. The values of other parameters are the same as these in Fig. 8

In experiment, the structural imperfection of the model is unavoidable due to the limitations of the experimental techniques. Therefore, it is necessary to discuss the effect of the disorder on transmission. When the electric field or exchange field presents disorder, the conductance, spin polarization, and valley polarization are shown in Figs. 10 and 11. We set disorder situations of Δ _z e h fluctuate around their mean values, given by 〈Δ _z 〉=Δ _{z 0} and 〈h 〉=h ₀ , respectivamente. The fluctuations are given by
$$\begin{array}{@{}rcl@{}} \Delta_{z} |_{i} =\Delta_{z0} (1 + \delta \zeta_{i}), \quad h |_{i} =h_{0} (1 + \delta \zeta_{i}), \end{array} $$ (14)

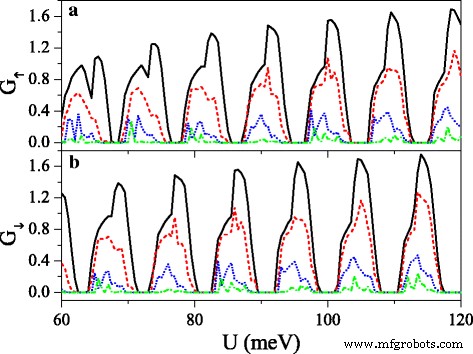
Conductances (a ) G _↑ and (b ) G _↓ versus potential U , when the electric field presents disorder, at n =50 and Δ _{z 0} =20.0 meV. The solid, dashed, dotted, and dash-dotted curves correspond to the disorder strength δ =0.0, 0.1, 0.3, and 0.6, respectively. The values of other parameters are the same as these in Fig. 8

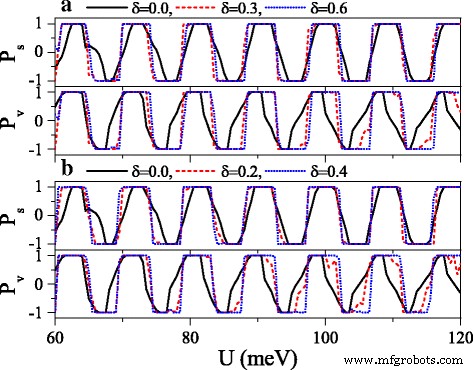
Polarizations P _s and P _v versus potential U when a the electric field or b the exchange field presents disorder. Δ _{z 0} =20.0 meV and h =7.0 meV in (a ) Δ _z =20.0 meV and h ₀ =7.0 meV in (b ) The values of other parameters are the same as these in Fig. 10

where {ζ _i } is a set of uncorrelated random variables or white noise, − 1<ζ _i <1, δ is the disorder strength, and i is the site index. Note that the disorder only takes place in the x direction, and the system is always homogeneous in y direção. Thus, k _y still keeps conservation. Figure 10 exhibits the effect of the disorder of the electric field on the conductances (a) G _↑ and (b) G _↓ . With the presence and increase of the disorder strength δ , both G _↑ e G _↓ are suppressed gradually, and each resonant peak splits into many small peaks. One may find that the conductance range is narrowed while the conductance gap range is broadened. Hence, the allowable (or forbidden) ranges of G _↑ completely fall into the forbidden (or allowable) ranges of G _↓ , giving rise to an excellent spin polarization (see Fig. 11). Furthermore, the positions of conductances and conductance gaps are nearly invariable as δ changes, suggesting that the miniband and band gap are insensitive to the disorder. Note that the disorder effect of the electric field on G _K e G _K ^′ is similar to that observed in Fig. 10. Figure 11 presents the disorder effects of (a) the electric field and (b) the exchange field on polarizations P _s and P _v . Obviously, with the increase of δ , P _s and P _v increase greatly, and the polarization platform is broadened. Thus, a full spin and valley polarization is realized. Comparison between Fig. 11a and b indicates that the disorder effect of exchange field is more prominent. The results demonstrate that the disorder could enhance the spin and valley polarizations compared with the order case, which is an advantage in realistic application.

Conclusões

In summary, we demonstrated detailedly that band structure and transport property of silicene under a periodic field strongly depend on the spin and valley degrees of freedom. The numerical results indicate that electrons with different spins and valleys have various characteristics in Dirac point, bang gap, and group velocity. In particular, owing to the electric field and exchange field, the anisotropic velocity is restrained, which displays a collimation behavior for specific spins and valleys. Therefore, the transmission presents strong spin- and valley-dependent feature, consistent with the band structure, resulting in a significant spin and valley polarizations. In addition, the disorder could greatly enhance the spin and valley polarizations. Finally, we hope these results can be conducive to the potential applications of the spin and valley indices.

Abreviações

2D:: Bidimensional
FM:: Ferromagnetic
SOI:: Spin-orbit interaction

Reduza a sensibilidade do CL-20 melhorando a condutividade térmica por meio de nanomateriais de carbono Sensor de deformação ultrassensível baseado em filme piezoelétrico de poli (fluoreto de vinilideno) flexível

Nanomateriais

Materiais Poliméricos

biológico

Corante

Especiarias