Efeito da morfologia e estrutura cristalina na condutividade térmica dos nanotubos de Titânia

Resumo

Nanotubos de titânia (TNTs) com morfologia e estrutura cristalina diferentes são preparados por métodos de processamento químico e anodização rápida (RBA). Os nanotubos são estudados em termos de condutividade térmica. Os TNTs com espessura de parede variável abaixo de 30 nm reduziram significativamente a condutividade térmica do que o titânia em massa, devido ao confinamento de fônons, menor caminho livre médio de fônons e espalhamento aprimorado de contornos de fônons. Os nanotubos amorfos (TNT _Amor ) têm paredes comparativamente mais espessas do que ambos os nanotubos cristalinos. O TNT _Amor tem uma condutividade térmica de 0,98 W m ⁻¹ K ⁻¹ , que é ligeiramente menor do que a condutividade térmica dos nanotubos de anatase cristalina (TNT _A ; 1,07 W m ⁻¹ K ⁻¹ ) No entanto, os nanotubos de titânia com estrutura mista (TNT _{A, T} ) e as menores dimensões têm a menor condutividade térmica de 0,75 W m ⁻¹ K ⁻¹ , provavelmente devido ao confinamento do fônon. Os resultados experimentais são comparados com o estudo teórico considerando o efeito de confinamento de tamanho com diferentes dimensões de parede de TNTs e espalhamento de superfície. Os resultados concordam bem com o fator de rugosidade da superfície ( p ) de 0,26 para TNT _{A, T} , 0,18 para TNT _A e 0,65 para TNT _Amor , indicando espalhamento difusivo de fônons e superfícies mais ásperas para TNT _A . Curiosamente, os presentes resultados em conjunto com os apresentados na literatura sugerem que a redução da condutividade térmica em relação à espessura da parede ocorre também para os nanotubos amorfos. Isso é atribuído ao papel dos propagons no transporte térmico de estruturas desordenadas.

Histórico

Devido à persistente miniaturização dos dispositivos eletrônicos e sistemas nanoeletromecânicos (NEMS), o estudo das nanoestruturas e suas propriedades têm atraído muita atenção nos últimos anos [1, 2]. Os estudos sobre o controle do tamanho e nucleação de nanoestruturas foram apresentados anteriormente, como nanoestruturas têm sido utilizadas para diferentes aplicações potenciais [3, 4]. A pesquisa sobre o controle das propriedades térmicas em nanoestruturas pelo controle do tamanho, composição e estrutura é de particular interesse devido às suas aplicações na indústria eletrônica, NEMS e termoelétrica avançada [2, 5, 6]. Um caso particular é minimizar a dissipação de calor nos circuitos integrados (ICs) para sua estabilidade e longa vida útil.

Materiais unidimensionais (1D), como nanotubos de carbono (CNT), possuem uma condutividade térmica à temperatura ambiente de 3000 W m ⁻¹ K ⁻¹ , que é muito maior do que um cristal de diamante [2, 5]. O CNT é uma folha de grafeno sem costura e tem maior condutividade térmica devido à forte ligação carbono-carbono e sem defeitos pontuais e limites [6]. Ao contrário do CNT, outros semicondutores cristalinos unidimensionais têm transporte térmico significativamente reduzido em comparação com o material a granel [6]. Esta diminuição na condutividade térmica nas nanoestruturas de baixa dimensão é atribuída à redução no caminho livre médio do fônon (MFP), tamanho de grão pequeno, espalhamento de contorno de fônon, rugosidade e defeitos pontuais [6,7,8].

Nanofios de silício têm sido estudados para adaptar o transporte térmico para sua utilização em aplicações termoelétricas. Pela primeira vez, Li et al. [9] relataram condutividades térmicas duas vezes mais baixas para nanofios de silício em comparação com silício bruto devido ao espalhamento de contorno de fônon. A condutividade térmica dos nanofios de silício com diâmetro de 50 nm se aproximou do limite amorfo do silício, com redução de 100 vezes da condutividade térmica em comparação ao silício bruto [10]. Esses nanofios de silício com condutividade térmica consideravelmente reduzida e maior condutividade elétrica possuem maior eficiência termoelétrica [10,11,12,13]. As propriedades térmicas reduzidas de outros nanofios em comparação com seus materiais a granel também são relatadas, como Bi ₂ Te ₃ [14, 15], Si / SiGe [16], Ge / SiGe [17, 18], ZnTe [19], GaN [20], InSb [21], CdS [22], PbS, PbSe [23], InAs [24], Bi [25], SrTiO ₃ [26], ZnO [27] e TiO ₂ nanofios [28, 29]. Além disso, os estudos térmicos em nanotubos como Si [30], Bi ₂ Te ₃ [31], e TiO ₂ nanotubos [1, 32,33,34] foram relatados. Com base nesses estudos, pode-se concluir que a condutividade térmica dos nanotubos é menor do que a dos nanofios correspondentes devido ao espalhamento adicional de fônons dentro das paredes dos nanotubos [31]. Deve-se notar que a condutividade térmica dos nanotubos cristalinos é geralmente maior do que a de suas contrapartes amorfas e fortemente influenciada pela rugosidade de sua superfície [32, 34]. Além disso, Wingert et al. [30] notaram que os nanotubos de silício cristalino têm menor condutividade térmica do que seus equivalentes amorfos. Esta observação da condutividade térmica além do limite amorfo em nanotubos de silício cristalino foi atribuída ao amolecimento elástico e forte espalhamento de contorno de fônon [30]. O transporte térmico nos nanomateriais amorfos é atribuído principalmente (93%) aos difusões (modos "diffuson" de não propagação), enquanto o restante 4% está relacionado aos modos semelhantes a fônons conhecidos como "propagões" e 3% aos modos localizados conhecido como “locons” [35]. Uma vez que o caminho livre médio dos difusões é geralmente considerado como sendo o da distância interatômica, espera-se que a condutividade térmica das nanoestruturas amorfas seja independente das dimensões [36].

Cahill e Pohl propuseram um modelo de condutividade térmica mínima bem conhecido para os materiais desordenados [37]. De acordo com esse modelo, a condutividade térmica mínima proposta (limite amorfo) da titânia é 1,6 W m ⁻¹ K ⁻¹ [38]. Nenhuma redução dependente do tamanho na condutividade térmica de óxidos amorfos foi relatada [35], embora alguns filmes de óxido tenham sido alegados como tendo condutividade térmica abaixo do limite amorfo. A razão para o menor valor de condutividade térmica obtido foi atribuída às impurezas na estrutura ou no caso de filmes finos à resistência térmica do contorno entre o filme e o substrato [35].

Nanotubos de Titânia - nanoestruturas 1D com uma alta área de superfície específica - foram projetados para uma série de aplicações potenciais [39]. Nanotubos de titânia podem ser sintetizados por vários métodos, incluindo hidrotérmico [40] e anodização eletroquímica [39, 40], processamento químico [41], anodização de decomposição rápida (RBA) [42] e métodos assistidos por modelo e eletrofiação [40]. Condutividade térmica na faixa de 0,40–0,84 W m ⁻¹ K ⁻¹ [1] e 0,55–0,75 W m ⁻¹ K ⁻¹ [33] foram observados para nanotubos de titanato sintetizados pelo processo hidrotérmico. Brahmi et al. [32] relatou uma condutividade térmica de 0,85 W m ⁻¹ K ⁻¹ para um único nanotubo amorfo e 1,5 W m ⁻¹ K ⁻¹ para nanotubo de titânia anatase preparado por anodização eletroquímica. Por outro lado, as matrizes de nanotubos de titânia destacadas foram relatadas como tendo uma condutividade térmica de 0,617 W m ⁻¹ K ⁻¹ ao longo da direção do tubo para amorfo e 1,12 W m ⁻¹ K ⁻¹ para nanotubos de anatase [34]. A condutividade térmica amorfa do tubo cruzado foi de 0,077–0,1024 W m ⁻¹ K ⁻¹ para nanotubos amorfos e 0,24 W m ⁻¹ K ⁻¹ no caso de nanotubos cristalinos [34]. Matrizes de nanotubos de titânia nestes relatórios são cultivadas em substrato de Ti pelo método de anodização eletroquímica usando eletrólitos orgânicos com íons de flúor (terceira geração de TNTs) com uma espessura de parede de 30-70 nm [32] e 15 nm [34]. Os nanotubos preparados pelo RBA compreendem a quarta geração de TNTs [43], onde feixes de nanotubos de titânia são obtidos utilizando um eletrólito livre de fluoreto [42].

Na presente contribuição, relatamos um estudo experimental comparativo sobre a condutividade térmica de nanotubos de titânia com morfologia variável, estrutura cristalina e espessura de parede abaixo de 30 nm. Os nanotubos são sintetizados por processamento químico [41] e RBA [42]. A pesquisa de condutividade térmica se estende à quarta geração de nanotubos de titânia (ou seja, pós preparados por RBA) e à comparação de pós de TNT por diferentes métodos de síntese. Liang e Li [44] propuseram um modelo analítico de condutividade térmica dependente do tamanho para nanomateriais, que foi confirmado experimentalmente para nanofios e filmes. O modelo foi posteriormente modificado por Gao e Jelle [1] para nanotubos, mas não foi verificado experimentalmente. De acordo com o modelo, a condutividade térmica dos nanotubos é dependente da espessura da parede [1]. Brahmi et al. [32] estudaram a condutividade térmica de TNTs com uma espessura de parede variável de 30-70 nm; entretanto, redução da condutividade térmica com a espessura da parede não foi observada em seu estudo. No presente relatório, verificamos experimentalmente a condutividade térmica dependente do tamanho dos nanotubos de titânia, reduzindo as dimensões da parede nos nanotubos de titânia cristalinos. Ao contrário da percepção geral, os dados atuais combinados com aqueles apresentados na literatura sugerem uma redução dependente do tamanho da condutividade térmica também para nanotubos de titânia amorfos.

Métodos / Experimental

Síntese de TNTs

Os pós de nanotubos de titânia (TNT) foram preparados usando métodos de processamento químico e anodização de decomposição rápida (RBA), conforme discutido em detalhes em [41, 42], respectivamente. Três tipos de nanotubos de titânia com estrutura cristalina e morfologia diferentes foram preparados, ou seja, (i) TNTs de paredes múltiplas abertas, (ii) TNTs amorfos de parede única com uma extremidade aberta e a outra fechada, e (iii) nanotubos de titânia cristalinos com uma extremidade aberta e a outra fechada. Os nanotubos de titânia de extremidade aberta com múltiplas paredes foram preparados pelo método de processamento químico e tinham uma estrutura cristalina mista de titanato (Na _x H _{2 - x} Ti ₃ O ₇ · NH ₂ O, onde 0 < x <2) com picos proeminentes da fase anatase [41] e denominado como TNT _{A, T} ao longo do texto. Outros dois tipos de nanotubos foram preparados pelo método RBA usando eletrólito à base de água (ácido perclórico 0,1 M) para obter TNTs cristalinos com estrutura anatase ou eletrólito orgânico (etilenoglicol + água + ácido perclórico) para produzir nanotubos amorfos [42] . O amorfo (TNT _Amor ) e cristalino (TNT _A ) os pós de nanotubos de titânia produzidos pela RBA são de parede única com uma extremidade aberta e a outra fechada. A ilustração esquemática desses TNTs é mostrada na Fig. 1.

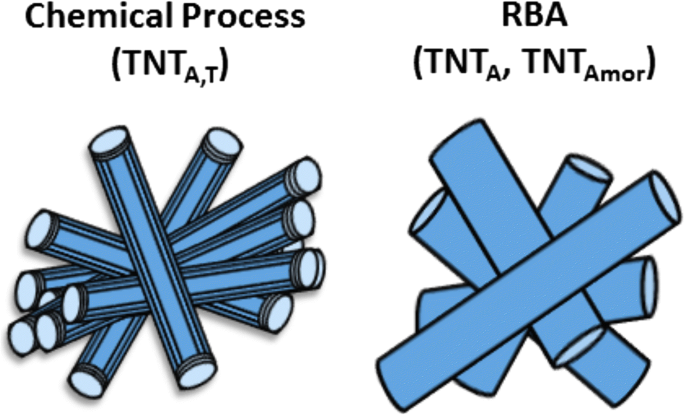
Ilustração esquemática de TNT _{A, T} , TNT _A e TNT _Amor

Métodos de caracterização

A morfologia e o tamanho dos pós de nanotubos de titânia foram examinados usando microscopia eletrônica de transmissão (TEM; Tecnai F-20 G2 200 kV FEG S-twin GIF) em uma tensão operacional de 200 kV. A estrutura cristalina foi obtida por difração de raios X (XRD). Os dados de XRD foram obtidos usando um difratômetro PANalytical X’pert Pro. O comprimento de onda operacional foi de radiação Cu-Kα 0,154 nm, com tensão e correntes de 40 kV e 45 mA, respectivamente. A densidade de cada pó foi medida por Pycnometer (Upyc 1200e v5.04; Quantachrome Corporation). Os pós foram então comprimidos em pelotas de 10 mm para medições de condutividade térmica. As pelotas foram feitas por prensagem hidrostática de nanotubos em pó e a espessura das pelotas obtidas estava na faixa de 2–4 mm. A espessura medida e a densidade calculada das pelotas estão relacionadas à pressão aplicada, que foi controlada em uma faixa de 5 a 50 kN para ajustar a densidade de cada pelota. As superfícies dos peletes foram analisadas por microscópio eletrônico de varredura de canhão de emissão de campo (FEG-SEM; Hitachi S-4700).

A difusividade térmica dos peletes foi medida usando o método de flash de luz utilizando equipamento Netzsch LFA 467 com software Proteus LFA em temperatura ambiente. Um curto pulso de laser de xenônio aqueceu a superfície posterior das pelotas. Antes das medições, os pellets foram revestidos com spray de grafite para melhorar a absorção e emissão da radiação térmica. Um detector infravermelho observou a mudança de temperatura correspondente no lado oposto do pellet. De acordo com Parker et al. [45], a seguinte relação pode ser usada para obter difusividade térmica a partir dos dados experimentais:
$$ \ alpha =\ frac {0,1338 \ {d} ^ 2} {t ^ {1/2}} $$ (1)
Aqui, α é a difusividade térmica da amostra, d é a espessura da amostra e t ^1/2 é o valor de tempo na altura da metade do sinal. As medições de LFA foram repetidas cinco vezes por amostra. O software Proteus foi utilizado para ajuste das medidas. A condutividade térmica da amostra foi obtida usando a seguinte relação [45]:
$$ \ kappa (T) =\ alpha (T) \ {c} _p (T) \ \ rho (T) $$ (2)
Aqui, κ denota a condutividade térmica, α denota a difusividade térmica, c _p é a capacidade de calor específica, e ρ é o valor da densidade. A capacidade térmica específica dos nanotubos de titânia se aproxima daquela do dióxido de titânio bruto acima de 100 K [46] e, portanto, os valores da capacidade térmica específica para os nanotubos de titânia foram adotados a partir de um estudo de Guo et al. [34, 47]. A densidade dos peletes foi calculada a partir do peso e do volume correspondente dos peletes. A incerteza nos resultados experimentais advém dos erros da unidade de medição LFA para medições de difusividade (2%) e do cálculo da espessura de pellets por um micrômetro. O erro total para os experimentos de condutividade térmica foi estimado em 8%.

Resultados e discussão

Os dados de XRD para a estrutura cristalina dos nanotubos são mostrados na Fig. 2. O TNT _Amor os dados não têm picos confirmando a estrutura amorfa dos nanotubos preparados por RBA utilizando um eletrólito orgânico [42]. Os nanotubos quimicamente processados ​​(TNT _{A, T} ) mostram picos proeminentes da fase anatase junto com H ₂ Ti ₃ O ₇ picos. A estrutura diferente de anatase foi atribuída como Na _x H _{2 - x} Ti ₃ O ₇ · NH ₂ O onde 0 < x <2, conforme relatado em um estudo anterior [41]. O TNT _A preparado por eletrólito à base de água têm picos de anatase. A partir dos dados de XRD, é óbvio que dois tipos de nanotubos são cristalinos e um é amorfo.

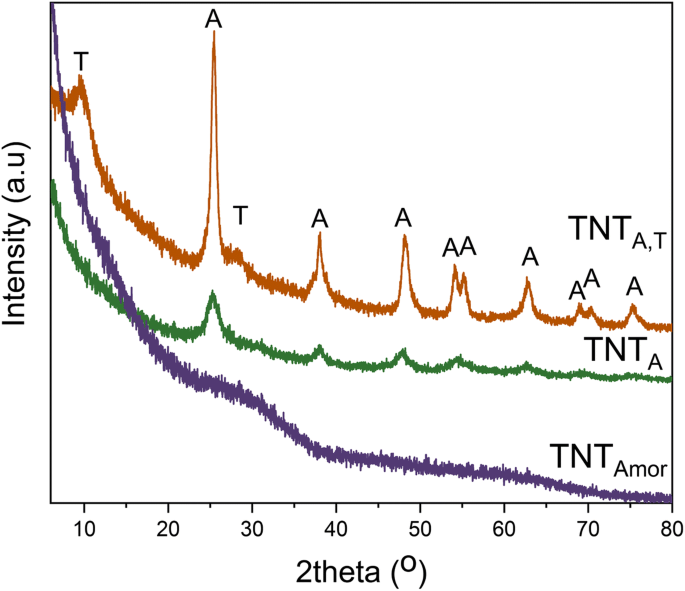
XRD de nanotubos de titânia cristalinos que consistem em anatase (TNT _A ), titanato e anatase (TNT _{A, T} ) e estrutura amorfa (TNT _Amor ) [41, 42]. T =H ₂ Ti ₃ O ₇ , A =picos de anatase

Os nanotubos de titânia sintetizados pelo método de processamento químico são multifacetados devido à rolagem das nanofolhas durante a síntese dos nanotubos [48]. Esses nanotubos abertos têm uma espessura de parede de 4-5 nm com um comprimento variável de 60 a centenas de nanômetros [41]. Imagens TEM desses nanotubos são mostradas na Fig. 3a, b. Os nanotubos são orientados aleatoriamente e preferem ficar em pacotes como mostrado na Fig. 3a. A estrutura de paredes múltiplas de 3 a 4 camadas é evidente, conforme representado na Fig. 3b. Os nanotubos cristalinos produzidos por RBA têm uma espessura de parede na faixa de 7–12 nm e são 18–35 μm de comprimento [42] (Tabela 1). Eles são de parede única com uma extremidade aberta e outra fechada como mostrado na micrografia na Fig. 3c, onde a inserção mostra a extremidade aberta. Os nanotubos amorfos produzidos pelo RBA possuem morfologia semelhante aos nanotubos cristalinos preparados pelo método RBA. No entanto, as dimensões são diferentes devido à contribuição do eletrólito. A espessura da parede está na faixa de 15–30 nm e o comprimento tubular está na faixa de 6–13 μm [42]. A Figura 3d mostra a imagem TEM do nanotubo amorfo de parede única. A rugosidade é o valor médio para o desvio da altura da superfície da parede TNT do plano de referência [44]. Os valores médios de rugosidade estimados a partir de imagens TEM dos TNTs são de aproximadamente 0,3 nm para TNT _{A, T} , 1,0 nm para TNT _A e 1,5 nm para TNT _Amor .

Imagens TEM de a o TNT _{A, T} preparado por processamento químico, b Micrografia HR-TEM mostrando a estrutura de nanotubos de paredes múltiplas, c os nanotubos cristalinos de parede única preparados (TNT _A ) por RBA e d os nanotubos amorfos (TNT _Amor )

Os pellets de nanotubos de titânia foram preparados em diferentes densidades e porosidades correspondentes usando uma prensa hidráulica. TNT _Amor o pó foi compactado com carga máxima de 20 kN porque com cargas mais altas a superfície lisa dos grânulos necessária para as medições de LFA não foi obtida. A porosidade dos peletes é calculada pelo seguinte (Eq. 1):
$$ P =\ frac {\ rho_o- \ rho} {\ rho_o} $$ (3)
onde ρ _o é a densidade das amostras a granel, que é a densidade do pó obtida por medições de picnômetro e mostrada na Tabela 1. O ρ é a densidade calculada do pellet e P é a porosidade das amostras. As superfícies dos pellets foram estudadas com FESEM no arquivo Adicional 1. As análises das superfícies mostram a orientação aleatória dos feixes de nanotubos (Arquivo Adicional 1:Figura S1) na superfície, ou seja, os nanotubos podem ser observados em várias orientações (topo aberto, fundo fechado e posições de vista lateral) no arquivo adicional 1:Figura S1. Imagens SEM semelhantes de superfícies de pellets de TNT _A , TNT _Amor , e TNT _{A, T} pellets são representados no arquivo adicional 1:Figura S2a – c. A difusividade térmica medida pelo método LFA é resumida na Tabela 2. As condutividades térmicas medidas são plotadas como uma função da porosidade, como mostrado na Fig. 4. A condutividade térmica medida diminui com o aumento da porosidade para todas as amostras (Tabela 2). Gao e Jelle obtiveram tendência semelhante para os valores de condutividade térmica de amostras com diferentes porosidades de pellets [1]. Uma clara redução da condutividade térmica é obtida para os nanotubos em comparação com o titânio bruto (8,5 W m ⁻¹ K ⁻¹ [34]). Esta supressão da condutividade térmica em nanotubos de titânia 1D é atribuída ao confinamento do fônon e ao espalhamento da fronteira do fônon devido à redução do tamanho [1]. Como os nanotubos são orientados aleatoriamente e compactados para formar pellets, eles também estão conectados uns aos outros. Nesse caso, o espalhamento de fônons na área interconectada entre os nanotubos e a resistência Kapitza também afeta os valores gerais de condutividade térmica. No entanto, a resistência de contato Kapitza e o espalhamento de contorno de fônon considerando a orientação dos nanotubos são ignorados aqui para simplificar.

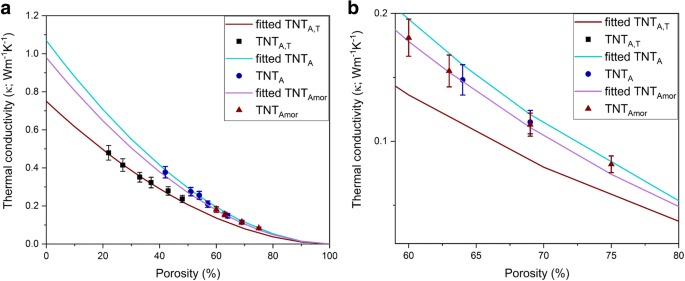
a Condutividade térmica efetiva medida dos nanotubos de titânia (símbolos) versus porosidade. As linhas sólidas representam o ajuste usando o modelo de condutividade térmica efetiva (Eq. 6) com um fator de forma de 1,24. b Condutividade térmica na faixa de 60-80% de porosidade para clareza

A condutividade térmica medida de uma amostra estima a condutividade dos pellets de nanotubos considerando os nanotubos de titânia e os poros preenchidos com ar. A condutividade térmica do ar é presumida como 0,026 W m ⁻¹ K ⁻¹ [1] A condutividade térmica dos nanotubos ( κ _TNTs ), excluindo o impacto da porosidade, pode ser estimado usando modelos de condutividade térmica efetiva fornecidos pela Eq. 4 [1, 49], que para o caso de poros não condutores reduz para a Eq. 5 [1]:
$$ {\ kappa} _ {TNTs} =\ frac {\ upkappa_ {eff} - {\ upkappa} _ {air} \ cdot P} {\ left (1-P \ right)} $$ (4) $$ {\ kappa} _ {TNTs} =\ frac {\ upkappa_ {eff}} {\ left (1-P \ right) \ kern0.5em} $$ (5)
onde κ _eff é a condutividade térmica efetiva que inclui o efeito de porosidade, κ _ar é a condutividade térmica do ar, e P é a porosidade. A condutividade térmica de TNT _{A, T} estimado a partir da Eq. 4 está no intervalo de 0,44–0,61 W m ⁻¹ K ⁻¹ para TNT _{A, T} . Usando o modelo de condutividade térmica efetiva (Eq. 4), a condutividade térmica de nanotubos de titanato puro com dimensões aproximadamente semelhantes foi relatada como 0,40–0,84 W m ⁻¹ K ⁻¹ [1] Nossos resultados concordam bem com os valores relatados quando o mesmo modelo efetivo de condutividade térmica (Eq. 4) é usado.

No entanto, a forma das lacunas de ar no compacto de nanotubos é apenas parcialmente aleatória, pois os próprios tubos têm uma forma não aleatória. A fim de dar conta da forma diferente dos poros, um modelo analítico aplicável para uma gama completa de porosidades foi derivado por Bauer [49] com base na resolução da equação de condução de calor de Laplace. Esta equação pode ser apresentada da seguinte forma:
$$ \ frac {\ kappa_ {eff}} {\ kappa_ {TNTs}} ={\ left (1-P \ right)} ^ {\ frac {3 \ varepsilon} {2}} $$ (6)
Nesta equação, ε é o fator de forma ou fator de correção relacionado ao formato dos poros. Seu valor explica as formas variáveis ​​dos poros. Para formas aleatórias de entreferro, ε é 2/3 [1, 27, 50], reduzindo assim a Eq. 5 a Eq. 6

Os valores dos fatores de forma foram estimados para formas poliédricas por Yang et al. [50], com base na modelagem de fatores de forma entre 1 e 1,48. Ao ajustar nossos dados à Eq. 6, o melhor ajuste (ver Fig. 4) é obtido para o fator de forma ε tendo o valor de 1,24. Com base no ajuste, a condutividade térmica para TNT _A encontrado para ser 1,07 W m ⁻¹ K ⁻¹ . Este valor é um pouco menor do que os valores relatados anteriormente, 1,12 W m ⁻¹ K ⁻¹ para matrizes de nanotubos anatase [34] e 1,5 W m ^{- 1} K ^{- 1} para um único nanotubo de anatase [32]. Correspondentemente, a condutividade térmica de TNT _Amor encontrado para ser 0,98 W m ⁻¹ K ⁻¹ . O valor ligeiramente inferior de condutividade térmica nos nanotubos amorfos em comparação com TNT _A é atribuído à sua estrutura amorfa. Valores mais baixos de condutividade térmica de nanotubos de titânia amorfos do que os dos nanotubos cristalinos também foram relatados em [32, 34]. Geralmente, filmes e materiais amorfos são conhecidos por terem menor condutividade térmica em comparação com materiais cristalinos, embora em pequena escala outros fatores também influenciem os valores de condutividade térmica. Por exemplo, Wingert et al. [30] relataram condutividade térmica 30% menor para os nanotubos de silício cristalino em comparação com suas contrapartes amorfas com dimensões semelhantes. A condutividade térmica subamorfa desses nanotubos foi atribuída ao forte efeito de amolecimento elástico nos nanotubos cristalinos [30]. Para comparação com os filmes amorfos, a condutividade térmica medida do filme de titânia amorfo de 100 nm depositado pelo processo ALD foi de 1,29 W m ⁻¹ K ⁻¹ [47]. A condutividade térmica aproximada pelo modelo de Cahill e Pohl da condutividade térmica mínima [37] foi de 1,38 W m ⁻¹ K ⁻¹ para o mesmo filme [47]. A condutividade térmica de filmes de titânia amorfa depositados por pulverização catódica foi relatada como 1,6 W m ⁻¹ K ⁻¹ para filmes de espessura de 920 nm [38, 51]. A condutividade térmica obtida para os nanotubos é menor do que a dos filmes amorfos de titânia tratados nestes relatórios [38, 47, 51]. No entanto, condutividade térmica comparativamente mais baixa de 0,7 W m ⁻¹ K ⁻¹ [52] também foi relatado para filme de titânia amorfo de 150 nm de espessura preparado por pulverização catódica e 0,9 W m ⁻¹ K ⁻¹ [53] para filme de 120 nm de espessura preparado pelo método sol-gel. No caso dos filmes, a resistência de contorno térmico entre o substrato, o filme fino e o filme do transdutor metálico foi considerado para diminuir a condutividade térmica geral abaixo do limite amorfo [52]. No caso dos nanotubos, fatores como resistência de contato térmico entre os nanotubos, rugosidade da superfície e impurezas na estrutura devido ao processo de preparação também afetam a condutividade térmica líquida. Guo et al. [34] propôs o maior valor de resistência de contato térmico entre arranjos de nanotubos amorfos em comparação com os nanotubos cristalinos. Condutividade térmica de 0,85 W m ⁻¹ K ⁻¹ foi relatado para um único nanotubo amorfo [32], enquanto Guo et al. [34] relatou a condutividade térmica de 0,617 W m ⁻¹ K ⁻¹ para matrizes de nanotubos amorfos ao longo da direção do tubo. Para TNT _{A, T} , condutividade térmica de 0,75 W m ⁻¹ K ⁻¹ é obtido. Este valor concorda bem com os resultados publicados para nanotubos de titanato [1,33] preparados por método hidrotérmico. É também notado que a condutividade térmica aumenta com o aumento da densidade do material mostrado na Tabela 1. A densidade medida de TNT _A (3,79 g cm ⁻³ ) está próximo da densidade de anatase em massa de 3,89 g cm ⁻³ [34]. A densidade de TNT _{A, T} também se correlaciona bem com a densidade medida de titanato misto e compactos de nanoestrutura de titânia [54]. O TNT _Amor tem uma densidade de 3,67 g cm ⁻³ , que está perto da densidade relatada do filme de titânia amorfo (3,73 g cm ⁻³ ) depositado por ALD [55]. A dependência linear da condutividade térmica com a densidade já foi relatada para filmes de alumina antes [55].

O caminho livre médio do fônon foi calculado como 2,5 nm para titânia [1], 1,21–3,15 nm para nanofibras de titânia [28] e 2–3 nm para nanotubos de titânia [32]. Dos três diferentes tipos de nanotubos estudados no presente relatório, os nanotubos de anatase (TNT _A ) produzem o maior valor de condutividade térmica, enquanto a condutividade térmica de TNT de paredes múltiplas _{A, T} é menor que TNT _A e TNT _Amor . A comparação dos valores de condutividade térmica presentes e publicados anteriormente em relação à espessura da parede de TNTs é mostrada na Fig. 5. Os TNTs produzidos a partir do método hidrotérmico, [1, 33] arranjos anodizados de terceira geração [34] e nanotubo único [ 32], e os valores dos nanotubos produzidos pelo presente RBA e métodos de processamento químico são plotados com seus valores médios de espessura de parede e condutividades térmicas (Fig. 5). A Figura 5 mostra que a condutividade térmica dos nanotubos de titânia cristalinos é reduzida significativamente, reduzindo a espessura da parede. A supressão da condutividade térmica com a redução da espessura da parede é atribuída ao confinamento do fônon com a espessura da parede [32]. Embora esse efeito não tenha sido observado por Brahmi et al. [32], obviamente devido à limitação de amostras com dimensões reduzidas, a redução proposta é observada com o presente TNT _{A, T} . A Figura 5 mostra uma tendência semelhante para nanotubos amorfos com a redução da condutividade térmica com a espessura da parede. Geralmente, espera-se que os nanomateriais amorfos tenham uma condutividade térmica semelhante independente da escala, uma vez que o transporte térmico é atribuído aos difusões não propagantes [47]. Dependendo do material e de suas dimensões, os propagões (propagação de vibrações) também podem contribuir para a condutividade térmica geral [35]. Wingert et al. [35] propôs a redução da condutividade térmica para filmes de silício amorfo, diminuindo a espessura do filme de micrômetro para nanômetro. Posteriormente, a redução da condutividade térmica dependente do tamanho para o silício amorfo foi confirmada experimentalmente por Kwon et al. [36] devido à contribuição dos propagons no transporte térmico geral. O caminho livre médio dos propagões para o silício amorfo foi encontrado na faixa de 10 nm a 10 μm e eles contribuíram para um aumento de 30% na condutividade térmica à temperatura ambiente [36]. O caminho livre médio da titânia amorfa foi estimado estar na faixa de 0,195–0,201 nm (distância interatômica ≈) [56]. Nenhum estudo foi encontrado informando o caminho livre médio dos propagões na titânia. No entanto, a redução da condutividade térmica com a diminuição da espessura da parede também é observada para TNTs amorfos (Fig. 5). Especula-se, portanto, que o transporte térmico em TNTs é atribuído não apenas aos difusões, mas os propagões também podem contribuir para a condutividade térmica geral, o que reduz a condutividade térmica dos nanotubos amorfos com a redução das dimensões da parede.

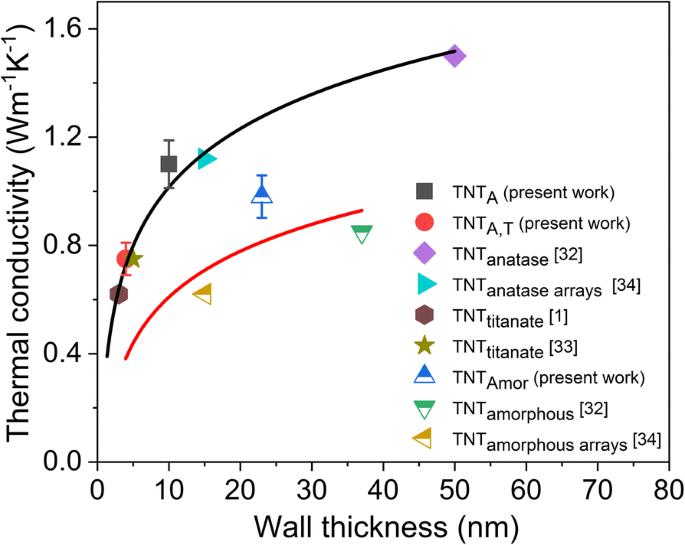
A condutividade térmica de nanotubos de titânia cristalinos e amorfos com relação à espessura de sua parede. As linhas de tendência são adicionadas para uma orientação visual

Foi proposto que as propriedades térmicas dos nanotubos são dependentes de sua espessura de parede ao invés do diâmetro [1, 32]. Gao e Jelle apresentaram uma aproximação teórica para a redução da condutividade térmica com a espessura da parede [1], que foi uma modificação de um modelo proposto anteriormente [44]. No entanto, a condutividade térmica geral também foi afetada pela rugosidade da superfície do nanotubo. Liang e Li [44] propuseram a fórmula analítica para condutividade térmica de nanomaterial semicondutor, incluindo efeitos de confinamento de tamanho, comprimento de cristalinidade e o espalhamento de fônons pela superfície pelo parâmetro de rugosidade da superfície ( p ) do seguinte modo:
$$ \ frac {\ kappa_ {TNT}} {\ kappa_B} =p \ cdot \ exp \ left (- \ frac {l_o} {L} \ right) \ cdot {\ left [\ exp \ left (\ frac { 1- \ alpha} {\ frac {L} {L_o} -1} \ right) \ right]} ^ {3/2 \ operatorname {}} $$ (7)
onde κ _TNT é a condutividade térmica do nanomaterial, κ _B é a condutividade térmica em massa, l _o é o phonon significa caminho livre, L é a espessura da parede, e L _o é o tamanho crítico no qual quase todos os átomos de um cristal estão localizados em sua superfície [44]. It should be noted that L _o  = 2(3 − d )w , where d is the dimension of the material (which is 1 in the case of nanotubes) and w is the atomic or molecular diameter [1, 44]. Finally, α is a material constant = 2Sv /3R  +  1, where Sv is the bulk vibrational entropy and R is the ideal gas constant [44]. The phonon mean free path of the titania nanotubes calculated from the kinetic formula of lattice thermal conductivity was reported to be 2.5 nm [1]. The bulk thermal conductivity of titania (κ _B ) is 8.5 W m ⁻¹ K ⁻¹ as noted previously. The values for w , Sv , and α are obtained from the study by Gao and Jelle [1]. The surface roughness factor p obtains values from 0 to 1, where smaller value of p corresponds to a rougher surface and diffusive phonon scattering and larger values correspond to smooth surfaces with specular phonon scattering [1, 32, 44]. Figure 6a shows the thermal conductivities of crystalline nanotubes for different wall thicknesses and scattering factors. The p factor of 0.4 was found best for estimating the thermal conductivity of 2-nm rutile nanoparticles in [57] as well as for silicon nanowires having the diameter of 20–100 nm in [44]. The same p value of 0.4 has also been used for titanate nanotubes by Gao and Jelle [1], who theoretically estimated thermal conductivity values of TNTs between 0.30 and 0.77 W m ⁻¹ K ⁻¹ for 2–3-nm wall thickness. Contrary to the previous reports, by using Eq. 7 our experimental data for TNT_A,T fit with the p factor of 0.26 as shown in Fig. 6a. The practical value is plotted at a maximum wall thickness. For TNT_A , the thermal conductivity value obtained by using Eq. 7 at the maximum wall thickness (12 nm) fits with the calculated surface roughness factor of 0.18. These small values are associated with the rough surface of the anodized nanotubes. The p factor corresponds to p =  1 − 10η / L , where η is the surface roughness of nanotubes and L is the thickness of the material [44]. This equation gives the approximation of surface roughness of 0.22–0.29 nm for TNT_A,T and 0.56–0.96 nm for TNT_A . These values correlate quite well with the roughness values estimated from the TEM micrographs. The difference in surface roughness for both nanotubes results from the synthesis process. It is pointed out that the thermal conductivity increases with increasing wall thickness for both crystalline nanotubes. This provides experimental verification for the model proposed by Liang and Li [44] and modified for nanotubes by Gao and Jelle [1], where thermal conductivity increases with an increase in wall thickness. The decline in the wall dimensions leads to the reduced phonon mean free path by phonon confinement and increased diffuse phonon boundary scattering, resulting in overall reduction in thermal conductivity values [32]. The crystal defects as well should influence the net thermal conductivity value along with the thermal contact resistance between the nanotubes, which are not considered here. Equation 7 is also adapted for the amorphous nanotubes (TNT_Amor ) and the maximum value of wall thickness (30 nm) is plotted in Fig. 6b. The bulk thermal conductivity (κ _B ) of the titania is estimated as 1.6 W m ⁻¹ K ⁻¹ [38] from the minimum thermal conductivity model and l _o is estimated as 0.198 nm [56]. The experimental value fits well with the p factor of 0.65 for amorphous nanotubes, which gives the surface roughness of 0.99–1.98 nm for the TNT_Amor . The mean roughness of TNT_Amor estimated from the TEM images (1.5 nm) fits well with this theoretical range. The surface roughness in one-dimensional crystalline nanostructures (< 100 nm) has a strong impact on the overall thermal conductivity reduction due to the diffusive phonon boundary scattering [58, 59]. In the case of amorphous material, the surface roughness could play a role if it approaches the wavelength of the propagons [36].

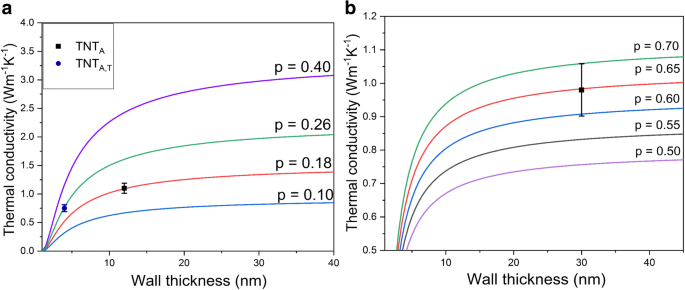
Size-dependent thermal conductivity of a crystalline titania nanotubes (TNT_A and TNT_A,T ) and b amorphous nanotubes (TNT_Amor ) with different surface roughness factors; symbols show the experimental thermal conductivity of the studied titania nanotubes and the solid lines indicate the calculated thermal conductivities by using Eq. 6

Conclusões

Three different kinds of titania nanotubes are synthesized with different crystal structure and morphology by using chemical processing and rapid breakdown anodization methods. Based on the measurement results at room temperature, the thermal conductivity of the titania nanotubes is considerably lower as compared to the bulk titania. Titania (TNT_A ) nanotubes are single-walled with one end opened and other closed, and they have anatase structure and a wall thickness of 7–12 nm. The thermal conductivity of these nanotubes estimated by an effective model of thermal conductivity is 1.07 W m ⁻¹ K ⁻¹ . The amorphous nanotubes (TNT_Amor ) with a wall thickness of 15–30 nm have a thermal conductivity of 0.98 W m ⁻¹ K ⁻¹ . Their thermal conductivity is slightly lower than that of crystalline anatase nanotubes (TNT_A ) However, the multiwalled and open-ended nanotubes (TNT_A,T ) with a mixed crystal structure and a wall thickness of 4–5 nm have the lowest thermal conductivity of 0.75 W m ⁻¹ K ⁻¹ . This low value of thermal conductivity is due to the reduced dimensions of walls approaching the calculated 2.5-nm phonon mean free path. The reduction in the wall thickness is found to result in overall suppression of the thermal conductivity as the phonon confinement is enhanced and the phonon boundary scattering increased. The size confinement effects of phonon transport with different surface-related parameters for both crystalline and amorphous nanotubes are considered. Generally, the thermal conductivity of amorphous oxides is found independent of the size. Comparison of the present result on the amorphous nanotubes with those in the literature, however, suggests also size-dependent reduction in the thermal conductivity of the amorphous nanotubes. This may be due to the possible contribution of propagons in the overall thermal transport in disordered structure along with the diffusons. For TNT_A,T , the thermal conductivity value agrees well with the surface roughness factor of 0.26, while in the case of TNT_A nanotubes, it matches with 0.18 confirming the different surface roughness of the two kinds of crystalline nanotubes related to the synthesis processes. TNT_Amor surface roughness (1.5 nm) estimated from TEM micrographs is in line with the calculated surface roughness factor of 0.65.

Abreviações

RBA:

Rapid breakdown anodization

SEM:

Microscopia eletrônica de varredura

TEM:

Microscopia eletrônica de transmissão

TNT_A :

Titania nanotubes with anatase crystal structure

TNT_A,T :

Titania nanotubes with mixed crystal structure (anatase and titanate)

TNT_Amor :

Titania nanotubes with amorphous structure

TNTs:

Titania nanotubes

XRD:

Difração de raios X

Um estudo da variabilidade na memória de acesso aleatório resistiva de contato por modelo de vacância estocástica Princípios de design para células solares orgânicas aprimoradas com plasma de nanopartículas