Estudos teóricos sobre fotodiodos de avalanche de InGaAs / InAlAs SAGCM

Resumo

Neste artigo, fornecemos uma visão detalhada sobre os fotodiodos de avalanche de absorção, graduação, carga e multiplicação separados InGaAs / InAlAs (SAGCM APDs) e um modelo teórico de APDs é construído. Por meio de análise teórica e simulação bidimensional (2D), a influência da camada de carga e do efeito de tunelamento nos APDs é totalmente compreendida. O desenho da camada de carga (incluindo nível de dopagem e espessura) pode ser calculado por nosso modelo preditivo para diferentes espessuras de multiplicação. Nós descobrimos que conforme a espessura da camada de carga aumenta, a faixa de nível de dopagem adequada na camada de carga diminui. Em comparação com a camada de carga mais fina, o desempenho do APD varia significativamente por meio de vários desvios percentuais das concentrações de dopagem na camada de carga mais espessa. Além disso, a taxa de geração ( G _btt ) do túnel banda a banda é calculado e a influência do efeito de tunelamento no campo de avalanche foi analisada. Confirmamos esse campo de avalanche e fator de multiplicação ( M _n ) na multiplicação diminuirá pelo efeito de túnel. O modelo teórico e a análise são baseados no InGaAs / InAlAs APD; no entanto, eles são aplicáveis a outros sistemas de materiais APD também.

Histórico

Em _0,53 Ga _0,47 Como (doravante referidos como InGaAs), os fotodiodos de avalanche (APDs) são os fotodetectores mais importantes para a detecção de infravermelhos de ondas curtas. Eles são significativos em campos tradicionais, como comunicação por fibra óptica, aplicações de reconhecimento e sensoriamento remoto. InP e In _0,52 Al _0,48 As (doravante referidos como InAlAs) têm o mesmo espaçamento de rede com InGaAs e características de decomposição de grandes avalanches; portanto, eles são os materiais de camada de multiplicação adequados de APDs InGaAs nas aplicações tradicionais. Nos últimos anos, devido ao rápido desenvolvimento da detecção de fóton único na distribuição de chave quântica [1], espectroscopia resolvida no tempo [2], inspeção de circuito VLSI óptico [3] e alcance de laser 3D [4], APDs como a chave componente nessas aplicações têm atraído atenção crescente [5, 6]. Pellegrini et al. descreveram o projeto, fabricação e desempenho de dispositivos InGaAs / InP de geometria plana que foram desenvolvidos para detecção de fóton único com eficiência de detecção de fóton único (SPDE) 10% em 1550 nm (200 K) [7]. Tosi et al. apresentaram os critérios de projeto de um novo fotodiodo de avalanche de fóton único InGaAs / InP (SPAD) com alto SPDE (30%, 225 K), baixo ruído e baixo jitter de temporização [8]. Na simulação, um modelo de dispositivo baseado em dados experimentais foi construído para prever a taxa de contagem de escuridão (DCR) e SPDE de InGaAsP / InP SPADs em [9], e uma plataforma de simulação integrada que pode avaliar o desempenho de distribuição de chave quântica de estado decoy de InGaAs / InP SPADs foi construído em [10]. Acerbi et al. apresentou critérios de projeto para APDs de fóton único InGaAs / InP com um simulador SPAD personalizado [11]. Para os APDs InGaAs / InAlAs, uma estrutura em mesa SPAD InGaAs / InAlAs demonstrou atingir o SPDE de 21% (260 K); entretanto, alta DCR foi observada e foi atribuída à corrente excessiva de tunelamento [12]. Então, [13] usou uma camada espessa de avalanche de InAlAs em APDs de InGaAs / InAlAs para melhorar o SPDE (26%, 210 K) e diminuir o DCR (1 × 10 ⁸ Hz). Na simulação de APDs baseados em InAlAs, um modelo de dispositivo baseado no método de Monte Carlo foi estabelecido para estudar a caracterização básica dos APDs InGaAs / InAlAs em [14], e a influência da camada de carga e da camada de multiplicação na tensão de punção e na quebra. tensão foram estudados com simulações numéricas 2D de estado estacionário em [15].

Em comparação com APDs baseados em InAlAs, as pesquisas de APDs baseados em InP são mais abrangentes e aprofundadas em teoria e simulação. No entanto, o APD baseado em InAlAs é cada vez mais usado no lugar do InP, pois tem um gap maior que pode melhorar as características de quebra tanto nos APDs quanto nos SPADs [16]. A razão do coeficiente de ionização do elétron (α) para o buraco (β) em InAlAs é maior em comparação com InP e, portanto, tem baixo fator de ruído em excesso e produto de alto ganho de largura de banda. Além disso, InAlAs exibe um grande aumento na probabilidade de ruptura com a razão de overbias, fazendo com que os SPADs de InAlAs tenham DCR mais baixo [17]. Algumas propriedades e conclusões importantes sobre os APDs baseados em InAlAs foram obtidas de estudos anteriores, como o baixo excesso de ruído pode ser alcançado em estruturas de InAlAs com regiões de avalanche grossas e finas [18]. O campo elétrico do limiar de tunelamento na absorção (InGaAs) é 1,8 × 10 ⁵ V / cm, e a corrente de tunelamento torna-se o componente dominante da corrente escura no campo alto [14]. Uma estrutura de iluminação vertical tem maior tolerância óptica, mas tem um tradeoff mais sério entre o tempo de trânsito da portadora e a responsividade [19]. Além disso, modelo teórico, estrutura (espessura e dopagem), campo elétrico e outros parâmetros de APD baseados em InAlAs foram estudados em [20,21,22]. No entanto, esses estudos focaram apenas nas influências dos parâmetros comuns da estrutura do APD, como a espessura da camada de absorção, espessura de multiplicação e nível de dopagem da camada de carga. A relação entre os parâmetros de estrutura e o desempenho do APD baseado em InAlAs ainda não foi totalmente compreendida e otimizada.

Neste artigo, um estudo teórico e análise de simulação numérica baseada na estrutura vertical do InGaAs / InAlAs para detecção de comprimento de onda de 1,55 μm foram investigados. Construímos um modelo teórico para estudar a influência dos parâmetros da estrutura no dispositivo e a relação detalhada de cada camada nos APDs. O desenho da camada de carga com diferentes espessuras de multiplicação, a influência da espessura no nível de dopagem na camada de carga e o efeito de tunelamento no campo de avalanche na multiplicação foram analisados e simulados.

Métodos

Nesta seção, uma relação matemática entre os parâmetros do dispositivo e a distribuição do campo elétrico no dispositivo foi construída, a qual foi aplicada para analisar a camada de carga e o efeito de tunelamento. Ao mesmo tempo, um modelo de simulação que incluiu estrutura de simulação, parâmetros de material e modelos físicos básicos foi construído. O modelo de análise teórica e modelo de simulação foi baseado na estrutura vertical do SAGCM InGaAs / InAlAs APD.

Modelo teórico e análise da camada de carga

Parâmetros do dispositivo, como nível de dopagem, espessura, materiais e estrutura, foram usados para construir o modelo matemático para calcular a distribuição do campo elétrico no APD. As teorias físicas básicas que incluem a equação de Poisson, o modelo da camada de depleção e o modelo de junção PN do dispositivo semicondutor podem ser encontradas nos capítulos 1, 2 e 4 em [23] e [24]. A equação do fator de multiplicação da junção pode ser encontrada em [25], e os parâmetros do material semicondutor são de [26]. O modelo apresentado adota a equação de Poisson, a equação da densidade de corrente de tunelamento, o modelo da camada de depleção, o modelo da teoria da junção e o modelo local de ganho de avalanche. O sistema de coordenadas matemáticas simplificado do APD que inclui parâmetros de estrutura básicos (materiais, espessura, dopagem e constante dielétrica) é apresentado na Fig. 1. É uma estrutura SACM APD simplificada que ignora a camada de graduação. Os materiais da camada de contato, camada de carga e camada de multiplicação são InAlAs, e a camada de absorção é InGaAs. As junções de camadas são separadas por X _n , 0, X _m , X _c e X _a e X _p pelo x coordenada. Os níveis de dopagem são expressos por N ₀ , N ₁ , N ₂ , N ₃ , e N ₄ , as espessuras da camada são expressas por w ₀ , w ₁ , w ₂ , w ₃ e w ₄ , e as constantes dielétricas são expressas por ε _s0 , ε _s1 , ε _s2 , ε _s3 e ε _s4 de contato A, multiplicação, carga, absorção e contato B, respectivamente.

O sistema de coordenadas matemáticas simplificado do SACM InGaAs / InAlAs APD. Apresenta as estruturas simplificadas de um APD que é usado para construir um modelo teórico. O sistema de coordenadas matemáticas simplificado do APD que inclui parâmetros de estrutura básicos (materiais, espessura, dopagem e constante dielétrica)

A Equação 1 é a equação de Poisson, que pode resolver a distribuição do potencial elétrico usando a densidade de carga ρ . Nesta equação, ρ é igual a íon dopante N no modelo de camada de depleção, w é igual à espessura da camada de depleção, e ε é a constante dielétrica do material. No modelo comum de distribuição de campo elétrico da junção PN, ρ é uma variável que depende da espessura da camada de depleção w e íon dopante N . Neste modelo, ele muda depois de considerar o efeito de tunelamento. No entanto, antes de considerar o efeito de tunelamento, primeiro construímos a distribuição do campo elétrico usando um método comum.
$$ \ frac {d \ xi} {d x} =\ frac {\ rho} {\ varejpsilon} =\ frac {q \ times N} {\ varejpsilon} $$ (1)
Resolvendo a equação de Poisson com os parâmetros do dispositivo, a expressão matemática do campo elétrico máximo é obtida. Esta expressão é determinada pela variação da espessura de penetração na camada de depleção mostrada nas Fórmulas 2 e 3. Nesta expressão, os parâmetros que incluem os níveis de dopagem ( N ), espessuras da camada de depleção ( w ), e constantes dielétricas ( ε) de diferentes camadas podem ser encontradas na Fig. 1.
$$ {\ xi} _ {\ max (w)} ={\ sum} _ {k =1} ^ 4 \ left (- \ frac {q \ times {N} _k \ times {w} _k} {\ Varepsilon_ {sk}} \ right) $$ (2) $$ {\ xi} _ {\ max (w)} =\ frac {q \ times {N} _0 \ times {w} _0} {\ varejpsilon_ {s0 }} $$ (3)
Então, a distribuição do campo elétrico pode ser derivada em todos os pontos usando as Fórmulas 4 e 5. A condição de contorno ignora o potencial embutido V _br na Fórmula 6; portanto, a relação matemática entre a espessura da camada de depleção e a tensão de polarização pode ser calculada.
$$ {\ xi} _ {\ left (x, w \ right)} ={\ xi} _ {\ max (w)} + {\ sum} _ {k =1} ^ 4 \ left (\ frac { q \ times {N} _k \ times \ left | x \ right |} {\ varejpsilon_ {sk}} \ right) \ left ({X} _p Finalmente, a relação matemática entre a distribuição do campo elétrico e a tensão de polarização no dispositivo é obtida usando as Fórmulas 7-11:
$$ \ xi \ left (x, {V} _ {\ mathrm {bias}} \ right) ={\ xi} _ {\ max \ left ({V} _ {\ mathrm {bias}} \ right)} + \ frac {q \ times {N} _1 \ times \ left | x \ right |} {\ varejpsilon_ {s1}} \ left (0 \ ge x \ ge {X} _m \ right) $$ (7) $ $ \ xi \ left (x, {V} _ {\ mathrm {bias}} \ right) ={\ xi} _ {\ max \ left ({V} _ {\ mathrm {bias}} \ right)} + \ frac {q \ times {N} _1 \ times {w} _1} {\ varepsilon_ {s1}} + \ frac {q \ times {N} _2 \ times \ left | x- {X} _m \ right |} {\ varejpsilon_ {s2}} \ left ({X} _m \ ge x \ ge {X} _c \ right) $$ (8) $$ \ xi \ left (x, {V} _ {\ mathrm {bias} } \ right) ={\ xi} _ {\ max \ left ({V} _ {\ mathrm {bias}} \ right)} + \ frac {q \ times {N} _1 \ times {w} _1} { \ varejpsilon_ {s1}} + \ frac {q \ times {N} _2 \ times {w} _2} {\ varejpsilon_ {s2}} + \ frac {q \ times {N} _3 \ times \ left | x- { X} _c \ right |} {\ varepsilon_ {s3}} \ left ({X} _c \ ge x \ ge {X} _a \ right) $$ (9) $$ \ xi \ left (x, {V} _ {\ mathrm {bias}} \ right) ={\ xi} _ {\ max \ left ({V} _ {\ mathrm {bias}} \ right)} + \ frac {q \ times {N} _1 \ vezes {w} _1} {\ varepsilon_ {s1}} + \ frac {q \ times {N} _2 \ times {w} _2} {\ varepsilon_ {s2}} + \ frac {q \ times {N} _3 \ vezes {w} _3} {\ varepsilon_ {s3}} + \ frac {q \ times {N} _4 \ times \ left | x- {X} _a \ right |} {\ varepsilon_ {s4}} \ left ({X} _a \ ge x \ ge {X} _p \ right) $$ (10) $$ \ xi \ left (x, {V} _ { \ mathrm {bias}} \ right) ={\ xi} _ {\ max \ left ({V} _ {\ mathrm {bias}} \ right)} - \ frac {q \ times {N} _0 \ times x } {\ varepsilon_ {s0}} \ left (0 \ le x \ le {X} _n \ right) $$ (11)
A partir do modelo, uma vez que o limite da camada de depleção atinge a região de contato, as Fórmulas 7-11 podem ser usadas para analisar o campo elétrico em cada camada. No APD prático, as camadas de absorção e multiplicação são dopadas involuntariamente em camadas intrínsecas. N ₃ e N ₁ são menores que N ₂ . Assim, a Fórmula 9 é aproximadamente igual à Fórmula 12. É a razão pela qual a camada de carga pode controlar a distribuição do campo elétrico no dispositivo.
$$ {\ displaystyle \ begin {array} {l} \ xi \ left (x, {V} _ {\ mathrm {bias}} \ right) ={\ xi} _ {\ max \ left ({V} _ {\ mathrm {bias}} \ right)} + \ frac {q \ times {N} _1 \ times {w} _1} {\ varepsilon_ {s1}} + \ frac {q \ times {N} _2 \ times { w} _2} {\ varepsilon_ {s2}} + \ frac {q \ times {N} _3 \ times \ left | x- {X} _c \ right |} {\ varepsilon_ {s3}} \\ {} \ kern4em \ approx {\ xi} _ {\ max \ left ({V} _ {\ mathrm {bias}} \ right)} + \ frac {q \ times {N} _2 \ times {w} _2} {\ varejpsilon_ { s2}} \ left ({X} _ {\ mathrm {c}} \ ge x \ ge {X} _a \ right) \ end {array}} $$ (12)
Na Fórmula 8, a diferença do campo elétrico entre a multiplicação e a absorção é determinada usando o produto de N ₂ e w ₂ . N ₂ é o nível de dopagem na camada de carga e w ₂ é a espessura da camada de carga. Para uma distribuição de campo elétrico adequada no InGaAs / InAlAs APD, o campo elétrico na camada de absorção (InGaAs) deve estar dentro dos valores de intervalo de 50-180 kV / cm que garantem velocidade suficiente para os portadores fotoinduzidos e evitam o efeito de túnel na camada de absorção [10]. Ou seja, o campo de avalanche na multiplicação deve diminuir para 50-180 kV / cm na absorção pela camada de carga. Assim, podemos usar a Fórmula 8 para encontrar o nível de dopagem calculado ideal e espessuras da camada de carga. Quando a camada de multiplicação é de 200 nm (o campo de avalanche E na multiplicação é 6,7 × 10 ⁵ V / cm enquanto a camada de multiplicação é de 200 nm [27]); os valores calculados do nível de dopagem e espessura na camada de carga são comparados com os resultados de [28,29,30,31,32,33] na Fig. 2. A região dos valores teóricos está de acordo com os dados experimentais. Este resultado prova que a Fórmula 8 pode ser usada para prever o nível de dopagem com diferentes espessuras na camada de carga quando a espessura de multiplicação é certa.

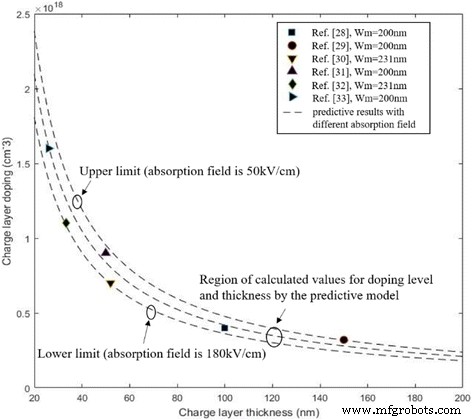
Comparação de resultados teóricos e dados de experimentos de vários relatórios ( w _m =200 nm). Símbolos fechados:o nível de dopagem e a espessura da camada de carga com espessura de multiplicação de 200 nm (quadrado preto, círculo preto, triângulo preto, triângulo preto apontando para a direita) e 231 nm (diamante preto, triângulo preto apontando para baixo) nas referências. Apresenta os valores calculados da camada de carga (nível de dopagem e espessura) pela Fórmula 8 (o campo de absorção é 50-180 kV / cm). Quando o campo de absorção é de 50 kV / cm, o limite superior do nível de dopagem na camada de carga pode ser obtido. Quando o campo de absorção é de 180 kV / cm, o limite inferior do nível de dopagem na camada de carga pode ser obtido. Comparamos os resultados teóricos e os dados experimentais de vários relatórios. A região dos valores teóricos está de acordo com os dados experimentais. Linhas tracejadas os valores calculados de nível de dopagem e espessura pela fórmula

Calculamos o nível de dopagem ideal para diferentes espessuras da camada de carga com a camada de multiplicação de 300, 500 e 700 nm, e os resultados são apresentados na Fig. 3. Este resultado ilustra que a tolerância no nível de dopagem na camada de carga é relacionado à sua espessura e a faixa de nível de dopagem diminui com o aumento da espessura da camada de carga. Ou seja, se aplicarmos uma região de carga espessa, apenas uma pequena faixa de nível de dopagem na camada de carga existiria para satisfazer o campo elétrico ideal. Como resultado, o desempenho do APD varia significativamente por meio de vários desvios percentuais das concentrações de dopagem na camada de carga mais espessa. Na seção "Resultados e Discussão", as estruturas práticas dos APDs foram simuladas para estudar e verificar a análise teórica, que inclui a influência da espessura da camada de carga na faixa de nível de dopagem na camada de carga e a variedade de desempenho para diferentes espessuras da camada de carga em APDs.

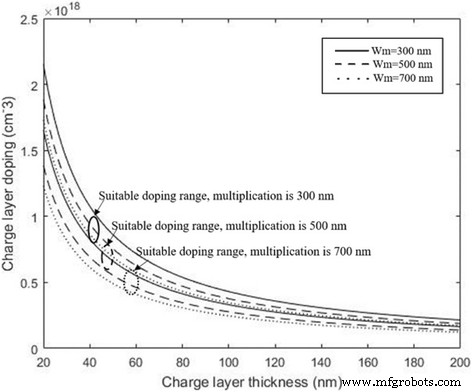
O nível ideal de dopagem e a espessura da camada de carga para as diferentes camadas de multiplicação. Linha sólida: w _m =300 nm. Linha tracejada: w _m =500 nm. Linha pontilhada: w _m =700 nm. Apresenta os valores calculados da camada de carga (nível de dopagem e espessura) pela fórmula, enquanto o campo da camada de absorção é adequado. As espessuras da camada de multiplicação são 300, 500 e 700 nm. Quando a espessura da camada de multiplicação é certa, podemos usar a fórmula para encontrar o nível de dopagem ideal e a espessura da camada de carga

Modelo teórico com consideração de encapsulamento

O modelo de análise acima é sobre a distribuição do campo elétrico no dispositivo e baseado na premissa de que ρ é o íon dopante na camada de depleção. Se um campo elétrico suficientemente alto existe dentro da camada de absorção, a curvatura da banda local pode ser suficiente para permitir que os elétrons entrem no túnel [34]. Portanto, o tunelamento de elétrons pode ocorrer. A partir do diagrama esquemático de tunelamento na Fig. 4, quando a camada de absorção tem um tunelamento de ruptura, o efeito de tunelamento altera a densidade de carga ρ , a carga positiva na absorção aumenta e a carga negativa nas camadas de multiplicação e carga aumenta. Assim, ρ não é igual à densidade de carga de íon dopante na camada de depleção enquanto o efeito de tunelamento aparece. As fórmulas que foram discutidas anteriormente serão alteradas após considerar o efeito de tunelamento.

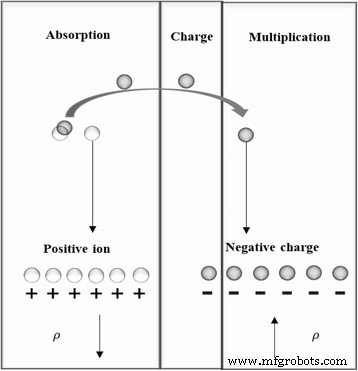
Processo de tunelamento e alteração da densidade de carga nas camadas de multiplicação e absorção. Apresenta um diagrama esquemático do processo de tunelamento no dispositivo. Se um campo elétrico suficientemente alto existe dentro da camada de absorção, a curvatura da banda local pode ser suficiente para permitir que os elétrons entrem no túnel. Quando a camada de absorção tem um tunelamento de rompimento, a carga positiva na absorção aumenta e a carga negativa nas camadas de multiplicação e carga aumenta. Assim, ρ não é igual à densidade de carga de íon dopante na camada de depleção enquanto o efeito de tunelamento aparece

A taxa de geração G _bbt do túnel banda a banda é descrito na Fórmula 13 [35, 36].
$$ {G} _ {bbt} ={\ left (\ frac {2 {m} ^ {\ ast}} {E_g} \ right)} ^ {1/2} \ frac {q ^ 2 {E_p} ^ {\ gamma}} {{\ left (2 \ pi \ right)} ^ 3 {\ hbar} ^ 2} \ exp \ left (\ frac {- \ pi} {4 {q \ mathit {\ hbar E}} _p} {\ left (2 {m} ^ {\ ast} \ times {E_g} ^ 3 \ right)} ^ {\ raisebox {1ex} {$ 1 $} \! \ left / \! \ raisebox {-1ex} {$ 2 $} \ right.} \ Right) =A \ times {E_p} ^ {\ gamma} \ times \ exp \ left (- \ frac {B} {E_p} \ right) $$ (13)
Na Fórmula 13, E _g é a diferença de banda de energia de InGaAs, m * (igual a 0,04 m _e ) é a massa reduzida efetiva, E _p é o campo elétrico de ruptura na camada de absorção, e γ é um parâmetro definido pelo usuário, geralmente restrito a 1 ~ 2. O A e B são os parâmetros de caracterização. Calculamos o G _bbt com γ diferente , e os resultados são mostrados na Fig. 5. Pode-se verificar que G _bbt adapta a mesma ordem de magnitude para o nível de dopagem da camada de carga enquanto γ é restrito a 1 ~ 1,5.

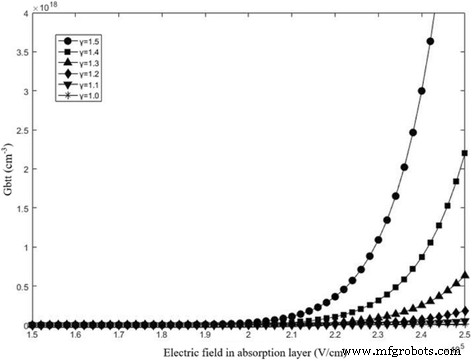
O G _btt para diferentes campos na camada de absorção com diferentes γ . Os valores de γ é 1,0 (estrela preta), 1,1 (triângulo preto apontando para baixo), 1,2 (losango preto), 1,3 (triângulo preto), 1,4 (quadrado preto), 1,5 (círculo preto). Apresenta os resultados calculados de G _btt pela Fórmula 13. Quando o campo de absorção excede 19 kV / cm, G _bbt aumenta gradualmente. Também pode ser verificado que G _bbt adapta a mesma ordem de magnitude para o nível de dopagem da camada de carga enquanto γ é restrito a 1 ~ 1,5

Como resultado, a densidade de carga ρ é uma variável e determinada pelo efeito de tunelamento e o íon dopante no túnel de absorção. Nesta ocasião, a Fórmula 1 será alterada para Fórmula 14 e o campo elétrico na camada de multiplicação será descrito pela Fórmula 15. w _túnel é a camada de depleção efetiva do processo de tunelamento [35]. Assim, a mudança do campo de avalanche pode ser descrita pela Fórmula 16, e o campo de avalanche diminuirá na multiplicação com o efeito de tunelamento.
$$ \ frac {d \ xi} {dx} =\ frac {\ rho} {\ varepsilon} =\ frac {q \ times \ left (N + {G} _ {btt} \ right)} {\ varejpsilon}, {E} _p> 1,8 \ vezes {10} ^ 5V / cm $$ (14) $$ \ xi \ left (x, {V} _ {\ mathrm {bias}} \ right) ={\ xi} _ { \ max \ left ({V} _ {\ mathrm {bias}} \ right)} + \ frac {q \ times \ left ({N} _1 \ times \ left | x \ right | + {G} _ {bbt } \ times {w} _ {\ mathrm {túnel}} \ right)} {\ varepsilon_ {s1}} \ left (0 \ ge x \ ge {X} _m \ right) $$ (15) $$ \ delta \ xi \ left (x, {V} _ {\ mathrm {bias}} \ right) =\ delta E =\ frac {q \ times {G} _ {btt} \ times {w} _ {\ mathrm {túnel }}} {\ varepsilon _ {\ mathrm {s} 3}} $$ (16)
Os coeficientes de ionização de elétrons e orifícios são descritos pelas Fórmulas 17 e 18 em [18]. E é o campo de avalanche em multiplicação.
$$ \ alpha ={a} _n {e} ^ {\ raisebox {1ex} {$ - {b} _n $} \! \ left / \! \ raisebox {-1ex} {$ E $} \ right.} $$ (17) $$ \ beta ={a} _p {e} ^ {\ raisebox {1ex} {$ - {b} _p $} \! \ Left / \! \ Raisebox {-1ex} {$ E $ } \ certo.} $$ (18)
O efeito da avalanche de portadores é contabilizado pelo modelo de ionização por impacto. Considerando a densidade de portadores extremamente baixa da camada de multiplicação em comparação com a camada de carga, é razoável supor que o campo elétrico é uniforme em toda a camada de multiplicação. Portanto, o fator de multiplicação ( M _n ) pode ser expressa como a seguinte Eq. 19. Aqui, w _m é a espessura da camada de multiplicação e k é a razão do coeficiente de ionização de impacto definido por α / β . Desde k varia muito lentamente com o campo elétrico, k é aproximadamente constante para uma ligeira variação de w _m [37].
$$ {M} _n =\ frac {k-1} {k \ times {e} ^ {- \ alpha \ left (1- \ raisebox {1ex} {$ 1 $} \! \ Left / \! \ Raisebox { -1ex} {$ k $} \ right. \ Right) {w} _m} -1} $$ (19)
Assumindo constante w _m e tensão de polarização, diferenciação de M _n com relação aos coeficientes de ionização de elétrons está nas Fórmulas 20 e 21.
$$ \ delta {M} _n \ left | {} _ {w =const \ &V =const} \ right. ={M_n} ^ 2 {e} ^ {- \ alpha \ left (1- \ raisebox {1ex} {$ 1 $} \! \ Left / \! \ Raisebox {-1ex} {$ k $} \ right. \ Right) {w} _m} \ times {w} _m \ delta \ alpha $$ (20) $$ \ delta \ alpha =\ frac {\ delta \ alpha} {\ delta E} ={\ alpha} _n {b} _n {e} ^ {\ frac {- {b} _n} {E}} \ frac {1 } {E ^ 2} $$ (21)
Nas Fórmulas 20 e 21, δα / δE é positivo. Supõe-se que 20% de uma camada de absorção de depleção total é w _túnel e a camada de absorção tem 400 nm de espessura. Ao resolver a Fórmula 16, a relação entre o δE e o campo de absorção com diferentes γ é apresentado na Fig. 6. Pode-se verificar que δE adapta a mesma ordem de magnitude para o campo de avalanche na multiplicação. Assim, o efeito de tunelamento tem influência sobre o campo de avalanches e o M _n diminuirá com o efeito de tunelamento. Na análise, assumimos que a carga negativa não é multiplicada na multiplicação e o modelo ficará mais rigoroso depois de levado em consideração. Para verificar e analisar a influência do efeito de tunelamento na estrutura prática dos APDs, simulamos a relação entre o efeito de tunelamento e o campo de avalanche de multiplicação em detalhes na seção “Resultados e Discussão”.

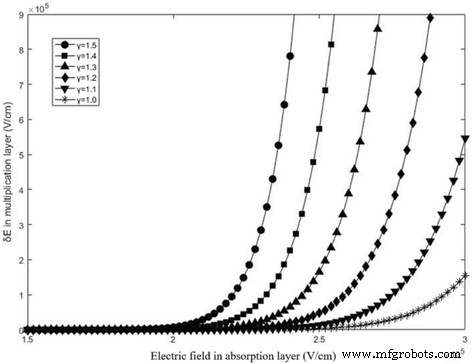
O δE para diferentes campos na camada de absorção com diferentes γ . Os valores de γ é 1,0 (estrela preta), 1,1 (triângulo preto apontando para baixo), 1,2 (losango preto), 1,3 (triângulo preto), 1,4 (quadrado preto), 1,5 (círculo preto). Apresenta os resultados calculados de δE pela Fórmula 16. Quando o campo de absorção excede 19 kV / cm, δE aumenta gradualmente. Também pode ser verificado que δE adapta a mesma ordem de magnitude para o campo de avalanche na multiplicação. Assim, o efeito de tunelamento tem influência no campo de avalanche com o efeito de tunelamento

Estrutura e modelo de simulação

Uma simulação de dispositivo semicondutor de TCAD foi usada para simulação e análise. Este motor de simulação define modelos físicos na simulação, e os resultados têm um significado físico [20]. Os modelos físicos básicos foram apresentados a seguir. Os modelos de deriva-difusão, incluindo as equações de Poisson e de continuidade da portadora, foram usados para simular a distribuição do campo elétrico e a corrente de difusão I _DIFF . O modelo de tunelamento banda a banda foi usado para a corrente de tunelamento banda a banda I _B2B , e o modelo de tunelamento assistido por armadilha foi usado para a corrente de tunelamento assistida por armadilha I _TAT . A corrente de geração-recombinação I _GR foi descrito pelo modelo de recombinação Shockley – Read – Hall e a recombinação Auger atual I _AUGER foi descrito pelo modelo de recombinação Auger. A corrente escura foi descrita claramente por esses mecanismos [38]. A multiplicação da avalanche foi descrita pelo modelo de ionização por impacto Selberherr. Outros modelos básicos, incluindo as estatísticas de portadores Fermi-Dirac, dependentes da concentração de portadores, baixa mobilidade de campo, saturação de velocidade e métodos de rastreamento de raios, foram usados para o modelo de simulação, e um modelo de simulação rigoroso foi construído.

As estruturas do dispositivo na simulação foram semelhantes às estruturas experimentais em [13]. A seção transversal esquemática do APD SAGCM InGaAs / InAlAs iluminado pela parte superior é mostrada na Fig. 7. As estruturas de cima para baixo são sequencialmente denominadas como camada de contato InGaAs, camada de revestimento InAlAs, camada de classificação InAlGaAs, camada de absorção InGaAs, classificação InAlGaAs camada, camada de carga InAlAs, camada de multiplicação InAlAs, camada de revestimento InAlAs, camada de contato InP e substrato InP. A espessura e a dopagem de cada camada também são apresentadas na Fig. 7. Para evitar a influência da espessura nos resultados da simulação, escolhemos duas estruturas de simulação. Uma estrutura de simulação é chamada de APD-1 (as camadas de multiplicação e absorção são de 800 e 1800 nm, respectivamente), e a outra estrutura de simulação é chamada de APD-2 (as camadas de multiplicação e absorção são de 200 e 600 nm, respectivamente).

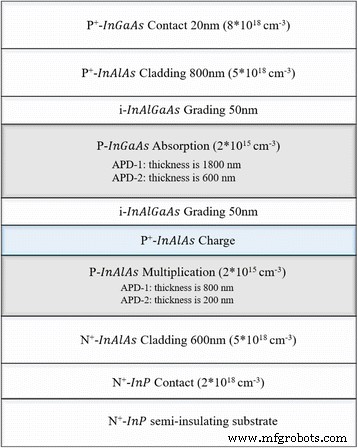
Estrutura de simulação e parâmetros do APD. Apresenta a seção transversal esquemática do SAGCM InGaAs / InAlAs APD-1 e APD-2 com iluminação superior. Inclui estrutura, materiais, dopagem e espessura

Para testar o modelo de simulação, os dados do experimento em [13] foram comparados com os resultados da simulação. Nesta simulação, usamos a mesma estrutura na referência, e as características corrente-tensão do dispositivo foram fornecidas. A Figura 8 mostra nossos resultados de simulação e os resultados do experimento na referência. Eles têm a tensão de passagem semelhante V _pt e tensão de ruptura V _br . Além disso, os resultados da simulação e do experimento correspondem bem. Portanto, o modelo em nossa simulação é preciso. Os parâmetros mencionados acima estão listados na Tabela 1.

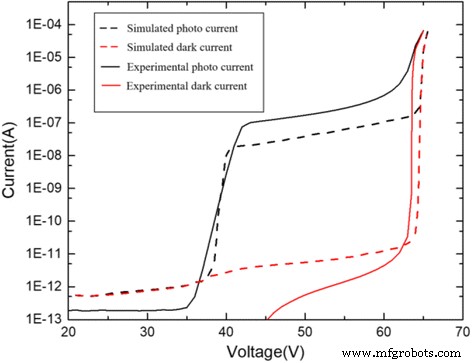
Resultados da simulação comparados com os resultados do experimento (fotocorrente e corrente escura). Linha tracejada preta:foto atual simulada. Linha tracejada vermelha:corrente escura simulada. Linha sólida preta:foto atual experimental. Linha contínua vermelha:corrente escura experimental. Apresenta a comparação dos resultados da simulação e dos resultados do experimento. O modelo de simulação usa os mesmos parâmetros do experimento na referência

Resultados e discussão

Nesta seção, a análise teórica e as conclusões foram estudadas por simulação em detalhes. Primeiro, a influência da espessura da camada de carga na tolerância do nível de dopagem na camada de carga foi estudada na seção “Influência da espessura da camada de carga”. Em seguida, a relação entre o efeito de túnel e o campo de multiplicação da avalanche foi analisada e verificada na seção “Efeito de túnel na distribuição do campo elétrico”.

Influência da espessura da camada de carga

De [14], uma distribuição de campo adequada no InGaAs / InAlAs APD deve cumprir essas regras. A garantia V _pt < V _br e V _br - V _pt deve ter uma margem de segurança para variações de processamento em flutuações de temperatura e faixa de operação. Na camada de absorção, o campo elétrico deve ser maior que 50–100 kV / cm para garantir velocidade suficiente para os portadores fotoinduzidos. Ao mesmo tempo, o campo elétrico deve ser inferior a 180 kV / cm para evitar o efeito de tunelamento na camada de absorção. A distribuição do campo elétrico influencia muito o desempenho do dispositivo. A escolha do campo elétrico na camada de absorção equilibra o equilíbrio entre o pequeno tempo de trânsito, a corrente escura e a alta responsividade para os requisitos práticos.

In the simulation, we used the structure of APD-1 (multiplication is 800 nm thick) and adjusted the charge layer thickness from 50 to 210 nm to study the influence of charge layer thickness on doping level range and verify the theoretical conclusions in analytical model. In the simulation, we selected different doping level ranges in the charge layer so that the electric field distribution complies with the rules. The simulation results on the relationship between thickness and doping level range in the charge layer are presented in Fig. 9a. As the charge layer thickness increases, the suitable doping level range in charge layer decreases. A relatively large doping level range exists in the thin charge layer, and under this doping level range, the device will have a suitable electric field distribution. Apparently, the doping level range is determined by charge layer thickness. The simulation result of APD-2 (with a thickness of multiplication of 200 nm) is presented in Fig. 9b, which has a similar result. Moreover, it can be found that the calculated results of Fig. 2 and simulation results of Fig. 9b match well as shown in Fig. 9c. The small difference between the calculated results and simulation results is caused by the different values of avalanche field in the simulation and calculation. The avalanche field in simulation engine is used 6.4 × 10⁵ V/cm, while in the calculation, we use the value of 6.7 × 10⁵ V/cm from [27].

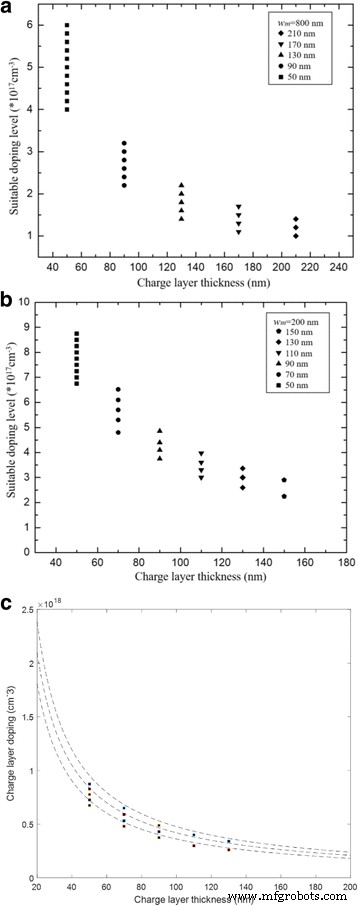
a Relationship between suitable doping level and thickness of charge layer (APD-1). The thickness of charge layer is 50 nm (black square), 90 nm (black circle), 130 nm (black triangle), 170 nm (black down-pointing triangle), 210 nm (black diamond). a presents the suitable doping level region for different thickness of charge layer. As the charge layer thickness increases, the suitable doping level range in the charge layer decreases. A relatively large doping level range exists in the thin charge layer, and under this doping level range, the device will have a suitable electric field distribution. Apparently, the doping level range is determined by charge layer thickness. b Relationship between suitable doping level and thickness of charge layer (APD-2). The thickness of charge layer is 50 nm (black square), 70 nm (black circle), 90 nm (black triangle), 110 nm (black down-pointing triangle), 130 nm (black diamond), and 150 nm (black pentagon). The figure description of b is similar to a . c Comparison of calculated results in Fig. 2 and simulated results in Fig. 9b. Dashed line:calculated results. Closed symbols:simulated results (black square). c presents the comparison of calculated results in Fig. 2 and simulated results in Fig. 9b. The calculated results and simulated results correspond well

The charge layer thicknesses of 210 and 50 nm (APD-1) were selected to show the simulation details and the influence of doping level on the electric field distribution. Figure 10a, c shows the current simulation results of different doping levels in thicknesses of 210 and 50 nm, respectively. Figure 10b, d shows the electric field distribution simulation results using the same structure. The simulation results show that thicknesses of 210 and 50 nm have doping level ranges of 1.0 × 10¹⁷ –1.3 × 10¹⁷ cm ⁻³ and 3.9 × 10¹⁷ –5.7 × 10¹⁷ cm ⁻³ , respectivamente.

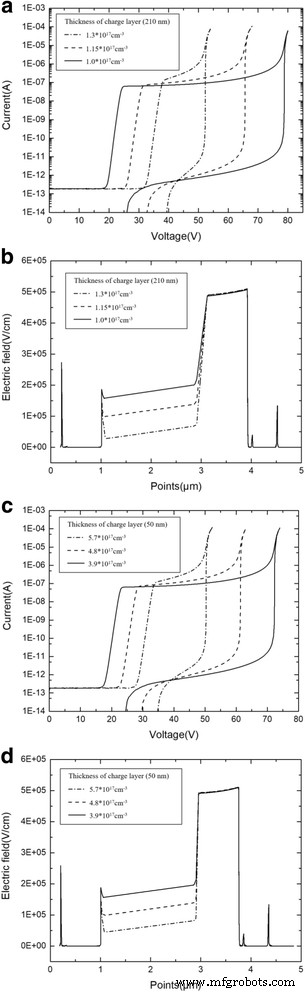
a Photocurrent and dark current with different doping level (thickness of charge layer is 210 nm). Solid line:doping level in the charge layer is 1.3 × 10¹⁷ cm ⁻³ . Dashed line:doping level in charge layer is 1.15 × 10¹⁷ cm ⁻³ . Dashed dot line:doping level in charge layer is 1.0 × 10¹⁷ cm ⁻³ . a Presents the simulation results of currents with different doping level. The device with a charge layer thickness of 210 nm only has a relatively narrow and suitable doping level. A minimal change in the doping level has greatly influence the punch-through voltage, breakdown voltage, and current-voltage characteristic. b Avalanche field with different doping level (thickness of charge layer is 210 nm). Solid line:doping level in charge layer is 1.3 × 10¹⁷ cm ⁻³ . Dashed line:doping level in charge layer is 1.15 × 10¹⁷ cm ⁻³ . Dashed dot line:doping level in charge layer is 1.0 × 10¹⁷ cm ⁻³ . b Presents the simulation results of fields with different doping level. The device with a charge layer thickness of 210 nm only has a relatively narrow and suitable doping level. A minimal change in the doping level has greatly influenced the electric field distribution. c Photocurrent and dark current with different doping level (thickness of charge layer is 50 nm). Solid line:doping level in charge layer is 5.7 × 10¹⁷ cm ⁻³ . Dashed line:doping level in charge layer is 4.8 × 10¹⁷ cm ⁻³ . Dashed dot line:doping level in charge layer is 3.9 × 10¹⁷ cm ⁻³ . c Presents the simulation results of currents with different doping level. The device with a charge layer thickness of 50 nm has a relatively wide and suitable doping level. A minimal change in the doping level has a small influence on the current-voltage characteristic. d Avalanche field with different doping level (thickness of charge layer is 50 nm). Solid line:doping level in charge layer is 5.7 × 10¹⁷ cm ⁻³ . Dashed line:doping level in charge layer is 4.8 × 10¹⁷ cm ⁻³ . Dashed dot line:doping level in charge layer is 3.9 × 10¹⁷ cm ⁻³ . d Presents the simulation results of fields with different doping level. The device with a charge layer thickness of 50 nm only has a relatively wide and suitable doping level. A minimal change in the doping level has a small influence on the electric field distribution

Clearly, the device with a charge layer thickness of 210 nm only has a relatively narrow and suitable doping level. A minimal change in the doping level has greatly influence the current-voltage characteristic and electric field distribution. As a result, the performance of APD varies significantly via several percent deviations of doping concentrations in the thicker charge layer. This conclusion is the same as the theoretical analysis. Concurrently, when designing APD structures, choosing a thin charge layer will give a high level of doping tolerance, as well as confer APD with good controllability.

Finally, the relationship between charge layer and multiplication thickness was simulated. Figure 11a presents the avalanche field with multiplication region thicknesses of 100, 200, and 300 nm in the APD-2 structure (with a charge layer thickness of 70 nm). Figure 11b presents the charge layer doping range with different multiplication thicknesses at the suitable electric field distribution condition. The charge layer thicknesses are 50, 70, and 90 nm. Clearly, a high avalanche field exists in the thin multiplication layer. As the multiplication region thickness decreases, the electric field difference between multiplication and absorption layers increases. As a result, a thin multiplication layer needs a high product of the charge layer doping level and thickness to reduce the high avalanche field.

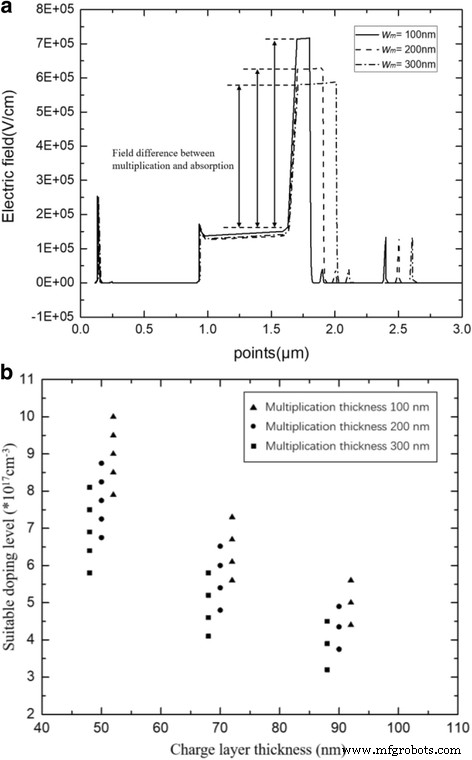
a Avalanche breakdown electric field with different multiplication thicknesses. Solid line:w _m = 100 nm. Dashed line:w _m = 200 nm. Dashed dot line:w _m = 300 nm. a Presents the simulation results of electric field distribution with different w _m . As the w _m decreases, the avalanche field in the multiplication increase. b Relationship between multiplication thickness and charge layer. The thickness of multiplication is 300 nm (black square), 200 nm (black circle), 100 nm (black triangle). b Presents the relationship between multiplication thickness and charge layer. A thin multiplication layer needs a high product of the charge layer doping level and thickness to reduce the high avalanche field

Tunneling Effect on the Electric Field Distribution

The simulation in this part will study the tunneling effect on the electric field in the device. From the theoretical analysis, the tunneling effect has an influence on the avalanche field in multiplication. Thus, the simulation will design to study the influence of electric field in the absorption layer that exceeds the tunneling threshold value. First, group A, with the structure of APD-1, charge layer thickness of 90 nm, and different charge layer doping levels of 1.4 × 10¹⁷ –2.4 × 10¹⁷ cm ⁻³ , was simulated for electric field distribution when the device avalanche breaks down. The result is shown in Fig. 12a. When the charge layer doping level exceeds 2.0 × 10¹⁷ cm ⁻³ , the field in the absorption layer becomes lower than the tunneling threshold field and the avalanche field in the multiplication layer reaches the same value. However, when the doping level is less than 2.0 × 10¹⁷ cm ⁻³ , the field in the absorption layer exceeds the tunneling threshold field and the avalanche field in the multiplication layer decreases with the decrease of the doping level in charge layer. Similar results were observed in the APD-2 structure (with a charge layer thickness of 90 nm and doping level of 2.2 × 10¹⁷ –3.6*10¹⁷ cm ⁻³ ) (Fig. 12b). That is, if the electric field in the absorption layer exceeds the tunneling threshold value at or over the breakdown voltage, then the breakdown electric field in the multiplication will decrease.

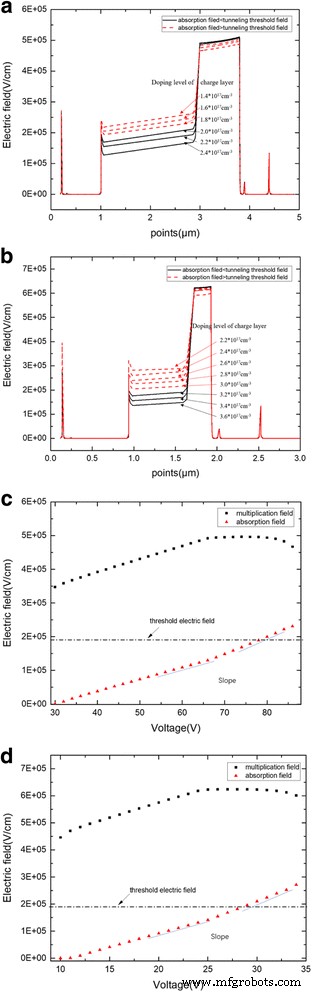
a Avalanche breakdown electric field with different doping levels (APD-1). Thickness of charge layer is 90 nm. Red dashed lines:the field of absorption is larger than the tunneling threshold field. Black solid lines:the field of absorption is less than the tunneling threshold field. a Presents the simulation results of electric field distribution with different doping level while avalanche breakdown. When doping level of charge layer exceeds 2.0 × 10¹⁷ cm ⁻³ , the field in the absorption layer becomes lower than the tunneling threshold field, and the avalanche field in the multiplication layer reaches the same value with different doping level. However, when the doping level is less than 2.0 × 10¹⁷ cm ⁻³ , the field in the absorption layer exceeds the tunneling threshold field, and the avalanche field in the multiplication layer decreases with the decrease of the doping level. Thus, if the electric field in the absorption layer exceeds the tunneling threshold value at or over the breakdown voltage, then the breakdown electric field in the multiplication will decrease. Thus, the electric field in the absorption should be less than the tunneling threshold value to maintain the high field in the multiplication layer when the device avalanche breaks down. b Avalanche breakdown electric field with different doping levels (APD-2). Thickness of charge layer is 90 nm. Red dashed lines:the field of absorption is larger than the tunneling threshold field. Black solid lines:the field of absorption is less than the tunneling threshold field. The figure description of b is similar to a . c Relationship between field and bias voltage in multiplication and absorption (APD-1). Thickness of charge layer is 90 nm. Electric field of multiplication (black square). Electric field of absorption (red triangle). c Presents the relationship between the electric field and bias voltage in multiplication and absorption layers. When the electric field in the absorption layer reaches the tunneling threshold value, the avalanche breakdown electric field in the multiplication gradually decreases. Moreover, the absorption field slope increases when the electric field in the absorption layer exceeds the tunneling threshold. d Relationship between field and bias voltage in multiplication and absorption (APD-2). Thickness of charge layer is 90 nm. Electric field of multiplication (black square). Electric field of absorption (red triangle). The figure legend of d is similar to a

Groups B (APD-1 thickness of 90 nm, doping level of 2.4 × 10¹⁷ cm ⁻³ in charge layer and APD-2 thickness of 90 nm, doping level of 3.6 × 10¹⁷ cm ⁻³ ) were designed to demonstrate the relationship between the threshold electric field in the absorption layer and avalanche field in the multiplication layer. The multiplication and absorption electric fields vary with the bias voltage on the device. As shown in Fig. 12c, d, when the electric field in the absorption layer reaches the tunneling threshold value, the avalanche breakdown electric field in the multiplication gradually decreases. Moreover, when the absorption field exceeds the tunneling threshold, the avalanche breakdown electric field in the multiplication layer plummets. Furthermore, the absorption field slope increases when the electric field in the absorption layer exceeds the tunneling threshold.

The phenomenon in Fig. 12 can be explained by the theoretical analysis that tunneling has an influence on the charge density in the “Methods” section. When the electric field reaches the tunneling threshold value in the absorption layer, the charge density ρ becomes unequal to the dopant ion. The multiplication field will decrease as the negative ion increases, and the absorption field will increase as the positive ion increases. Concurrently, the absorption field slope will increase due to the tunneling effect. As a result, the electric field in the absorption should be less than the tunneling threshold value to maintain the high field in the multiplication layer and the low dark current when the device avalanche breaks down.

Conclusões

In summary, we have presented a theoretical study and numerical simulation analysis involving the InGaAs/InAlAs APD. The mathematical relationship between the device parameters and electric field distribution in the device was built. And the tunneling effect was taken into consideration in the theoretical analysis. Through analysis and simulation, the influence of structure parameters on the device and the detailed relationship of each layer were fully understood in the device. Three important conclusions can be obtained from this paper. First, the doping level and thickness of the charge layer for different multiplication thicknesses can be calculated by the theoretical model in the “Methods” section. Calculated charge layer values (doping and thickness) are in agreement with the experiment results. Second, as the charge layer thickness increases, the suitable doping level range in charge layer decreases. Compared to the thinner charge layer, the performance of APD varies significantly via several percent deviations of doping concentrations in the thicker charge layer. When designing APD structures, choosing a thin charge layer will give a high level of doping tolerance, as well as confer APD with good controllability. Finally, the G _btt of tunneling effect was calculated, and the influence of tunneling effect on the avalanche field was analyzed. We confirm that the avalanche field and multiplication factor (M _n ) in the multiplication will decrease by the tunneling effect.

Abreviações

2D:: Bidimensional
APD:: Avalanche photodiode
DCR:: Dark count rate
SACM APDs:: Separate absorption, charge, and multiplication avalanche photodiodes
SAGCMAPDs:: Separate absorption, grading, charge, and multiplication avalanche photodiodes
SPAD:: Single-photon avalanche photodiode
SPDE:: Single-photon detection efficiency
SRH:: Shockley–Read–Hall

Síntese Verde de Nanopartículas de Metal e Óxido de Metal e Seu Efeito na Alga Unicelular Chlamydomonas reinhardtii Sensor químico de etanol altamente sensível com base no novo α-Fe2O3 mesoporoso dopado com ag, preparado pelo processo Sol-Gel modificado

Nanomateriais

Materiais Poliméricos

biológico

Corante

Especiarias