Dois efeitos de transparência induzida por plasma selecionáveis em um sistema com ressonadores de grafeno distintos

Resumo

Os sistemas plasmônicos gerais para realizar o efeito de transparência induzida plasmonicamente (PIT) existem apenas um único PIT, principalmente porque eles permitem apenas uma única via de acoplamento. Neste estudo, propomos um sistema baseado em ressonador de grafeno distinto, que é composto de nanofitas de grafeno (GNRs) acopladas a ressonadores de camada de grafeno carregados com grade dielétrica, para atingir dois efeitos PIT comutáveis. Ao projetar direções cruzadas dos ressonadores, o sistema proposto existe dois diferentes efeitos PIT caracterizados por diferentes posições ressonantes e larguras de linha. Esses dois efeitos PIT resultam de duas vias de acoplamento separadas e seletivas de polarização, permitindo-nos mudar o PIT de um para o outro simplesmente mudando a direção da polarização. Estudos paramétricos são realizados para demonstrar os efeitos do acoplamento, enquanto o modelo de duas partículas é aplicado para explicar o mecanismo físico, encontrando excelentes concordâncias entre os resultados numéricos e teóricos. Nossa proposta pode ser usada para projetar dispositivos plasmônicos com base em PIT selecionáveis, como sensores sintonizáveis de banda dupla e absorvedores perfeitos.

Introdução

Plasmons de superfície são os modos de ressonância coletiva de elétrons livres que são gerados na interface entre os meios isolantes e condutores [1, 2]. Devido à sua capacidade de confinar um campo eletromagnético incidente ao tamanho limite final da escala de um átomo na faixa de comprimento de onda [3], os plasmons de superfície se tornaram um dos métodos mais fundamentais e importantes para alcançar fortes interações luz-matéria [4] . Este atraente fenômeno óptico foi encontrado em vários tipos de sistemas plasmônicos, o que facilita o desenvolvimento de uma variedade de aplicações de última geração, como biossensor [5], óptica não linear [6, 7], absorvedores [8,9] , 10,11], e outros moduladores plasmônicos [12,13,14,15]. As possibilidades de alcançar essas aplicações significativas são atribuídas a alguns fenômenos interessantes como a transparência induzida plasmonicamente (PIT). O processo conhecido como PIT é uma consequência da interferência Fano acoplada em campo próximo e é caracterizado pela geração de uma janela proeminente em um espectro óptico, pois elimina a absorção ressonante no sistema. Durante os últimos anos, essa interação plasmônica coerente tem sido usada para atingir uma variedade de aplicações, como comutação plasmônica [16], propagação lenta de luz [17] e detecção [18] e armazenamento óptico [19].

Embora estudos recentes tenham revelado que filmes de metal ultrafinos até a espessura atômica podem possuir sintonia elétrica dinâmica [20, 21], os plasmons suportados por esses novos metais ainda sofrem de perdas ôhmicas e radiativas relativamente grandes dos metais [22, 23]. Essa deficiência dos metais limita o desenvolvimento do PIT suportado por metal e é necessário encontrar novos materiais plasmônicos. Em contraste com os plasmons metálicos, os plasmons suportados por grafeno (uma única camada atômica de átomos de carbono fortemente estruturados formados em uma estrutura de favo de mel hexagonal simétrica) podem não apenas ser contínua e dinamicamente sintonizados através de polarização eletrostática [24, 25], mas também têm longa propagação comprimento, que permite uma nova geração de dispositivos plasmonic reestruturáveis e, portanto, fornece uma plataforma ideal para atingir PIT ativo [26, 27]. Embora vários materiais e projetos tenham sido usados para atingir PIT em metal puro [16, 28,29,30,31] e grafeno [32,33,34,35,36,37,38,39,40,41,42] , ou seus sistemas baseados em material híbrido [43,44,45], a maioria desses sistemas pode realizar apenas um único efeito PIT. Por exemplo, uma das maneiras comuns de obter PIT é projetar π metassuperfícies em forma de / semelhantes [16, 28, 30, 33, 37, 45]. Outra forma é construir sistemas acoplados a grades [32, 34]. No entanto, esses tipos de estruturas só podem realizar PIT de janela única dependente da polarização. Isso ocorre porque, devido à assimetria geométrica especial dessas estruturas, todos os ressonadores nanoestruturados são predefinidos para operar como modo brilhante (radiativo / superradiante) ou escuro (não radiativo / sub-radiante). Portanto, eles permitem apenas uma via de acoplamento claro a escuro em uma direção de polarização particular, resultando em apenas um efeito PIT dependente da polarização. Embora nossos estudos anteriores tenham demonstrado sistemas PIT com duas vias de acoplamento de modo claro-escuro em nanofitas de grafeno puro (GNRs) [35] ou estruturas acopladas em grade [38], o PIT de janela única insensível à polarização tally ou PIT de janela dupla dependente de polarização Os efeitos da janela PIT nestes sistemas dependem fortemente da escolha particular dos parâmetros geométricos (veja a parte de discussão).

Neste artigo, propomos o uso de dois ressonadores distintos, ou seja, GNRs acoplados a uma folha de grafeno carregada com grades dielétricas, para acoplar e realizar dois efeitos PIT separados. Vamos demonstrar que, definindo direções de ressonância perpendiculares, os plasmons de superfície que ressoam em ambos os ressonadores serão gerados sob diferentes direções de polarização da luz incidente, resultando em duas vias de acoplamento dependentes de polarização diferentes e, portanto, dois efeitos PIT separados. Além disso, estudos paramétricos serão utilizados para investigar em detalhes os mecanismos de acoplamento. E ambas as simulações avançadas e análises teóricas baseadas em modelos de duas partículas serão combinadas para demonstrar esses efeitos PIT selecionáveis. Por fim, serão discutidas as aplicações potenciais do sistema proposto, como sensores de índice de refração e absorvedores perfeitos, e as comparações com outros sistemas PIT.

Designs e materiais

Nesta parte, apresentamos o modelo numérico e os materiais relacionados usados neste estudo. Afirmamos que, em nosso modelo, consideramos apenas a eletrodinâmica clássica e negligenciamos quaisquer efeitos que possam surgir dos possíveis efeitos quânticos de tamanho finito de GNRs, efeitos não lineares de grafeno e efeitos de fônons de substrato [46]. O esquema do sistema proposto é mostrado na Fig. 1. Duas camadas de grafeno são colocadas no x o y plano e separados por um Si dopado ou SiO ₂ condutor com índice de refração n ₃ e espessura d . A primeira camada é formada por nanofitas de grafeno inferior (LGNRs) com um ponto no x direção. A segunda camada é uma folha de grafeno inteira, que é ainda coberta por grades dielétricas com um índice de refração n ₁ (rotulados como grades de grafeno superiores, UGGs) e um ponto final P _d no y direção. Os parâmetros geométricos são fixados como W _r = W _d =50 nm, p _r = p _d =100 nm, h =100 nm, e d =20 nm, conforme definido na Fig. 1. As constantes dielétricas dos outros materiais ao redor das camadas de grafeno são definidas como n ₀ e n ₂ , mostrado na Fig. 1. Para simplicidade e sem perda de generalidade, as constantes dielétricas são assumidas como n ₁ =2.0 e n ₀ = n ₂ = n ₃ =1,0. O desprezo da parte imaginária do índice de refração não mudaria as conclusões fundamentais deste estudo. Observe que os parâmetros acima permanecem os mesmos, a menos que seja especificado de outra forma. Tecnologicamente, a realização do sistema PIT baseado em grafeno de duas camadas projetado é experimentalmente viável usando as técnicas de padronização e grade bem desenvolvidas, que foram recentemente usadas para fabricar o sistema de grafeno em camadas [27, 47].

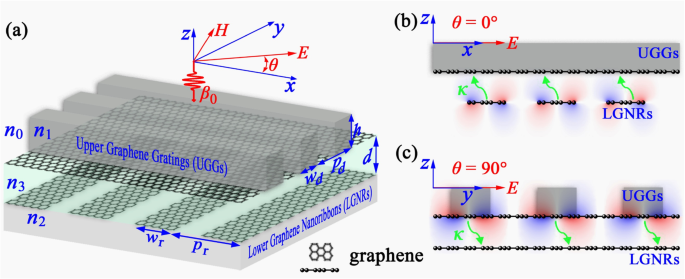
3D ( a ) e vistas laterais 2D ( b , c ) do sistema PIT proposto. Uma camada de grafeno carregada com grades dielétricas periódicas cobre acima de uma camada de GNRs periódicas com grades cruzadas e direções de fita. A camada superior da grade de grafeno é projetada com largura de grade W _d , altura h , e ponto transversal P _d , enquanto as nanofitas de grafeno inferiores têm largura de fita W _r e ponto final P _r . A distância entre as duas camadas de grafeno é d , que se presume ser preenchido por um Si condutivo ou SiO ₂ espaçador com índice de refração n ₃ . Os índices de refração de e sobre as grades dielétricas e abaixo dos GNRs são rotulados como n ₁ , n ₀ e n ₂ , respectivamente. Uma onda plana polarizada linearmente com número de onda β ₀ e ângulo de polarização θ em relação ao x - o eixo normalmente colide com a superfície do sistema de grafeno em camadas

Métodos

A estrutura proposta é simulada numericamente usando o método do domínio do tempo de diferenças finitas (FDTD) baseado em Soluções Numéricas de FDTD. Em nossas simulações, as condições de contorno periódicas são usadas nas direções x e y. Ondas planas de banda larga são incidentes na direção z, ao longo da qual camadas perfeitamente combinadas são aplicadas para absorver toda a luz que sai para os limites. A distribuição do campo elétrico é reunida por monitores de perfil de campo 2D no comprimento de onda ressonante com uma distância de 0,5 nm da superfície de grafeno entre as duas camadas. Além disso, o filme de grafeno é descrito dentro da aproximação de fase aleatória (RPA) [48, 49]. Dentro desta aproximação, a condutividade óptica no plano σ do grafeno é escrito como uma expressão semiclássica semelhante a Drude na faixa do infravermelho médio como σ ( ω ) = ie ² E _F / [ πћ ² ( ω + iτ ⁻¹ )] [24, 50]. Aqui, E _F = ћν _F ( n _g π ) ^1/2 é o nível de grafeno de Fermi, com n _g = ( μ / ћν _F ) ² / π sendo a concentração do portador (onde μ =15.000 cm ² / ( V × s ) é a mobilidade dc medida, ν _F =10 ⁶ m / s é a velocidade de Fermi, e ћ é a constante de Plank reduzida) e pode ser ajustada por portas elétricas [24, 25, 50], ω é a frequência angular, e τ =μE _F / ( ev _F ² ) é o tempo de relaxamento do portador. Neste artigo, E _F é fixado em 0,6 eV, a menos que especificado de outra forma. Em nossas simulações, a propriedade ótica do grafeno é descrita usando um tensor de permissividade relativa anisotrópica [35]. O z componente da permissividade do grafeno é definido como ε _zz =2,5 com base na constante dielétrica da grafite, enquanto os componentes no plano são ε _xx = ε _yy =2,5 + iσ ( ω ) / ( ε ₀ ωt ) [24, 51], com ε ₀ é a permissividade do vácuo e t =1 nm é a espessura do grafeno [35].

Aplicando o modelo de duas partículas em ambos os x e y eixos, podemos teoricamente analisar as ressonâncias plasmônicas efetivas e os acoplamentos mostrados na Fig. 1 pelo seguinte conjunto de equações [8, 52, 53]:
$$ {a} _ {1i} ^ {{\ prime \ prime}} (t) + {\ gamma} _ {1i} {a} _ {1i} ^ {\ prime} (t) + {\ omega} _ {1i} ^ 2 {a} _ {1i} (t) + {\ kappa} _ {12i} ^ 2 {a} _ {2i} (t) ={Q} _ {1i} E \ sin \ theta / {m} _ {1i} $$ (1) $$ {a} _ {2i} ^ {{\ prime \ prime}} (t) + {\ gamma} _ {2i} {a} _ {2i} ^ {\ prime} (t) + {\ omega} _ {2i} ^ 2 {a} _ {2i} (t) + {\ kappa} _ {21i} ^ 2 {a} _ {1i} (t) ={Q} _ {2i} E \ cos \ theta / {m} _ {2i} $$ (2)
onde eu = x ou y ; γ _i é o fator de perda, que se relaciona com a largura de linha do espectro; ω _i é a frequência de ressonância do ressonador; Q _i são as cargas efetivas dos modos, que mostram a força do modo ressonante; e m _i é a massa efetiva das partículas na orientação ressonante correspondente. κ _i é a força de acoplamento entre as duas camadas no i direção, que corresponde às interações elétron-elétron dos dois modos acoplados e, portanto, é determinada pela distribuição de campo especial dos plasmons e a distância de acoplamento entre os ressonadores. Considerando que os acoplamentos plasmônicos estão apenas ao longo dos dois eixos coordenados com força de acoplamento κ _{12 i} = κ _{21 i} = κ _i , podemos tratar o sistema como dois grupos separados de ressonadores ressoando independentemente em direções diferentes. Assumimos que todas as partículas se acoplam ao campo elétrico incidente E = E ₀ e ^iωt , gerando os vetores de deslocamento a _i = c _i e ^iωt . Depois de realizar alguns cálculos algébricos nas Eqs. (1) e (2), as amplitudes de modo dos plasmons podem ser expressas como:
$$ {a} _ {1i} (t) =\ frac {\ kappa_i ^ 2 {Q} _ {2i} E \ cos \ theta / {m} _ {2i} + \ left ({\ omega} ^ 2 -i {\ omega \ gamma} _ {2i} - {\ omega} _ {2i} ^ 2 \ right) {Q} _ {1i} E \ sin \ theta / {m} _ {1i}} {\ kappa_i ^ 4- \ left ({\ omega} ^ 2-i {\ omega \ gamma} _ {1i} - {\ omega} _ {1i} ^ 2 \ right) \ left ({\ omega} ^ 2-i { \ omega \ gamma} _ {2i} - {\ omega} _ {2i} ^ 2 \ right)} $$ (3) $$ {a} _ {2i} (t) =\ frac {\ kappa_i ^ 2 { Q} _ {1i} E \ sin \ theta / {m} _ {1i} + \ left ({\ omega} ^ 2-i {\ omega \ gamma} _ {1i} - {\ omega} _ {1i} ^ 2 \ direita) {Q} _ {2i} E \ cos \ theta / {m} _ {2i}} {\ kappa_i ^ 4- \ left ({\ omega} ^ 2-i {\ omega \ gamma} _ {1i} - {\ omega} _ {1i} ^ 2 \ right) \ left ({\ omega} ^ 2-i {\ omega \ gamma} _ {2i} - {\ omega} _ {2i} ^ 2 \ direita)} $$ (4)
A suscetibilidade elétrica efetiva ( χ _eff ), que mostra a razão entre a polarizabilidade total ( P ) dos ressonadores plasmônicos e a força do campo elétrico incidente, então podem ser expressos nas formas dos vetores de deslocamento como:
$$ {\ displaystyle \ begin {array} {c} {\ chi} _ {e \ mathrm {ff}, i} =\ frac {P_i ^ 2} {\ varepsilon_0E} =\ frac {Q_ {1i} {a } _ {1i} + {Q} _ {2i} {a} _ {2i}} {\ varepsilon_0E} \\ {} =\ frac {\ left [{\ kappa} _i ^ 2 {Q} _ {1i} {Q} _ {2i} + \ left ({\ omega} ^ 2-i {\ omega \ gamma} _ {2i} - {\ omega} _ {2i} ^ 2 \ right) {Q} _ {1i} ^ 2 \ direita] \ sin \ theta / {m} _ {1i} + \ esquerda [{\ kappa} _i ^ 2 {Q} _ {1i} {Q} _ {2i} + \ esquerda ({\ omega} ^ 2-i {\ omega \ gamma} _ {1i} - {\ omega} _ {1i} ^ 2 \ direita) {Q} _ {2i} ^ 2 \ direita] \ cos \ theta / {m} _ { 2i}} {\ varepsilon_0 \ left [{\ kappa} _i ^ 4- \ left ({\ omega} ^ 2-i {\ omega \ gamma} _ {1i} - {\ omega} _ {1i} ^ 2 \ direita) \ left ({\ omega} ^ 2-i {\ omega \ gamma} _ {2i} - {\ omega} _ {2i} ^ 2 \ right) \ right]} \ end {array}} $$ ( 5)
Então, os espectros de transmissão e absorção simulados podem ser ajustados pela parte imaginária da susceptibilidade. Neste artigo, a absorção é definida como A =Im [ χ _{eff, i} ] Este coeficiente é derivado da conservação da relação de energia T + A =1; portanto, temos a expressão da transmissão T =1 - Im [ χ _{eff, i} ]

Resultados

Excitação dos efeitos PIT

Para estimular os efeitos do PIT, um problema que precisa ser resolvido é como projetar um ressonador de modo brilhante. Por causa da grande incompatibilidade de momento entre as ondas de espaço livre de entrada e as ondas de plasmon, a excitação de plasmons é um dos principais desafios para o uso de plasmons de grafeno. Para terminar, várias abordagens que permitem a excitação de plasmons de grafeno foram propostas e demonstradas teórica e experimentalmente. O primeiro método comumente usado é padronizar a monocamada de grafeno para nanoestruturas coplanares, como nanofitas [25, 54], nanodiscos [55, 56] e círculos [24]. Outro método é construir configurações de grade em uma folha de grafeno contínua, o que é conseguido usando as grades dielétricas difrativas [51, 57] e as portas de campo elétrico [58] para construir grades de condutividade local periódicas dependentes da posição ou usando difrativas periódicas grades onduladas formadas pela própria folha de grafeno [57, 59]. A razão pela qual os plasmons de superfície podem ser excitados nessas estruturas de grafeno é que as nanoestruturas ou grades podem fornecer às ondas de plasmon um vetor de ondas recíproco adicional que é necessário para a compensação da incompatibilidade do vetor de ondas quando a direção de polarização está ao longo da direção periódica [51 , 54, 59]. Nesta condição, o ressonador de grafeno pode operar como um modo claro ou pode funcionar como um modo escuro. Aqui, propomos o uso de GNRs e a folha de grafeno carregada com grades dielétricas de forma retangular para trabalhar respectivamente como modos claro e escuro para construir um sistema PIT, como mostrado na Fig. 1.

Para explorar o mecanismo do sistema PIT proposto, simulações numéricas da configuração mostrada na Fig. 1 são calculadas e os resultados correspondentes para dois ângulos de polarização diferentes são mostrados na Fig. 2. Para o caso com θ =0 °, primeiro calculamos os resultados para a situação em que as nanofitas de grafeno inferiores (LGNRs) e o grafeno carregado com grade dielétrica superior existem sozinhos. Como a direção de polarização é perpendicular aos LGNRs, os SPs podem ser excitados neles, resultando em um pico de absorção principal em 5,327 μm, como a linha azul mostrada na Fig. 2a. Em contraste, os SPs na folha de grafeno superior não podem ser excitados nesta condição de polarização porque a luz incidente é polarizada paralelamente às grades dielétricas, resultando em uma incompatibilidade de momento forte, como é demonstrado pelas linhas verdes planas na Fig. 2a. Nessas situações, nos referimos ao modo diretamente excitado nos LGNRs e ao modo escuro nos UGGs como LGNRs-0 e UGGs-0, respectivamente, conforme mostrado nas Fig. 2g e f. No entanto, o que é interessante aqui é que quando essas duas camadas de grafeno são colocadas juntas e próximas o suficiente, dois picos de absorção (quedas de transmissão) aparecem em 5,747 μm e 4,917 μm. Aquele com comprimento de onda ressonante mais longo é dominante por absorção atingindo 47,16%, enquanto o outro com comprimento de onda ressonante mais curto é caracterizado por um pico de absorção de 35,88%, indicando que esses dois modos interagem fortemente com a luz incidente externa, como mostrado na Fig. .2a e concluído na Tabela 1. Esses dois modos se originam dos acoplamentos plasmônicos em fase e fora de fase entre os dois ressonadores. Especificamente, o modo de ressonância brilhante nos LGNRs deve ser considerado um modo fixo porque é diretamente excitado pela luz incidente. No entanto, a ressonância de plasmon na camada superior de grafeno não pode ser diretamente excitada, mas pode se acoplar àquelas excitadas nos LGNRs por meio de interações em fase e fora de fase. É a coexistência dos dois ressonadores e seus acoplamentos plasmônicos que resultam diretamente neste efeito PIT. Para revelar os mecanismos físicos por trás da origem dos dois modos claramente, exibimos as distribuições do campo elétrico nesses dois modos na Fig. 2h e i. De acordo com o E _z distribuições de campo de componentes, o modo em 5,747 μm mostra uma natureza de ressonância em fase da estrutura em camadas e, portanto, é chamado de modo simétrico. O modo em 4,917 μm mostra a ressonância antifásica e é chamado de modo antissimétrico. Além disso, as Fig. 2h e eu revelam claramente a estrutura desses modos:Todos os E _z componentes mostram uma ressonância de modo dipolo caracterizado por 2 π mudança de fase ao longo da direção de polarização ( x eixo) em cada camada de grafeno. Esses dois modos fundamentais eliminam a absorção ressonante dos LGNRs enquanto dão origem a uma janela de transmissão proeminente e dois picos de absorção no espectro óptico, causando o efeito óptico chamado PIT (para a conveniência da discussão, chamamos isso de LGNRs-PIT). Na Fig. 2c, também representamos graficamente a fase de transmissão e o tempo de atraso nos dois picos de absorção, os últimos atingindo 0,34 ps e 0,36 ps, respectivamente, indicando o efeito de desaceleração da luz no sistema.

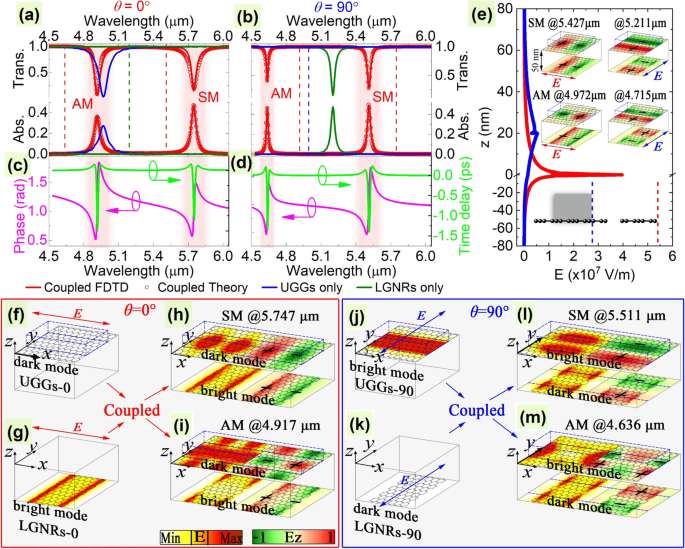
Linhas de transmissão e absorção ( a , b ) e sua fase de transmissão (esquerda y eixo) e tempo de atraso (direita y eixo) ( c , d ) do sistema com ângulo de polarização θ =0 ° ( a , c ) e 90 ° ( b , d ), respectivamente. Em ( a ) e ( b ), as linhas tracejadas mostram a posição ressonante na outra polarização. Os parâmetros de ajuste das linhas teoricamente analisadas em ( a ) e ( b ) são (em THz) 6,71, 110,07, 2,25, 0,46 e 0,74 e 5,73, 4,13, 72,83, 0,33 e 0,27 para κ _i , Q _1i / sqrt ( ε ₀ m _1i ), Q _2i / sqrt ( ε ₀ m _2i ), γ _1i , e γ _2i , respectivamente. Distribuições espaciais do campo elétrico para os casos com UGGs ( e (linha azul), f , j ) e LGNRs ( e (linha vermelha), g , k) apenas ao longo do z eixo ( e ) e nos planos de grafeno correspondentes ( f , g , j , k ) Distribuições espaciais do campo elétrico (painéis à esquerda) e o correspondente z componente (painéis direitos) do modo simétrico (SM) ( h , @ 5,747 μm; l , @ 5.511 μm) e modo anti-simétrico (AM) ( i , @ 4,917 μm; m , @ 4,636 μm) em ângulos de polarização θ =0 ° ( h , i ) e 90 ° ( l , m ), respectivamente. As inserções superiores em e mostrar z componente do campo elétrico para o caso com d =50 nm, enquanto a inserção inferior representa a posição do campo no gráfico principal. Os sinais “+” e “-” doam as cargas de superfície ressonantes; a cor mais escura se refere a uma densidade de carga maior

Enquanto para o caso com θ =90 °, os SPs podem ser excitados em UGGs com um pico de absorção principal em 5,202 μm, mas não nos LGNRs quando existem sozinhos, como as linhas verde e azul mostradas na Fig. 2b, respectivamente. Nessas situações, nos referimos ao modo diretamente excitado nos UGGs e ao modo escuro nos LGNRs como LGNRs-90 e UGGs-90, respectivamente, conforme mostrado nas Fig. 2j e k. No entanto, quando esses dois modos estão próximos o suficiente para se acoplarem, duas quedas de transmissão (picos de absorção) aparecem claramente em 5,511 μm e 4,636 μm com absorção atingindo 49,07% e 46,46%, respectivamente, o que significa que as interações com as ondas incidentes externas são muito fortes, como mostrado na Fig. 2b e concluído na Tabela 1. Semelhante ao caso com θ =0 °, o mecanismo físico também pode ser compreendido considerando os acoplamentos de plasmon em fase e fora de fase entre as duas camadas de grafeno. Como é claramente ilustrado pela Fig. 2l e m, o E _z distribuições de campo de componente mostram uma ressonância de modo dipolo caracterizado por 2 π mudança de fase ao longo do y eixo em cada camada de grafeno e revelar ressonâncias em fase (modo simétrico) e fora de fase (modo antissimétrico) nos picos de absorção correspondentes. São esses dois modos fundamentais que eliminam a absorção ressonante do caso apenas com os UGGs, enquanto geram uma janela de transmissão proeminente e dois picos de absorção no espectro óptico, resultando em outro PIT (para a conveniência da discussão, chamamos isso de UGGs-PIT ) Na Fig. 2d, a fase de transmissão e o tempo de atraso nos dois picos de absorção também são representados, mostrando o efeito de propagação da luz em desaceleração com valores de pico de 0,23 ps e 0,21 ps no modo simétrico e no modo anti-simétrico, respectivamente.

No entanto, é importante notar que embora as distribuições de campo na folha de grafeno superior do modo antissimétrico na Fig. 2i e m mostrem uma aparência ressonante "multipolo", elas ainda são um modo dipolo, pois as oscilações de carga também mantêm a natureza de uma ressonância de modo dipolo ao longo da direção de polarização. A razão para a aparência ressonante “multipolar” é devido à forte interferência de campo dos LGNRs. Isso pode ser entendido considerando o fato de que o campo de plasmon localizado mais forte nas GNRs padronizadas é mais pronunciado do que na folha de grafeno contínua [60], como mostrado na Fig. 2e. Estas aparências de modo "multipolo" desaparecerão, definindo o monitor de campo fora das duas camadas de grafeno ou usando uma grande distância de acoplamento, por exemplo, quando d =50 nm, as aparências do modo “multipolo” mudarão para a ressonância do modo dipolo puro, conforme mostrado nas inserções da Fig. 2e. Além disso, também notamos que os acoplamentos de modo entre as duas camadas de grafeno são diferentes. Especificamente, para o caso com θ =0 °, o LGNRs-PIT é o resultado do forte acoplamento entre LGNRs-0 e UGGs-0, que são ressonantes ao longo do x direção. Enquanto para o caso com θ =90 °, o UGGs-PIT é o resultado do forte acoplamento entre UGGs-90 e LGNRs-90, que são ressonantes ao longo do y direção, como mostrado claramente na Fig. 2. Assim, o LGNRs-PIT e UGGs-PIT são os efeitos de acoplamentos plasmônicos entre diferentes modos de ressonância em polarizações diferentes, resultando em dois efeitos PIT diferentes.

Portanto, podemos concluir da Fig. 2 que o LGNRs-PIT (com θ =0 °) e UGGs-PIT (com θ =90 °) são dois efeitos PIT diferentes resultantes de duas vias separadas de acoplamento de modo claro para escuro do sistema de grafeno em camadas e fretado pela resposta espectral diferente. Isso significa que podemos mudar esses dois efeitos PIT de um para o outro apenas mudando a direção de polarização da luz incidente, que é muito diferente do efeito PIT insensível à polarização (consulte a parte de discussão). Além disso, esse efeito PIT comutável pode ser explicado pelo modelo de duas partículas mostrado nas Eqs. (1) e (2). Para o caso com θ =0 °, a eficiência de acoplamento direto de UGGs ao campo incidente é zero (escuro) enquanto que a dos LGNRs é a mais alta (claro), conforme demonstrado pelo lado direito das equações. Enquanto para o caso com θ =90 °, vice-versa, os UGGs ficam claros enquanto os LGNRs ficam escuros. Observe que em ambos os casos, a concordância entre os resultados analíticos obtidos com a Eq. (5) (representado por círculos vermelhos na Fig. 2a, b) e os resultados numéricos (plotados com linhas vermelhas na Fig. 2a, b) são quase perfeitos. Nosso modelo analítico prevê com muita precisão não apenas as posições, mas também os valores de pico das ressonâncias, como está claro na Fig. 2. Finalmente, notamos aqui que os resultados apresentados aqui são muito diferentes de outros sistemas PIT que são construídos com o mesmos ressonadores [35, 38]; isso ocorre porque eles não podem obter os resultados mostrados na Fig. 2 sob polarizações diferentes. Discutiremos as diferenças mais adiante na parte de discussão.

Ajustabilidade geométrica do PIT

Demonstramos que os acoplamentos de campo próximo entre os modos claro e escuro resultam em dois efeitos PIT dependentes da polarização; portanto, os parâmetros que afetam muito as ressonâncias de modo claro e escuro, bem como a força de acoplamento entre eles, podem ser tratados como um parâmetro ajustável para os efeitos PIT. Primeiramente, realizamos estudos paramétricos para o caso com θ =0 ° mudando a largura ( W _r ) dos LGNRs e as larguras ( W _d ) dos UGGs de 20 a 100 nm, e mostram os resultados nas Fig. 3a e c, respectivamente. Como os LGNRs se acoplam diretamente à luz incidente e funcionam como o modo brilhante nessas condições, qualquer mudança em suas dimensões afeta diretamente toda a resposta plasmônica do sistema. Por exemplo, quando W _r é muito pequeno, por exemplo, 20 nm, a eficiência de acoplamento com a luz incidente é muito fraca devido à baixa taxa de ocupação dos GNRs [14, 51], resultando em baixa absorção do modo anti-simétrico e principalmente do modo simétrico do sistema PIT, como pode ser visto na linha de absorção de W _r =20 nm na Fig. 3a. Como outro exemplo, quando W _r é grande o suficiente, e especialmente quando atinge seu máximo de 100 nm (isto é, quando os LGNRs são uma camada inteira de grafeno), nenhum dos dois ressonadores pode acoplar com o campo externo e, assim, o LNGRs-PIT desaparece. Notavelmente, as absorções dos dois modos mostram os valores mais altos simultaneamente quando W _r é cerca de 50 nm. Diferente do modo brilhante, as variações da largura DG ( W _d ) na camada superior de grafeno para o modo escuro pode apenas sintonizar as posições ressonantes e as absorções do modo simétrico e do modo antissimétrico dentro dos limites, enquanto não pode eliminar ou mesmo afetar significativamente a alta eficiência de acoplamento com as ondas externas, como mostrado na Fig. 3c. Na verdade, mesmo quando as grades dielétricas são removidas ou se tornam uma camada dielétrica inteira ( W _d =100 nm), os LGNRs ainda podem acoplar com a folha de grafeno superior, como foi demonstrado por um caso bidimensional descrito em um trabalho anterior [36], onde apenas um efeito PIT é permitido existir.

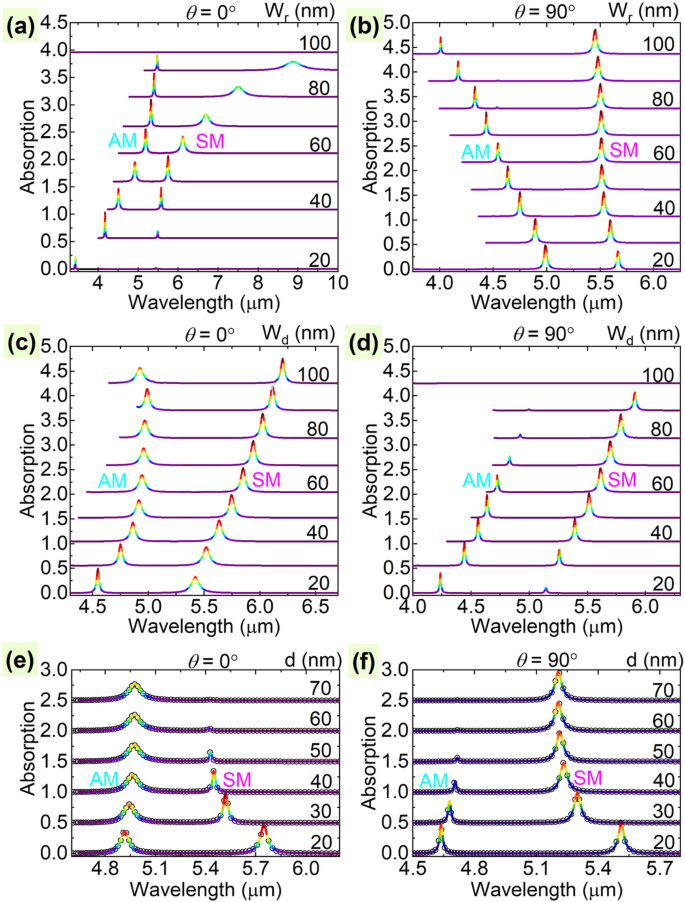
Os espectros de absorção do sistema PIT na escala de comprimento de onda como funções de ( a ), ( b ) a largura da fita W _r de LGNRs; ( c , d ) a largura do DG W _d de UGGs; e ( e , f ) a distância de separação d entre as duas camadas de grafeno com um passo de 10/20 nm em ângulos de polarização de θ =0 ° ( a , c , e ) e 90 ° ( b , d , f ), respectivamente. Em ( a - f ), a cor vermelha mais profunda nas linhas sólidas denota uma absorção mais forte. Observe que algumas das linhas são cortadas para evitar distrações de outros picos de absorção de ordem superior. Em ( e ) e ( f ), curvas sólidas e olheiras apresentam os resultados numéricos e teóricos, respectivamente. SM e AM referem-se ao modo simétrico e modo anti-simétrico, respectivamente

No entanto, para o caso com θ =90 °, os resultados estão em contraste com o caso com θ =0 ° porque os LGNRs funcionam como um modo escuro enquanto os UGGs funcionam como um modo claro. Em detalhe, a mudança da largura LGNR W _r modula apenas as posições ressonantes e as absorções máximas do modo simétrico e do modo antissimétrico, não podendo extinguir a existência dos dois modos, como mostra a Fig. 3b. Isso ocorre porque os LGNRs operam como um modo escuro nesta condição de polarização. Na condição com W _r =100 nm, o sistema se torna uma folha de grafeno carregada com DG acopla-se a outra folha de grafeno, que é semelhante a um sistema PIT único bidimensional relatado anteriormente em outro estudo [34]. No entanto, a mudança das grades dielétricas superiores terá um grande impacto na resposta óptica do sistema PIT, já que a folha de grafeno superior funciona como um modo brilhante nesta condição, que é muito semelhante ao caso ao mudar W _r com θ =0 °, conforme mostrado na Fig. 3d. Em geral, podemos concluir da Fig. 3a – d que o ajuste do modo brilhante afetará muito a aparência e até mesmo a existência dos UGGs-PIT, como são demonstrados nas Fig. 3a e d, enquanto a mudança do o modo escuro só pode alterar as posições ressonantes e as intensidades relativas do modo simétrico e do modo anti-simétrico no UGGs-PIT, conforme mostrado nas Fig. 3b e c.

Outro parâmetro que afeta muito os efeitos do PIT é o espaço d entre os dois ressonadores de grafeno. Conforme corrigimos as larguras dos GNRs e grades dielétricas e, em seguida, aumentamos d , the interaction strength between the two graphene resonators decreases monotonically for both polarization angles due to the fast decreasing plasmonic field in the normal direction of the graphene surface [35, 61]. As a result, the symmetric mode and the antisymmetric mode are respectively extinguished for the case with θ =0° and θ =90° at large coupling distance, e.g., d> 70 nm, as shown in Fig. 3e and f. As it is known that when the bright and dark modes are far beyond the decay length of the evanescent field of each other, these two modes are uncoupled, and therefore, only the bright mode exists. At that point, we can conclude from Fig. 3e and f that the symmetric mode and antisymmetric mode of the PIT respectively originate from the UGGs and LGNRs, as they remain at large layer distance. Note that the PIT effects at different coupling strengths match well with the two-particle model, as the simulated and analytically predicted results are in excellent agreement, as can be seen in Fig. 3a and b, where the solid curves are gotten from FDTD, and the dark circles are from the two-particle model.

Electrical Tunability of PIT

One of the major advantages of graphene-based plasmonic devices is their dynamic and broadband tunability, which can be realized by electrostatic gating techniques [61, 62]. This intriguing property allows us to electrically change the Fermi energy of graphene and, thus, to actively modulate the transmission window of the proposed PIT systems to work at different wavelengths without reconstructing the geometrical structure [24, 25]. By applying different bias voltages with a field-effect transistor structure, researchers have experimentally achieved the dynamical tune of the Fermi energy level from 0.2 to 1.2 eV [63]. The simulated absorption spectra shown in Fig. 4 confirms the broadband and dynamic tunability of the proposed PIT device. For the given geometrical parameters, the plasmon wavelengths of the symmetric mode and antisymmetric mode of the LGNRs-PIT (UGGs-PIT) can be tuned from 4.977 to 9.953 μm and 4.259 to 8.520 μm (from 4.775 to 9.551 μm and 4.015 to 8.033 μm) when the Fermi level is modulated from 0.8 to 0.2 eV, respectively, as the solid and dash-dotted lines shown in Fig. 4a and b. This dynamic tunability will greatly facilitate the design and practical application of the proposed PIT device.

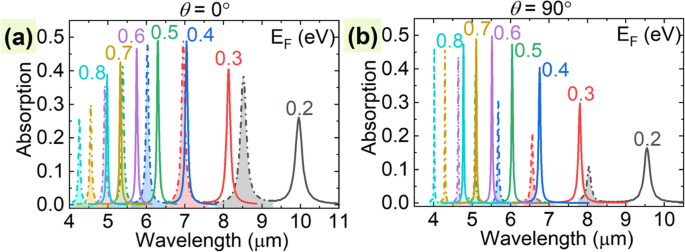
Absorption spectra of the symmetric mode (solid lines) and antisymmetric mode (dash-dotted lines) of the proposed PIT system with different Fermi energy levels of graphene at polarization angles of θ =0° (a ) and 90° (b ), respectivamente

Applications

In the previous parts, we have made clear how the LGNRs couple with the UGGs and further result in the polarization-dependent PIT effects, and demonstrated how the geometrical and electrical parameters affect the couplings. In this part, we will demonstrate our proposal can be used as selective refractive index sensors and dual-band perfect absorbers.

Considering that the PIT effect is determined by both the bright and dark mode resonances, what brings the change to these two modes will directly alter the symmetric mode and antisymmetric mode in the PIT window. Therefore, the induced symmetric mode and antisymmetric mode are highly sensitive to the local dielectric environment, which can be applied to design refractive index sensors [64]. In our design, both the regions above the UGGs (with refractive index n ₀ ) and below the LGNRs (with refractive index n ₂ ) can be thought of as the sensing regions. To calculate the sensitivities, we define S =Δλ/ Δn , which specifies the plasmon wavelength (λ ) shift per refractive index unit (RIU). We assume the refractive indexes of the materials as n ₁ =2.0 and n ₀ =n ₂ =n ₃ =1.3 (except the cases when n ₀ or n ₂ is working as the sensing regions with the range changing from 1.0 to 1.1).

Firstly, when tuning the width of the GNRs (W _r ), we find that when the sensing region is alongside the bright mode (that are sensing region n ₀ with θ =90° and sensing region n ₂ with θ =0°), the sensitivity of the symmetric mode S _SM gets bigger at wider ribbon width (see the solid blue lines in Fig. 5b, c). Especially, S _SM can reach 4 μm/RIU for the case with θ =0° in sensing region n ₂ . Secondly, for the case with increasing DG width (W _d ), both the sensitivity of the symmetric mode S _SM and antisymmetric mode S _AM decrease in most cases. Finally, as for the coupling distance d between the two layers, it is found that S _SM decreases while that of the antisymmetric mode increases for both of the polarization angles (see the solid and dash-dotted dark lines in Fig. 5). Considering that the antisymmetric mode will disappear under large coupling distance at the polarization angle of θ =90° (see Fig. 3f), the antisymmetric mode for the situation with θ =0° is more suitable to work as a sensor at a larger distance. Generally, the sensitivities of the symmetric mode and antisymmetric mode of the LGNRs-PIT and UGGs-PIT are respectively comparable to each other, as can be concluded by comparing Fig. 5a with 5b, and Fig. 5c with 5d, respectively. Besides, it is also found that the sensitivities for the cases with sensing regions alongside the bright and dark modes do not show a big difference, as can be seen by comparing Fig. 5a with 5d (alongside the dark mode), and Fig. 5b with 5c (alongside the bright mode). However, the sensitivities of the case with the sensing region under the LGNRs are obviously higher than that of the case with the sensing region above the UGGs, as they are shown by comparing Fig. 5a and b with Fig. 5c and d. This is because the sensitivity is directly related to the localized plasmonic field [64], and the local plasmonic field in the cutting-edge nanoribbons is generally stronger than the continuous edge-free graphene dielectric gratings [60].

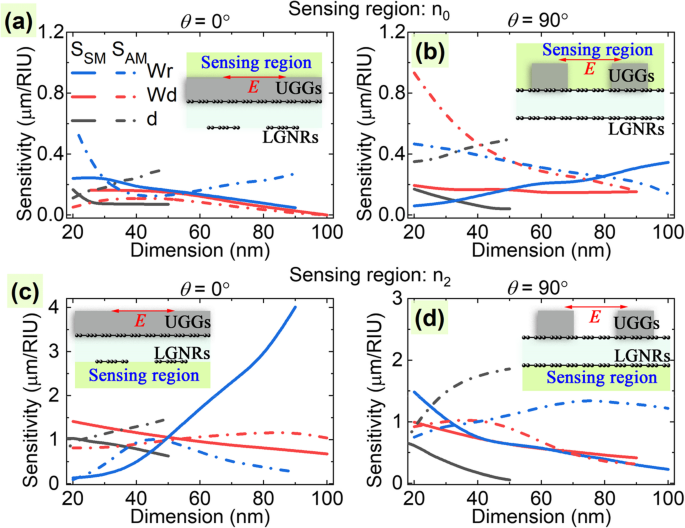
Refractive index sensitivities of the symmetric mode (S_SM , solid lines) and antisymmetric mode (S_AM , dash-dotted lines) in the sensing regions of n ₀ ( a , b ) and n ₂ ( c , d ) as functions of the ribbon width W _r of LGNRs, the DG width W _d of UGGs, and the separation distance d between the two graphene layers at polarization angles of θ =0° (a , c ) and 90° (b , d ), respectivamente. The inserts show the location of the sensing region

Besides working as a refractive index sensor, the proposed system can also be further designed as a perfect absorber. To achieve this, we can add a metallic substrate below the LGNRs and assume the refractive indexes of the materials as n ₁ =2.0 and n ₀ =n ₂ =n ₃ =1.3. With the existence of the metallic substrate, the dielectric layer between the LGNRs and metallic mirror forms a Fabry-Perot cavity, which can increase the interaction of incidence with graphene layers and further increase the absorptivity of the two modes. For the LGNRs-PIT case with θ =0°, we find that perfect absorptions with absorptivity> 96% of the symmetric mode and antisymmetric mode can be achieved simultaneously when the metallic substrate is with a 3.0-μm distance below the LGNRs, as shown in Fig. 6a and c. We also find that our proposal has good robustness to the doping level of graphene, as shown in Fig. 6a. The absorptivity of the two modes is> 90% when the Fermi energy level of graphene ranges from 0.58 to 0.66 eV. Besides the doping level of graphene, the perfect absorptions also show good tolerance to the polarization angle:The absorptivity of the two modes can keep at a high level (>90%) even the polarization angle ranges from − 17 to 17°. The robustness to the parameters is good for the practical design of the absorber.

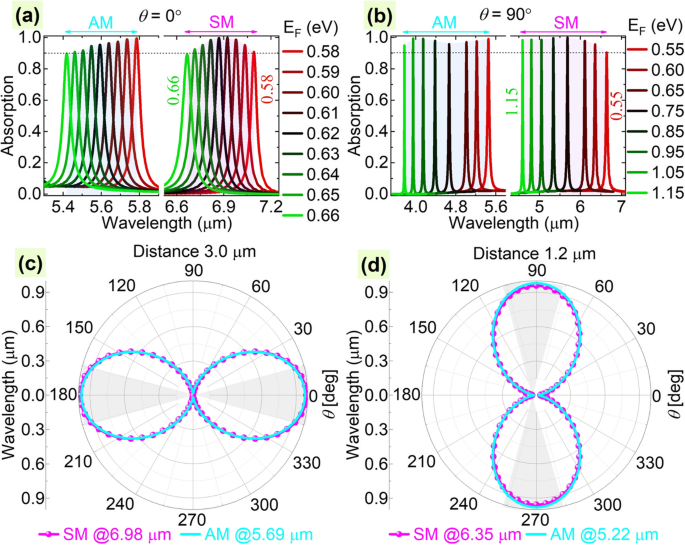
Absorption spectra with different Fermi energy levels of graphene at polarization angles of θ =0° (a ) and 90° (b ) for the cases with a metal substrate below the LGNRs with a distance of 3.0 μm (a , c ) and 1.2 μm (b , d ), respectivamente. ( c , d ) Absorption maxima as functions of θ . SM and AM refer to the symmetric mode and antisymmetric mode, respectively

To achieve the perfect absorption for the UGGs-PIT case with θ =90°, we need to set the metallic substrate with a 1.2-μm distance below the LGNRs. It is found that perfect absorptions with absorptivity> 95% of the symmetric mode and antisymmetric mode can be achieved simultaneously, as shown in Fig. 6b and d. Similar to the LGNRs-PIT case, it also found that the perfect absorptions show good tolerance to the polarization angle ranging from − 15 to 15° with absorptivity of the two modes> 90% (see Fig. 6d). More notably, the proposed absorber for the UGGs-PIT case shows much bigger robustness to the doping level of graphene, as plotted in Fig. 6b. It is found that the absorptivity of the two modes is> 90% even the Fermi energy level of graphene ranges from 0.55 to 1.15 eV. Considering that the Fermi level of graphene can be dynamically tuned by an external gate voltage, the designed structure can be thought of as active dual-band perfect absorber with a working wavelength of the symmetric mode (antisymmetric mode) ranging from 4.59 to 6.64 μm (3.77 to 5.45 μm).

Discussions

In this part, we discuss the advantages and differences of the proposed structure with other similar structures. To this end, we first calculated the plasmon resonant wavelengths for the cases with only the GNRs and only the dielectric grating-loaded graphene, as shown in Fig. 7a. It shows that the plasmon wavelengths have different dependencies on the width of the resonator. Besides, the inserts show the resonant property of the modes:For GNRs, the plasmonic fields are mainly localized on the edge of the GNR, while for the case with graphene sheet attached with dielectric gratings, the plasmonic fields are mainly concentrated on the grating area. Previous studies have shown that the field distributions and the distance between the resonators will greatly affect the plasmonic couplings [35, 65] and, therefore, the spectral response of the coupled system. That is to say, in our cases, the couplings from the LGNRs to the upper dielectric gratings are different from the other way coupled from the upper dielectric gratings to the LGNRs. Therefore, we obtain the results shown in Fig. 7b that even when the plasmon wavelengths of the two resonators are the same when they exist alone, they will also lead to two distinct PIT effects no matter what they work as bright or dark modes. To show more clearly the advantage of our design, we plot the resonant mode positions of the PIT effects for different geometrical parameters in Fig. 7c and d. They clearly demonstrate that there are always two distinguishable PIT effects for the two polarization directions, even when the geometrical parameters are the same.

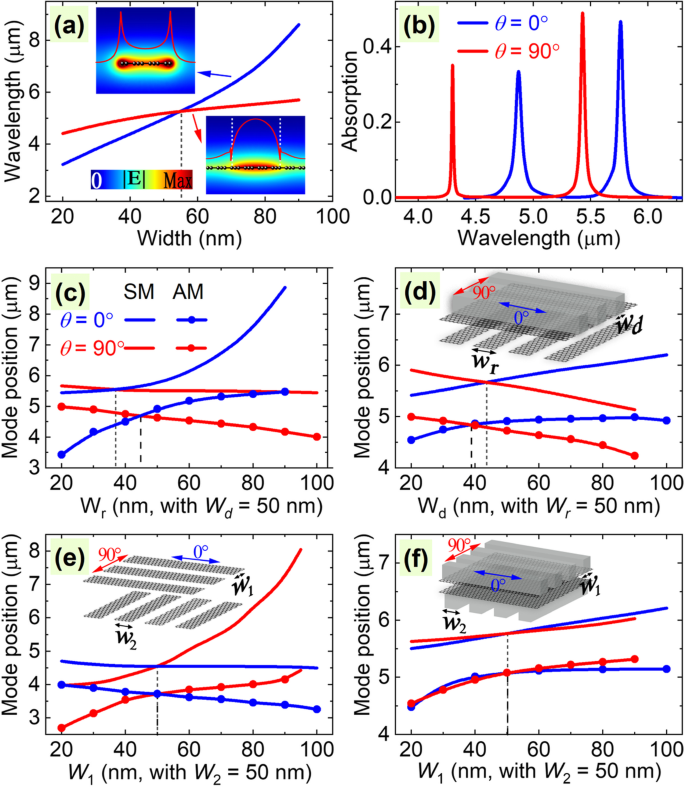
( a ) Plasmon wavelengths of the cases with only the GNRs and only dielectric grating-loaded graphene sheet for different ribbon and grating width. The inserts show the field distribution of the modes. ( b ) Absorption spectra for different polarization angles of GNR and dielectric grating-loaded graphene-coupled system with their width of 54 nm. ( c - f ) Resonant positions of the two PIT peaks at different polarization angles for different systems. The inserts show the corresponding structures

However, one may want to know why the proposed structure is not designed with the same resonators, such as perpendicular GNRs and dielectric grating-loaded graphene, as it has been reported in the previous studies [35, 38]. To explain this, we have plotted the resonant positions of the two modes in the PIT effects for the structures with pure GNRs and dielectric grating-loaded graphene resonators in Fig. 7e and f, respectively. It is found that when the two layers of resonators are designed with the same geometrical parameters, there is only one PIT effect for all the polarization directions, which means the PIT effect becomes indistinguishable from the absorption spectrum. This is because the couplings between the two layers of resonators are equivalent due to the same field distribution of the plasmon modes. That is to say, the polarization-independent PIT effects of the structures shown in the insert of Fig. 7e and f depend on the particular choice of the geometrical parameters. Whereas, on the contrary, the design in this paper to achieve two switchable PIT effects is not dependent on the particular choice of the geometrical parameters, which can guarantee the existence of the two switchable PIT effects.

Conclusão

In this paper, both advanced simulations and theoretical analyses are combined to investigate switchable PIT effects in two graphene layers formed by GNRs coupled with a dielectric grating-loaded graphene layer. Thanks to the crossed nanoribbon and grating directions, both the GNRs and the dielectric gratings can operate as either the bright or the dark mode depending on the polarization direction. The incident light under these two polarization directions introduces two different bright to dark mode coupling pathways within the two resonators, resulting in two switchable PIT effects. Geometrical parameters, such as graphene nanoribbon width, dielectric grating width, layer distance, and graphene Fermi level, are used to study the physical mechanism and the performance of the proposed PIT effect. Additionally, the proposed concepts are examined by applying a two-particle model, showing outstanding agreement with the numerical results. The proposed methods provide a general approach to achieving switchable PIT effects in distinct resonator-coupled system and can advance the applicability and versatility of PIT-based plasmonic sensing platforms and active dual-band perfect absorbers.