Monocamadas SnxPy:um novo tipo de materiais bidimensionais com alta estabilidade, mobilidade do portador e propriedades magnéticas

Resumo

A pesquisa de materiais bidimensionais (2D) do grupo V com ferromagnetismo, anisotropia elástica e mobilidade de portadores e estrutura de banda ajustável é uma chave para o desenvolvimento de nanodispositivos em constante desenvolvimento. As monocamadas 2D Sn _x P _y com x / y (1/1, 1/2, 1/3 e assim por diante) número de coordenação são estudados com base na técnica de otimização de enxame de partículas combinada com a otimização da teoria funcional da densidade. Sua estabilidade térmica pode ser confirmada pela dinâmica molecular em 70K e 300K, indicando que os novos materiais 2D têm uma existência estável. As estruturas de banda eletrônica de quatro estruturas estáveis ​​sugerem que todas as monocamadas de Sn _x P _y são semicondutores de lacunas de banda sintonizáveis ​​totalmente ajustáveis ​​e flexíveis sob a tensão biaxial. A monocamada de P \ (\ overline {4} {2} _1 \) m-SnP ₂ com estrutura de banda de valência única pode ir de não magnética a ferromagnética pela dopagem do buraco por causa do "critério de Stoner" e Pmc2 ₁ -SnP ₂ é um semicondutor de gap semelhante ao direto com anisotropia elástica no plano para possuir uma alta mobilidade de elétrons de até 800 cm ² V ⁻¹ s ⁻¹ ao longo do k _b direção, que é muito maior do que MoS ₂ (∼ 200 cm ² V ⁻¹ s ⁻¹ ) O pico de absorção óptica do material está na região do ultravioleta. Essas descobertas expandem as aplicações potenciais do campo emergente de 2D Sn _x P _y estruturas em nanoeletrônica.

Introdução

Compostos binários bidimensionais (2D) têm atraído muita atenção nos últimos anos devido às suas propriedades únicas e podem fornecer orientação confiável para suas aplicações potenciais em nanoeletrônica e dispositivos optoeletrônicos [1]. Por exemplo, o grafeno atraiu grande interesse desde a sua descoberta devido às propriedades e aplicações potenciais [2,3,4,5,6], enquanto o grafeno tem um pequeno gap indetectável em temperatura ambiente, tornando-o difícil de usar em nanodispositivos optoeletrônicos. Portanto, essas dificuldades levaram os pesquisadores a resolverem encontrar materiais 2D com um band gap ideal. Nos anos seguintes, nitreto de boro (BN) [7], MoS ₂ ou outros dichalcogenetos de metais de transição [8,9,10,11,12,13] e trichalcogênicos de metais de transição [14, 15], entre outros estão surgindo. Nos últimos anos, o grafeno e outros materiais 2D do grupo IV (silicone, estaneno e germaneno [16]) tiveram um bom progresso na pesquisa científica. Exceto, materiais semicondutores 2D pertencentes ao grupo V, especialmente fosforeno [17,18,19] e arseneno [20], estão emergindo como uma nova geração de contendores no campo de dispositivos optoeletrônicos. O Fosfeno tem amplas possibilidades de aplicação em transistores de efeito de campo, dispositivos optoeletrônicos, spintrônica, sensores de gás e células solares e assim por diante, enquanto o estaneno, uma estrutura semelhante a um favo de mel 2D, é considerado um novo tipo de material com propriedades físicas superiores após o grafeno devido ao seu forte acoplamento elétron spin-orbital.

É urgente sintetizar dois tipos de elementos para obter novos materiais 2D multifuncionais. É relatado que a liga é frequentemente usada para melhorar as propriedades de materiais 2D para expandir sua aplicabilidade. Por exemplo, 2D MoS _2x Se _{2 (1 - x )} e WS _2x Se _{2 (1 - x )} nanofolhas [21, 22] testemunham propriedades estranhas como eletrônica sintonizável, propriedades ópticas e coeficiente de Poisson negativo no plano com x / y (1/1, 1/2, 1/3 e assim por diante) número de coordenação. Para outro exemplo, material de liga 2D Si _x C _y [23], B _x C _y [24], e B _x Si _y [25] mostram muitas características novas (estrutura ultramoderna, propriedades eletrônicas e mecânicas) pelo cálculo dos primeiros princípios que são diferentes daqueles do estado fundamental puro. Como as monocamadas de fosforeno e estaneno 2D têm propriedades novas, os elementos Sn e P foram compostos com várias estequiometrias.

Neste trabalho, construímos algumas estruturas pelo algoritmo de otimização por enxame de partículas (PSO). Em seguida, selecionamos as quatro estruturas mais estáveis ​​de 2D Sn _x P _y monocamadas com diferentes números de coordenação e investigou as propriedades eletrônicas com base na otimização da teoria funcional da densidade (DFT). As estruturas de banda eletrônica calculadas sugerem que todas as monocamadas estáveis ​​ou metaestáveis ​​com diferentes números de coordenação são semicondutores com um gap indireto. Mais importante, o Pmc2 ₁ -SnP ₂ monocamada é um semicondutor de gap tipo direto com um gap finito de 0,92 eV na região de luz infravermelha. Mas, além disso, o Pmc2 ₁ -SnP ₂ estrutura é um semicondutor de gap semelhante ao direto que possui alta mobilidade de elétrons de ∼ 800 cm ² V ⁻¹ s ⁻¹ , que é muito maior do que o MoS ₂ (∼ 200 cm ² V ⁻¹ s ⁻¹ ) A monocamada de P \ (\ overline {4} {2} _1 \) m-SnP ₂ estrutura com uma estrutura de banda de valência única pode ir de não magnética a ferromagnética pela dopagem do buraco devido ao "critério de Stoner". As estruturas de banda eletrônica calculadas sugerem que todas as monocamadas de Sn _x P _y são semicondutores com lacunas de banda ajustável de forma flexível sob a deformação biaxial, permitindo a engenharia de deformação de quatro lacunas de banda de estruturas dentro de quase toda a faixa de luz visível.

Métodos Computacionais

A fim de garantir uma busca minuciosa da diversidade estrutural, vários x e y selecionar de um a seis são levados em consideração com base no algoritmo de otimização de enxame de partículas (PSO) [26]. Os resultados da pesquisa entregues nas estruturas de monocamada são relativamente constantes apenas para y / x ≧ 1.

Para estudar a estrutura eletrônica de 2D Sn _x P _y monocamadas com número de coordenação diferente, nossos cálculos foram realizados usando o método da teoria funcional da densidade de onda plana (DFT) [27, 28] para realizar no Vienna Ab-initio Simulation Package (VASP) [29,30,31]. Através da Aproximação de Gradiente Generalizado (GGA) para descrever a energia de correlação de troca na forma de Per-dew-Burke-Ernzerhof (PBE) [32,33,34,35] e o potencial elétron-íon é descrito pela amplificação de projeção método de onda [33]. A energia de corte da onda plana foi escolhida como sendo 500 eV de energia para Sn _x P _y sistemas, respectivamente. Um ponto k suficientemente denso (9 × 9 × 1) do espaço recíproco foi amostrado na zona de Brillouin. O espaço de vácuo perpendicular ao plano entre as supercélulas vizinhas é maior que 25 Å, eliminando a interação entre as replicações. No cálculo de duas etapas consecutivas, é definido como 10 ⁵ eV como o valor de convergência de energia. Durante a otimização geométrica, as forças atômicas de todas as estruturas são menores que 0,02 eV Å ⁻¹ usando o método do gradiente conjugado até que os átomos atinjam sua posição ideal. Além disso, usaremos a supercélula com 4 × 4 × 1 para cálculo de dinâmica molecular ab initio (AIMD) quando o algoritmo Nosé [36] em 300K.

A mobilidade da portadora é afetada principalmente pelo espalhamento de onda lateral acústica, espalhamento de onda lateral óptica e espalhamento de impureza ionizada. Como os dois últimos não são tão influentes quanto o primeiro, a mobilidade que calculamos inclui a mobilidade sob o espalhamento de onda lateral acústica. A mobilidade afeta principalmente dois desempenhos dos transistores:Um é que a concentração da portadora em conjunto determina a condutividade (o inverso da resistividade) do material semicondutor. Em segundo lugar, afeta a frequência de trabalho do dispositivo. A principal limitação das características de resposta em frequência dos transistores bipolares é o tempo para as portadoras minoritárias cruzarem a região da base. A mobilidade é um parâmetro importante para medir a condutividade de materiais semicondutores 2D. Ele determina a condutividade dos materiais semicondutores e afeta a velocidade de trabalho dos dispositivos. Assim, a mobilidade da portadora é controlada pela dispersão de fônons e pode ser descrita pela teoria do potencial de deformação (DP) proposta por Bardeen e Shockley [37]. Assim, a mobilidade do portador em materiais 2D pode ser expressa como [38, 39]
$$ {\ mu} _ {2D} =\ frac {2e {\ mathrm {\ hslash}} ^ 3 {C} ^ {2D}} {3 {k} _BT {\ left | {m} ^ {\ ast } \ right |} ^ 2 {E} _1 ^ 2} $$
onde e , ℏ e k _B são a carga do elétron reduzida de Planck e constante de Boltzmann, respectivamente. E T é a temperatura definida para 300K. Onde m * é a massa efetiva, E ₁ é o potencial de deformação constante, e C ^2D é a rigidez no plano.

O efeito linear do sistema no campo de luz sob o vetor de onda pequena é determinado pela parte imaginária da constante dielétrica complexa e a função dielétrica que pode ser calculada por
$$ \ upvarepsilon \ left (\ omega \ right) ={\ varejpsilon} _1 \ left (\ omega \ right) + i {\ varejpsilon} _2 \ left (\ omega \ right) $$
onde o ε ₁ ( ω ) e ε ₂ ( ω ) são a parte real da função e a parte imaginária, ε ₁ ( ω ) pode derivar da parte imaginária ε ₂ ( ω ) a função dielétrica por Kramer – Kronig pode ser expressa [40]. A parte imaginária da função dielétrica pode ser expressa como
$$ {\ varejpsilon} _2 \ left (\ omega \ right) =\ frac {4 {\ pi} ^ 2} {m ^ 2 - {\ omega} ^ 2} \ sum \ limits_ {V, C} \ underset {BZ} {\ int} {d} ^ 3k \ frac {2} {2 \ pi} {\ left | e \ bullet {M} _ {cv} \ right |} ^ 2 \ times \ updelta \ left [{ E} _C \ right. (K) - {E} _V (k) - \ mathrm {\ hslash} \ left. \ Omega \ right] $$
Além disso, o coeficiente de absorção I ( ω ) foi obtido por
$$ I \ left (\ omega \ right) =\ sqrt {2} \ omega \ left [\ sqrt {\ varepsilon_1 ^ 2 \ left (\ omega \ right) - {\ varejpsilon} _2 ^ 2 \ left (\ omega \ right)} - ​​{\ varepsilon} _1 \ left (\ omega \ right) \ right] 1/2 $$
onde o C é a banda de condução, o V são os estados da banda de valência, Ω é o volume da célula unitária, m é a massa dos elétrons livres, e é a carga dos elétrons livres, e ω é a frequência dos fótons incidentes.

Resultados e discussão

Estabilidade

Primeiro, quatro 2D Sn _x P _y monocamadas foram consideradas para determinar suas estabilidades energéticas. A energia de formação é um parâmetro de energia em um sistema termodinâmico que é um ponto chave para verificar a estabilidade do sistema. A estabilidade relativa de Sn _x P _y monocamadas podem ser confirmadas calculando a energia de formação e é calculada como
$$ {E} _ {\ mathrm {form}} =\ left ({E} _ {\ mathrm {total}} - {N} _ {\ mathrm {Sn}} {E} _ {\ mathrm {Sn} } - {N} _ {\ mathrm {P}} {E} _P \ right) / \ left ({N} _ {\ mathrm {Sn}} + {N} _ {\ mathrm {p}} \ right) $$
onde E é a energia de um composto ou elemento constituinte a uma pressão específica. N é o número de átomos na célula unitária. A energia de formação negativa do sistema calculado indica que a configuração é estável ou metaestável [41]. As energias de formação calculadas de Sn _x P _y as monocamadas são - 0,235, - 0,223, - 0,159 e - 0,016 eV / átomo (mostrado na Tabela 1), respectivamente. De acordo com sua definição, um valor menor indica maior estabilidade. Obviamente, P \ (\ overline {6} \) m2-SnP é a mais estável dessas quatro estruturas. Mais particularmente, a alta estabilidade térmica de materiais semicondutores é particularmente importante na aplicação de dispositivos eletrônicos. Aqui, a estabilidade térmica do Sn _x P _y monocamadas examinadas usando simulações de dinâmica molecular ab initio (AIMD). Com base nas simetrias dos grupos de espaço, calculamos apenas a estabilidade de P \ (\ overline {6} \) m2-SnP para estruturas semelhantes P \ (\ overline {6} \) m2-SnP e Pmc2 ₁ -SnP ₂ e Pmc2 ₁ -SnP ₂ para Pmc2 ₁ -SnP ₂ e P \ (\ overline {4} {2} _1 \) m-SnP ₂ estruturas. Os resultados indicam que o valor médio da energia total da estrutura permanece quase inalterado, e a estrutura permanece inalterada após 1 ps, 3 ps e 5 ps, sugere que Sn _x P _y as monocamadas são termicamente estáveis ​​(na Figura S1). Em seguida, calculamos as curvas de dispersão de fônons e não temos frequências vibracionais imaginárias, o que implica que as estruturas são dinamicamente estáveis ​​(na Figura S1). Vários métodos têm sido relatados na literatura para sintetizar materiais em camadas, incluindo clivagem micromecânica [2], crescimento epitaxial [42], deposição de vapor químico [43] e esfoliação líquida [44]. Alguns materiais com estrutura semelhante foram preparados experimentalmente com sucesso. Encontramos alguns relatórios relacionados que poucas nanofolhas de camada GaSe foram transformadas em um fotodetector de alto desempenho no experimento [45]. Além disso, a preparação, o isolamento e a caracterização inequívoca rápida de camadas ultrafinas de tamanho grande de MoS ₂ , GaS e GaSe depositados em SiO ₂ / Si substratos são relatados [46].

Conforme plotado na Fig. 1a, b, as estruturas de P \ (\ overline {3} \) m1-SnP exibem uma estrutura semelhante à fase hexagonal P \ (\ overline {6} \) m2-SnP. O Pmc2 ₁ -Sn P ₂ fase trigonal (Fig. 1c) exibe que o x / y a composição é ainda aumentada para 1/2. O material de uma estrutura semelhante a P \ (\ overline {4} \) 2 ₁ m-SnP ₂ provou-se estável por cálculo teórico [47]. Além disso, um novo estudo encontra a estrutura de XY ₂ (Fig. 1d) é um semicondutor bandgap indireto e pode ser suscetível a campo elétrico e estresse. Acreditamos que o material que prevemos terá uma preparação bem-sucedida no futuro com o desenvolvimento de tecnologia.

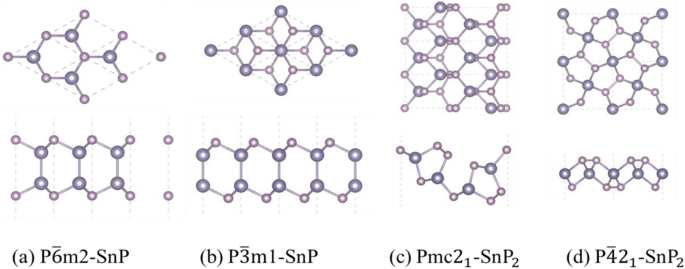
Vistas superior e lateral das estruturas atômicas de Sn _x P _y monocamadas: a P \ (\ overline {6} \) m2-SnP, b P \ (\ overline {3} \) m1-SnP, c Pmc2 ₁ -SnP ₂ , e d P \ (\ overline {4} {2} _1 \) m-SnP ₂ ; o nível de Fermi (linha tracejada horizontal) é deslocado para 0 eV. As esferas rosa pesadas representam átomos de Sn e as esferas rosa claro representam átomos P

Propriedades eletrônicas e magnéticas

As estruturas de banda computadas e densidade parcial dos estados de Sn _x P _y as monocamadas são plotadas na Fig. 2. Conforme mostrado na Fig. 2a, o P6̅m2-SnP é um semicondutor indireto com um gap de banda de 1,19 eV. A banda de valência máxima (VBM) na direção Γ → K é contribuída pelos orbitais hibridizados Sn-p e P-p, enquanto a banda de condução mínima (CBM) no ponto K deriva dos orbitais hibridizados Sn-s e P-p. P \ (\ overline {3} \) m1-SnP exibe estruturas de banda eletrônica semelhantes à contraparte P \ (\ overline {6} \) m2-SnP, mas com um gap menor de 1,21 eV. A dispersão da banda de valência de P \ (\ overline {6} \) m2-SnP e P \ (\ overline {3} \) m1-SnP perto do ponto Γ e nível de Fermi ( E _F ) é bastante plano, dada a alta densidade de estados (DOS) e uma singularidade de van Hove em torno do VBM. O Pmc2 ₁ -SnP ₂ exibe um caráter semicondutor de lacuna semelhante a direta ( E _g (direto) - E _g (indireto) =6 meV) com uma lacuna de banda de 0,72 eV (ver Fig. 2c). Seu VBM é atribuído principalmente aos orbitais P-p, enquanto seu CBM é principalmente contribuído por orbitais P-p e orbitais Sn-s. O P \ (\ overline {4} {2} _1 \) m -SnP ₂ é um semicondutor de lacuna indireta com um E _g de 1,79 eV, e as bandas derivam de é semelhante à Fig. 2c. Mais importante ainda, P \ (\ overline {4} {2} _1 \) m-SnP ₂ monocamada tem uma condição semelhante comparada com a Fig. 2a, b, um caráter de dispersão de banda plana em torno do VBM também surge, resultando em DOS muito alto e uma singularidade de van Hove.

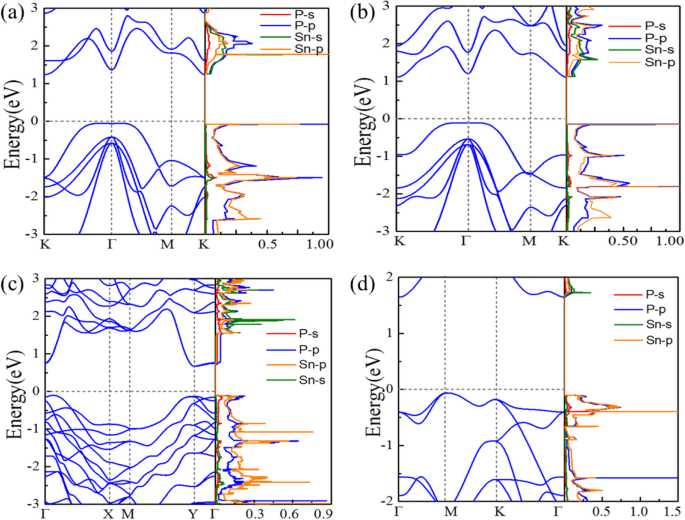
Estruturas de banda eletrônica computadas e densidade parcial de estados do VBM e CBM de Sn _x P _y monocamadas: a P \ (\ overline {6} \) m2-SnP, b P \ (\ overline {3} \) m1-SnP, c Pmc2 ₁ -SnP ₂ , e d P \ (\ overline {4} {2} _1 \) m-SnP ₂

De acordo com o critério de Stoner, o ferromagnetismo espontâneo ocorre se a energia cinética for menor do que a energia de divisão de troca, que é se o DOS em E _F é alto o suficiente. A Figura 2d mostra o DOS muito alto em torno do VBM; o P \ (\ overline {4} {2} _1 \) m-SnP ₂ pode satisfazer o critério de Stoner se for E _F é deslocado para uma posição com alto DOS através de dopagem de orifícios. Conforme mostrado na Fig. 3a, a dopagem de orifícios pode introduzir momentos magnéticos em concentrações de dopagem apropriadas. Como esperado, o resultado do cálculo sugere que o P \ (\ overline {4} {2} _1 \) m-SnP ₂ pode ser convertido em um estado fundamental ferromagnético além da densidade crítica do furo. Entre eles, a densidade do furo n _h pode ser expresso como n _h = m _h / S _célula , onde S _célula e m _h são a área da célula primitiva e o número de orifícios introduzidos na célula primitiva. A injeção do orifício na monocamada P \ (\ overline {4} {2} _1 \) m-SnP ₂ na verdade, leva ao ferromagnetismo. O momento magnético exibe uma relação semelhante a um pico íngreme com a densidade do furo. Como um momento de rotação apreciável é induzido pela dopagem de orifícios no sistema, a estrutura da banda de energia em torno do nível de Fermi mudou muito devido à divisão de rotação. Particularmente, a estrutura de banda polarizada por spin (mostrada na Fig. 3b) de P \ (\ overline {4} {2} _1 \) m-SnP ₂ em 7,2 × 10 ¹⁴ cm ⁻² mostra que a monocamada se torna um meio metal perfeito. Portanto, prevemos que o estado FM estável com meia metalicidade pode ser realizado no P \ (\ overline {4} {2} _1 \) m-SnP ₂ monocamada.

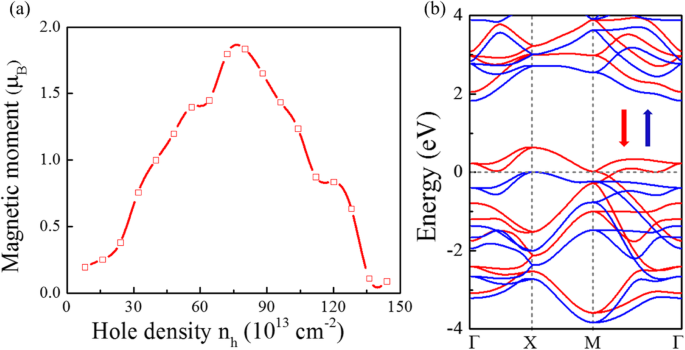
Ferromagnetismo em P \ (\ overline {4} {2} _1 \) m-SnP ₂ monocamada. ( a ) Momentos de rotação vs densidade do furo n _h . b Estrutura de banda de valência calculada de P \ (\ overline {4} {2} _1 \) m-SnP ₂ em n _h =7,2 × 10 ¹⁴ cm ⁻² . As bandas de spin-up e spin-down são mostradas em azul e vermelho, respectivamente. O nível de Fermi é definido como 0 eV

Anisotropia elástica e mobilidade da portadora de monocamada

Os efeitos de deformação nas propriedades eletrônicas das monocamadas 2D Sn _x P _y estruturas também são interessantes. A Figura 4a apresenta a variação do gap de energia sob deformação biaxial ε . A lacuna de energia de Sn _x P _y as monocamadas são marcadamente moduladas de acordo com algumas regras. Por exemplo, a lacuna de energia de P \ (\ overline {6} \) m2-SnP diminui de 1,19 para 0,52 eV com o aumento da deformação de tração até ε =8%, primeiro aumentando de 1,12 para 1,36 eV para ε 2%, diminuindo de 1,36 para 0,51 eV. Além disso, uma vez que o a e b do parâmetro de rede do Pmc2 ₁ -SnP ₂ estrutura são diferentes, as mudanças das propriedades eletrônicas são diferentes ao longo do x -eixo e y -eixo [48], como mostrado na Fig. 4b. É óbvio que quando a tensão uniaxial é aplicada em diferentes direções, a mudança no x direção é diferente da mudança no y direção. Considerando a gama de lacunas de energia com a deformação ε , a faixa de lacuna de banda ajustável por deformação no plano cobre quase toda a região de luz visível com base no cálculo de primeiros princípios.

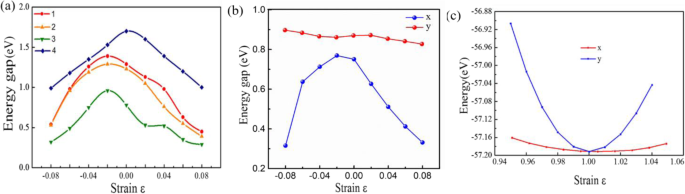
Propriedades eletrônicas de estruturas dependentes de deformação:(1) P \ (\ overline {6} \) m2-SnP, (2) P \ (\ overline {3} \) m1-SnP, (3) Pmc2 ₁ -SnP ₂ , e (4) P \ (\ overline {4} {2} _1 \) m-SnP ₂ . b Propriedades eletrônicas dependentes da cepa uniaxial de Pmc2 ₁ -SnP ₂ . c Energia do Pmc2 ₁ -SnP ₂ monocamada vs coloração uniaxial

Além disso, também investigamos o efeito do estresse uniaxial, conforme mostrado na Fig. 4c. A rigidez no plano C ^2D ( C ^2D =[∂ ² E / ∂ δ ² ] / S ₀ , onde S ₀ é a área de 2D Pmc2 ₁ -SnP ₂ monocamada) podem ser obtidos ajustando a parábola. Curiosamente, a rigidez no plano C ^2D mostrando anisotropia elástica extremamente óbvia ao longo de a e b as direções são calculadas em 12,1 e 105,6 N / m, respectivamente. Porque o Pmc2 ₁ -SnP ₂ exibe um caráter semicondutor de lacuna semelhante ao direto, as massas efetivas ( m ^∗ = ℏ ² ( ∂ ² E / ∂K ² ) ⁻¹ ) de elétrons ( m _e é | m ^* _e |) e orifícios ( m _h é | m ^* _h |) associado ao semicondutor (quase) direto Pmc2 ₁ -SnP ₂ monocamada também são calculadas. As massas efetivas são listadas (Tabela 2). O mais interessante é a massa efetiva dos elétrons no k _b direção (0,15 me) é muito menor do que no k _a direção (1,31 me), indicando a fácil deriva dos elétrons no k _b direção. Há outro parâmetro importante é a constante DP E ₁ ( E ₁ =d E _borda / d δ ) para elétrons ao longo de a e b as direções são calculadas em 5,36 e 11,57 eV, respectivamente. Surpreendentemente, a portadora calculada pode ser alcançada em aproximadamente 800 cm ² V ⁻¹ s ⁻¹ no k _b direção. Como comparação, a mobilidade da portadora do MoS ₂ monocamada é ∼ 200 cm ² V ⁻¹ s ⁻¹ em experimentos [8]. No entanto, a mobilidade da portadora é de aproximadamente ∼ 8 cm ² V ⁻¹ s ⁻¹ no k _a direção. Portanto, a alta mobilidade de portadores encontrada neste estudo é de grande significância para o estudo do transporte de elétrons.

Propriedade óptica

As propriedades fotoelétricas dos materiais fotoeletrônicos são caracterizadas pela função dielétrica, fotocondutividade e coeficiente de absorção. As partes imaginárias da função dielétrica são mostradas na Fig. 5a. Observe que Pmc2 ₁ -SnP ₂ a monocamada mostra a absorção começando em ± 0,70 eV, e aparecem três picos de absorção principais em ± 0,9, ~ 3,2 e ± 4,0 eV. Conforme ilustrado na Fig. 5b, mostra a absorbância em todas as três direções na faixa visível e faixa ultravioleta para monocamada Pmc2 ₁ -SnP ₂ . Então, Pmc2 ₁ -SnP ₂ materiais de monocamada podem ser usados ​​para fotodetectores cegos solares atomicamente finos para, por exemplo, detecção eficiente de chamas.

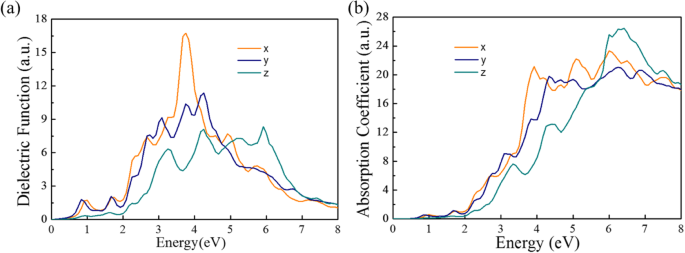
a Funções dielétricas computadas versus energia para Pmc2 ₁ -SnP ₂ ao longo de diferentes direções de luz incidente. b Coeficiente de absorção imaginário calculado

Conclusões

Em conclusão, com base nos algoritmos PSO combinados com cálculos de primeiros princípios, identificamos vários 2D Sn _x P _y monocamadas com as razões de x / y =1:1 e 1:2. Surpreendentemente, essas novas monocamadas também possuem propriedades eletrônicas e magnéticas peculiares:a monocamada de P \ (\ overline {4} {2} _1 \) m-SnP ₂ estrutura com estrutura de banda de valência única pode ir de não magnética a ferromagnética pelo dopagem do furo devido ao “critério de Stoner”; o Pmc2 ₁ -SnP ₂ estrutura é um semicondutor de lacuna semelhante a direta com anisotropia elástica no plano que possui alta mobilidade de elétrons de até 800 cm ² V ⁻¹ s ⁻¹ ao longo do k _b direção, que é muito maior do que MoS ₂ (∼ 200 cm ² V ⁻¹ s ⁻¹ ) O pico de absorção óptica do material está na região do ultravioleta. Essas descobertas expandem as aplicações potenciais do campo emergente de 2D Sn _x P _y estruturas em nanoeletrônica. Estas propriedades desejáveis ​​do multifuncional Sn _x P _y monocamadas fornecem grandes aplicações promissoras em eletrônica e optoeletrônica.

Disponibilidade de dados e materiais

Eles estão todos no texto principal e nas figuras.

Estudos comparativos em nanofolhas bidimensionais retangulares e hexagonais de dióxido de molibdênio com espessuras diferentes Dosagem conjunta de ozônio e água desionizada como precursores oxidantes do crescimento de película fina de ZnO por deposição de camada atômica