Defeito e doping Penta-grafeno projetado para catálise da reação de evolução de hidrogênio

Resumo

A eletrólise da água é um método sustentável e limpo para produzir hidrogênio combustível via reação de evolução de hidrogênio (HER). O uso de eletrocatalisadores estáveis, eficazes e de baixo custo para HER para substituir metais nobres caros é altamente desejado. Neste artigo, usando o cálculo de primeiros princípios, projetamos um defeito e penta-grafeno dopado com N-, S-, P (PG) como um eletrocatalisador bidimensional (2D) para HER, e sua estabilidade, propriedades eletrônicas e o desempenho catalítico foi investigado. A energia livre de Gibbs (Δ G _H ), que é o melhor descritor para o HER, é calculado e otimizado, os resultados do cálculo mostram que o Δ G _H pode ser 0 eV com vacâncias C2 e dopagem P em sítios ativos C1, que deve ser o desempenho ideal para um catalisador HER. Além disso, revelamos que quanto maior a transferência de carga de PG para H, mais próximo Δ G _H é zero de acordo com o cálculo das diferenças de densidade de carga do elétron e a análise de cargas de Bader. Posteriormente, demonstramos que o desempenho de HER prefere o mecanismo de Volmer-Heyrovsky neste estudo.

Histórico

Devido às mudanças climáticas e à poluição ambiental causada pelo uso de combustíveis fósseis, a exploração e a utilização de energia limpa e renovável são o meio termo depois dos dias de hoje [1,2,3,4]. Como uma fonte de energia limpa, renovável e ecologicamente correta, o hidrogênio (H ₂ ) tem atraído atenção considerável para atender às necessidades futuras de energia humana [5, 6]. A eletrólise da água é um método sustentável e limpo para produzir H ₂ , e os eletrocatalisadores podem aumentar a eficiência da divisão da água de forma observável [7, 8]. Para a reação de evolução de hidrogênio (HER), os nanomateriais à base de platina são considerados os melhores eletrocatalisadores por causa de uma pequena inclinação de Tafel, um baixo potencial excessivo, uma energia livre de Gibbs ligeiramente negativa (Δ G _H ) e uma alta densidade de corrente de troca [9, 10], mas a escassez e o alto custo dificultam suas aplicações em escala industrial [11]. Portanto, o desenvolvimento de eletrocatalisadores eficazes, abundantes em terra e de baixo custo é essencial para HER [12,13,14].

Na verdade, uma ampla gama de eletrocatalisadores abundantes em terra foram estudados e projetados para HER [15,16,17]. Entre esses materiais, nanomateriais bidimensionais (2D) fornecem novas oportunidades para HER por causa das propriedades estruturais e eletrônicas atraentes. Até o momento, os dichalcogenetos de metais de transição (TMDs) e os materiais à base de grafeno são os maiores e mais intensamente estudados grupos de eletrocatalisadores 2D para HER [18,19,20,21,22,23]. Os catalisadores TMDs HER têm baixo sobrepotencial e pequena inclinação Tafel, propriedades eletrônicas incomuns e alta estabilidade do ar, exibem alto desempenho HER, e diferentes métodos foram usados para melhorar seu desempenho catalítico [24, 25]. Os catalisadores HER à base de grafeno têm atraído considerável atenção e estudos persistentes por causa de seus méritos estruturais distintos, como alta condutividade elétrica, grande área de superfície e boa estabilidade química [26, 27]. Muitos métodos foram usados para aumentar a atividade catalítica, como dopagem de heteroátomo e engenharia de defecção [28, 29]. Enquanto isso, a pesquisa intensiva em outros novos alótropos de carbono 2D também foram desenvolvidos, como graphdiyne [30] e penta-grafeno (PG) [31]. Como um alótropo de carbono 2D, o PG é composto apenas de pentágonos de carbono e herda muitas propriedades excepcionais de materiais 2D, como band gap eletrônico finito, locais ativos abundantes e grande área de superfície, portanto, prevê-se que seja um material versátil para muito potencial aplicações como outros materiais baseados em grafeno 2D [32,33,34,35]. Uma vez que existem apenas aplicações na adsorção de gás [36,37,38], H ₂ armazenamento [39, 40], materiais de ânodo no momento [41, 42], nenhum relatório foi encontrado sobre a aplicação no HER. Portanto, a pesquisa sobre HER por PG é de grande importância e não só preenche essa lacuna, mas também amplia o escopo dos catalisadores HER à base de grafeno. No entanto, o PG puro é considerado inerte para o HER com um Δ G relativamente grande _H , o que significa que a adsorção de hidrogênio é difícil e inibe o HER. Isso é semelhante aos problemas encontrados pelo grafeno puro (Δ G _H =1,85 eV [43]). A dopagem de heteroátomos em materiais à base de grafeno pode ajustar suas propriedades eletrônicas e catalíticas, o que os torna potenciais catalisadores para as aplicações práticas [3]. Portanto, conseguimos adequar a atividade catalítica de PG por dopagem de heteroátomo [44,45,46] e engenharia de deserção [47, 48].

Neste artigo, usando cálculos de primeiros princípios, projetamos e demonstramos um defeito e PG dopado com N-, S-, P e investigamos sua estabilidade e propriedades eletrônicas e avaliamos seu desempenho como eletrocatalisadores HER. Nossos resultados revelam que o defeito e o PG dopado podem obviamente aumentar a atividade catalítica em direção a HER, em comparação com o PG puro. Também é mostrado que o Δ G _H pode ser 0 eV com vacâncias C2 e dopagem P em sítios ativos C1, que deve ser o desempenho ideal para um catalisador HER, então PG dopado com P tem o Δ G ideal _H e barreira de energia de ativação para a etapa de determinação de taxa entre as três contrapartes, e exibe um desempenho mais favorável. Mostramos ainda que a atividade catalítica surge a partir dos átomos de dopagem incorporados, os quais podem fornecer via eficiente para o transporte de carga durante a eletrólise, resultando na redução em Δ G _H . Também demonstramos que o mecanismo de Volmer-Heyrovsky é mais preferido para HER em defeito e PG dopado. Comparamos nossos resultados com os de outros pesquisadores sobre grafeno, e pode-se constatar que a engenharia de defecção e dopagem são mais eficazes para PG na catálise de HER. Assim, nosso esforço em defeitos e PG dopado o torna um eletrocatalisador altamente promissor para HER, e nossas descobertas fornecem uma compreensão profunda no projeto de eletrocatalisadores eficientes e duráveis. Este método também pode ser aplicado a outros materiais à base de grafeno.

Métodos Computacionais

Nossos cálculos de primeiros princípios foram realizados usando o Vienna Ab initio Simulation Package (VASP) [49]. Os potenciais de onda aumentada projetada (PAW) foram usados para analisar as interações entre os elétrons do núcleo e os elétrons de valência [50,51,52]. As interações de correlação de troca de elétrons foram descritas usando o funcional Perdew-Burke-Ernzerhof (PBE) dentro da aproximação de gradiente generalizado (GGA) [53]. O funcional de correlação de troca DFT-D3 foi introduzido na otimização estrutural para levar em consideração a interação de van der Waals. O espaço de vácuo ao longo do z -direction foi definido para 20 Å a fim de eliminar as interações entre PG e suas imagens periódicas.

O corte de energia das ondas planas foi definido como 500 eV. O critério de convergência foi definido como 10 ⁻⁵ eV para uma energia total. Todas as posições atômicas e estruturas de rede foram totalmente relaxadas com o limite de uma força máxima de 0,02 eV Å ⁻¹ . A fim de garantir a precisão e eficiência do cálculo, uma malha de k-pontos centrada em gama com um método de Monkhorst-Pack 5 × 5 × 1 foi empregada para todas as estruturas consideradas após o teste de convergência [54]. A quantidade de transferência de carga entre os átomos de C e átomos de H foi calculada usando o código de Bader [55]. Também calculamos as barreiras de energia de adsorção de H * usando o método da banda elástica de escalada com deslocamento de imagem (CI-NEB) [56, 57]. O CI-NEB é um método eficiente para determinar o caminho de energia mínimo e os pontos de sela entre uma determinada posição inicial e final [58,59,60], e em nossos cálculos CI-NEB, as estruturas inicial e final foram totalmente otimizadas.

A energia de adsorção (Δ E _H ) é definido como
$$ \ Delta E _ {{\ text {H}}} =E (* {\ text {H}}) - E (*) - \ frac {1} {2} E ({\ text {H}} _ {2}) $$
onde E (* H) e E (*) são a energia total das estruturas com e sem adsorção de hidrogênio, respectivamente, e E (H ₂ ) é a energia total de um H ₂ molécula.

A energia livre de Gibbs (Δ G _H ) é definido como:
$$ \ Delta G _ {{\ text {H}}} =\ Delta E _ {{\ text {H}}} + \ Delta E _ {{{\ text {ZPE}}}} - T \ Delta S _ {{\ enviar mensagem de texto {H}}} $$
onde Δ E _H é a energia de adsorção, Δ E _ZPE é a diferença na energia do ponto zero, T é a temperatura (298,15 K) e Δ S _H é a diferença de entropia de H adsorvido e H na fase gasosa. Aproximamos a entropia de adsorção de hidrogênio como \ (\ Delta S _ {{\ text {H}}} \ approx \ frac {1} {2} (S _ {{{\ text {H}} _ {2}}} ^ {\ circ}) \), onde \ (S _ {{{\ text {H}} _ {2}}} ^ {\ circ} \) é a entropia da fase gasosa H ₂ em condições padrão, T Δ S _H foi definido como - 0,202 eV após o cálculo neste estudo.

Resultados e discussão

Estrutura e atividade catalítica de defeito e PG dopado

A estrutura otimizada de PG é mostrada na Fig. 1. Para conveniência de discussão, a seguir agrupamos o sp ³⁻ e sp ²⁻ átomos de C hibridizados como C1 e C2, respectivamente. A distância entre C1 e C2 é de 1,55 Å, e o comprimento da ligação C2-C2 é de 1,34 Å, o que é consistente com o resultado experimental [31].

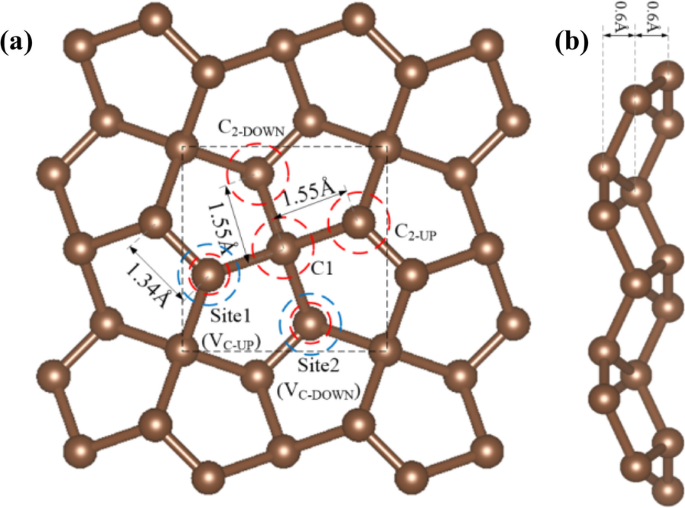
a Superior e b vistas laterais da estrutura otimizada do PG. O retângulo preto tracejado indica célula unitária, os círculos azuis tracejados indicam dois locais de vacância C, os círculos tracejados vermelhos indicam locais de dopagem usados neste artigo

No início, primeiro investigamos os sítios C1 e C2 no plano basal de PG puro para HER, o Δ G calculado _H os valores são 2,43 eV e 2,72 eV, respectivamente. Portanto, nossos cálculos mostram que o PG puro é considerado inerte para o HER com um Δ G relativamente grande _H de H, o que significa que a adsorção de hidrogênio é difícil e HER é inibida. Portanto, conseguimos usar alguns métodos para adequar a atividade catalítica do PG. Pesquisamos os possíveis sítios ativos para dopagem e também investigamos os sítios ativos para C1 e C2 com dopagem N, S, P, respectivamente. Os resultados do cálculo mostram que nenhuma melhoria óbvia de HER pode ser obtida se apenas a engenharia de dopagem foi introduzida. No caso da estrutura dopada com P, o Δ G calculado _H os valores dos locais C1 e C2 são 1,24 eV e 1,40 eV, respectivamente. Posteriormente, investigamos o defeito PG com locais de vacância C. Os resultados do cálculo revelam que a estrutura de vacância C1 não pode melhorar o desempenho de HER, mas a estrutura de vacância C2 pode diminuir Δ G _H obviamente, então usamos a estrutura de vaga C2 neste estudo. As estruturas otimizadas com V _C-UP e V _C-DOWN Os locais de vacâncias C2 são mostrados na Fig. 2, os defeitos de vacância são construídos removendo átomos C2 de C _2-UP ou C _2-DOWN local em uma supercélula de 24 átomos. O Δ G calculado _H os valores são mostrados na Tabela 1, onde C1 e C2 são os sítios ativos para a adsorção de hidrogênio.

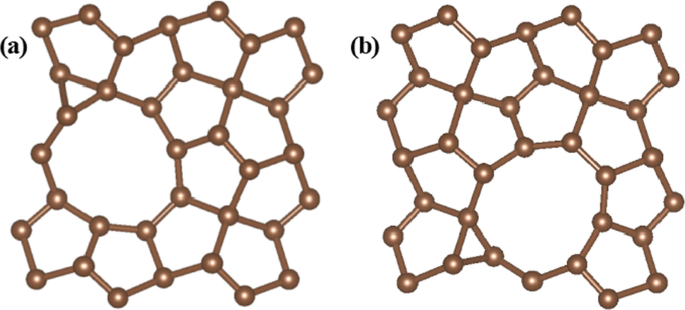
As estruturas otimizadas de PG com dois locais de vacância C2 diferentes. a V _C-UP Local vago C2, b V _C-DOWN Local vago C2

Embora seja confirmado por nossos cálculos que as vacâncias C2 são eficientes para aumentar a atividade HER, PG com estrutura de vacância C2 ainda não é ideal para um catalisador HER. Assim, investigamos o defeito e dopamos PG para HER. Usamos PG com vacância C2 como estrutura inicial, que é mostrado na Fig. 2 e, em seguida, investigamos todos os diferentes sítios ativos possíveis com dopagem N, S, P, incluindo C1, C _2-UP e C _2-DOWN sites. Como resultado, descobrimos que um melhor desempenho de HER poderia ser alcançado com uma combinação de vacância de C2 e dopagem de heteroátomo. Investigamos todas as estruturas possíveis, e os resultados mostraram que existem duas estruturas que podem alcançar um melhor desempenho de HER, uma estrutura é uma combinação de C _2-UP vacância e dopagem de heteroátomo no C _2-DOWN site, e o outro é uma combinação de C _2-DOWN vacância e dopagem de heteroátomo no C _2-UP local. Então, nos concentramos nessas duas estruturas e descobrimos que elas podem deslocar o Δ G _H valores mais próximos de zero. As estruturas otimizadas são mostradas na Fig. 3, e os comprimentos de ligação calculados estão resumidos na Tabela 2.

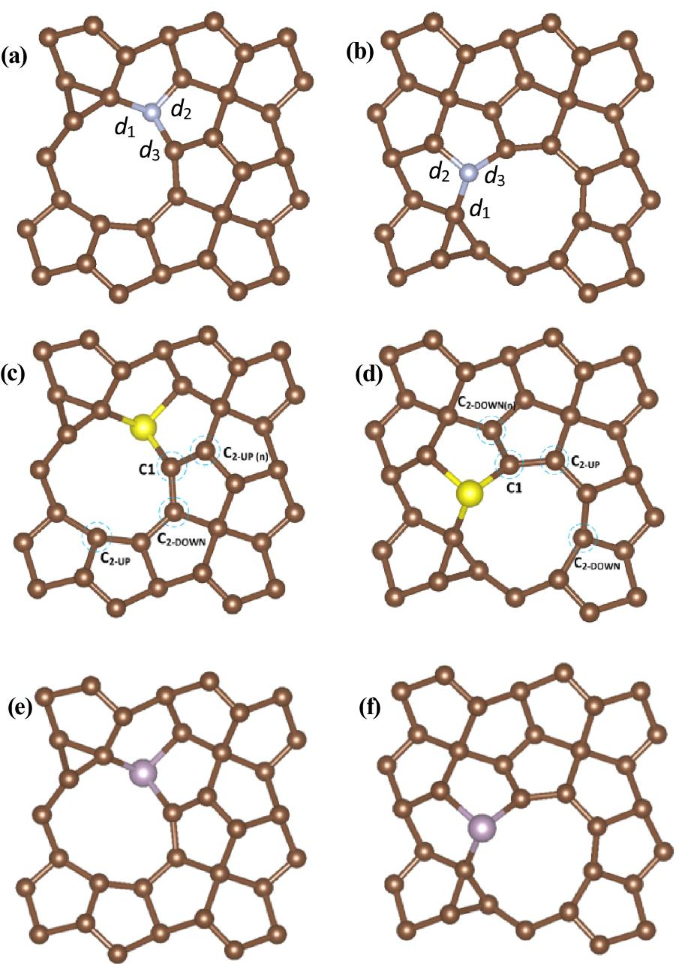
As estruturas otimizadas para o defeito e PG dopado com os dois locais de vacância C2 diferentes, a V _C-UP N-dopado, b V _C-DOWN N-dopado, c V _C-UP S-dopado, d V _C-DOWN S-dopado, e V _C-UP Dopado com P, f V _C-DOWN Dopado com P, os círculos tracejados em azul indicam possíveis locais ativos para a evolução do hidrogênio

Podemos ver que há uma ligeira diferença entre os comprimentos de ligação correspondentes do PG dopado com N e do PG puro. Por causa do grande raio dos átomos S e P, essas duas estruturas sofrem muito mais distorção, mas ambas podem manter a estrutura de PG.

Para investigar a estabilidade de PG com vacância de C2 e dopagem de heteroátomo, calculamos a energia de formação, que é definida como
$$ E _ {{\ text {f}}} =\ left ({E _ {{\ text {t}}} - E _ {{\ text {V}}} + E _ {{\ text {C}}} - E _ {{\ text {d}}} - \ frac {1} {2} \ mu _ {{\ text {H}}}} \ right) $$
onde E _t é a energia total do sistema defeituoso e dopado, e E _V é a energia da vacância C2 PG, E _C é a energia média por átomo de C do PG primitivo, E _d é a energia dos átomos de dopagem, \ (\ mu _ {{\ text {H}}} \) é tirada da energia total do H ₂ molécula, respectivamente. Um de nossos resultados de cálculo sobre as energias de formação das duas estruturas anteriores com sítios ativos C1 para HER é mostrado na Fig. 4. Podemos ver que as energias de formação negativas indicam defeito energeticamente favorável e viável e PG dopado com S, P. Da mesma forma, E _f os valores das estruturas dopadas com N com sítios ativos para HER são todos positivos. Investigamos todos os sítios ativos possíveis e obtivemos resultados semelhantes aos mostrados na Fig. 4, portanto, investigaremos apenas o PG dopado com S e P. De acordo com a definição, um E mais negativo _f valor indica maior estabilidade da estrutura, então PG dopado com P tem excelente estabilidade, bem como bom desempenho de HER.

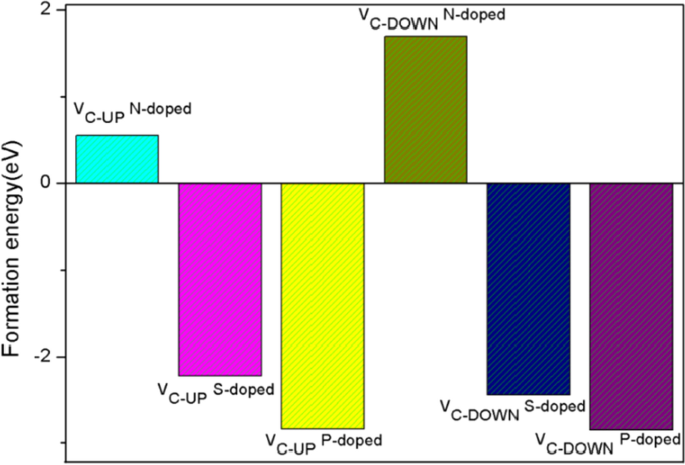
Energia de formação de dois defeitos iniciais e estruturas PG dopadas com sítios ativos C1 para HER, valor mais negativo indica maior estabilidade da estrutura

Origem da atividade catalítica de HER

DOS e estruturas de banda

Para alcançar uma compreensão aprofundada da natureza da vacância de C2 e engenharia de dopagem na atividade de HER, investigamos o DOS total e projetado, a estrutura de banda eletrônica do defeito e o PG dopado com S, P. A Figura 5 é um de nossos resultados de cálculo sobre estruturas de banda eletrônica, DOS total e projetado de PG intocado, V _C-UP , V _C-UP S-dopado e V _C-UP PG dopado com P.

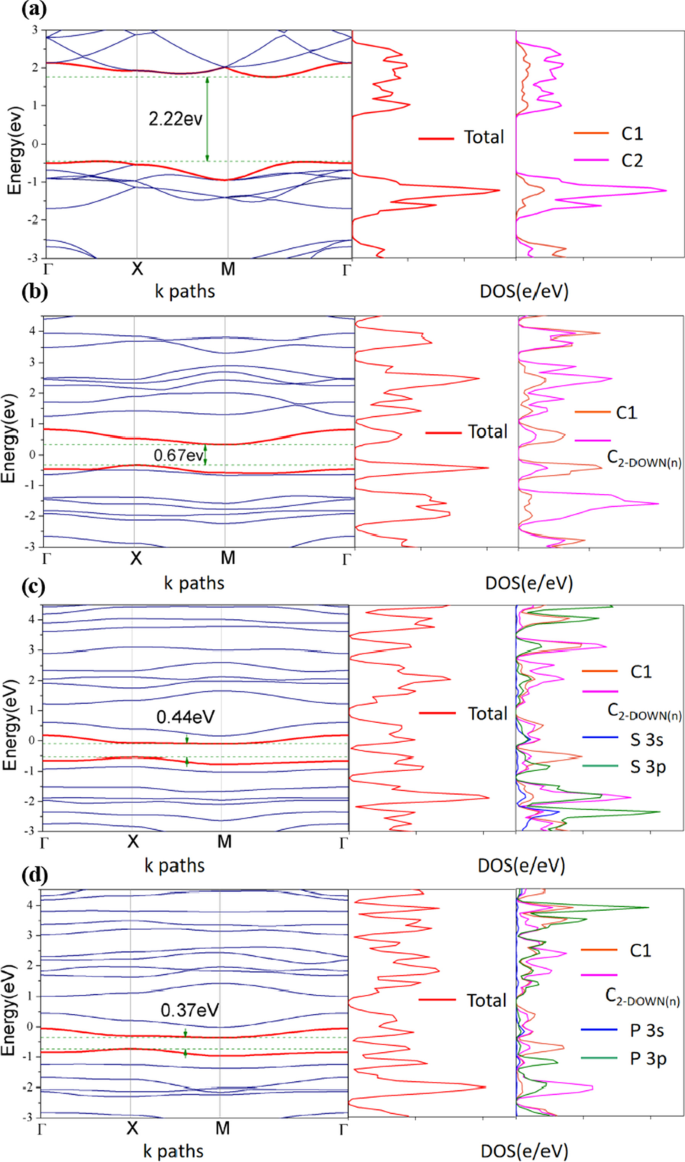
Estrutura de banda eletrônica, DOS total e projetado do defeito e PG dopado. a PG Pristine, b V _C-UP Local vago C2, c V _C-UP S-dopado e d V _C-UP Dopado com P, respectivamente. As estruturas de c e d como mostrado na Fig. 3. Eles são calculados usando PBE funcional, o nível de Fermi é deslocado para 0,00 eV

Pela figura, podemos ver que, quando a vacância C2 é introduzida, alguns novos estados de defeito destacados por curvas vermelhas aparecem na faixa proibida perto do nível de Fermi. Obviamente, esses novos estados surgem da vaga C2. Além disso, quando a dopagem com heteroátomo S, P é introduzida, o gap fica mais estreito (de 2,22 eV [31] para 0,37 eV) e o número de novos estados de defeito próximo ao nível de Fermi aumenta, o que pode possivelmente melhorar a força de adsorção de H *.

No entanto, descobrimos que o DOS de V _C-UP perto do nível de Fermi é muito maior do que o PG puro. Além disso, a densidade de elétrons perto do nível de Fermi de vacância de C2 e PG dopado com S, P é ainda mais aumentada em relação ao PG puro. Também descobrimos que os orbitais S 3p e P 3p sofrem hibridização significativa com os estados C1 e C2, levando a fortes interações entre os heteroátomos e C, e a formação de ligações S – C e P – C. Estes resultados demonstram que a combinação da vacância C2 e dopagem de heteroátomos S, P pode ser uma engenharia melhor para melhorar a atividade de HER.

Diferença de densidade de elétrons e transferência de carga

Além disso, para estudar a interação de ligação entre o átomo de H e PG, calculamos as diferenças de densidade de carga do elétron para o defeito e o PG dopado com S-, P com diferentes sítios ativos para a evolução do hidrogênio. Um de nossos resultados de cálculo sobre a diferença de densidade de carga do elétron e análise de cargas de Bader para um C _2-DOWN vacância e PG dopado com P com H * adsorvido nos diferentes sítios ativos para adsorção de hidrogênio é mostrado na Fig. 6. As cores amarela e azul representam o acúmulo e a redução de carga, respectivamente. É mostrado que os elétrons se acumulam em torno dos átomos de H e se reduzem em torno dos átomos de C que estão ligados aos átomos de H, indicando uma transferência de carga de PG para H *. A transferência de cobrança também é confirmada pela análise de cobranças de Bader. Os resultados do cálculo mostram que há 0,18, 0,04, 0,02 e 0,01 elétrons se transferindo para H * em C1, C _2-DOWN , C _{2-DOWN (n)} e C _2-UP sites, respectivamente. Mostramos ainda que quanto maior a transferência de carga de PG para H *, mais próximo Δ G _H é zero, o que significa o desempenho ideal para um catalisador HER, como mostrado na Fig. 7. Pode ser visto na Fig. 6 que os elétrons são transferidos de PG para H *, resultando no aumento da densidade de carga das ligações, o que significa que a estabilização da espécie H * no desempenho de HER pode se originar da densidade de carga aumentada de átomos C dopados com P, indicando que os átomos de P são inerentemente vantajosos em interagir com átomos de H do que átomos de C. Também notamos que H * é absorvido em C em vez de P, indicando que o aumento da densidade de carga pode contribuir para o eletrocatalisador no átomo de H. Portanto, nossos cálculos mostram que a dopagem de P no PG pode levar a uma adsorção aprimorada de H * em átomos de C. Como mencionado acima, os cálculos DFT também sugeriram que o doping P em PG poderia aumentar muito mais eficientemente a atividade HER do que o doping S.

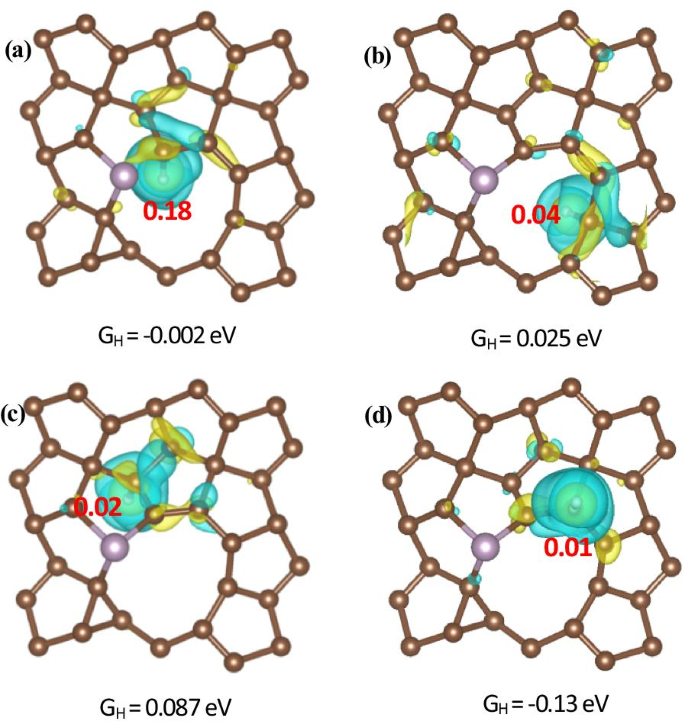
Vistas superiores da diferença de densidade de carga de elétrons e análise de cargas de Bader para um C _2-DOWN vacância e PG dopado com P com H adsorvido no a C1, b C _2-DOWN , c C _{2-DOWN n} e d C _2-UP sites. O nível de isosuperfície é 0,004 e / Bohr ³ . As cores amarela e azul representam o acúmulo e a redução de carga, respectivamente

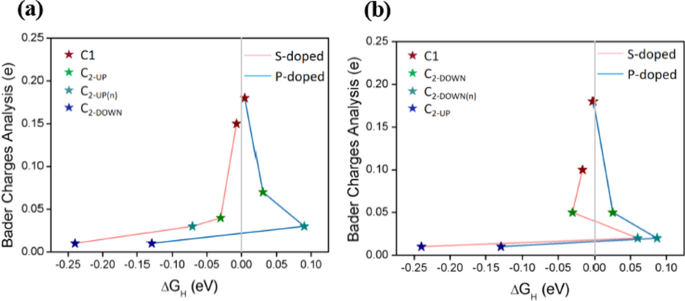
Relação entre Δ G _H e análise de cobranças de Bader para a V _C-UP S-dopado, V _C-UP P-dopado e b V _C-DOWN S-dopado, V _C-DOWN Estruturas dopadas com P. O Δ G _H valores e locais ativos são mostrados na Tabela 3

Atividade de defeito e PG dopado em direção a ELA

Energias Livres de Gibbs DELA

O Δ G _H é o descritor vital do HER para uma variedade de eletrocatalisadores, o Δ G ideal _H valor para um eletrocatalisador é zero, então a adsorção e dessorção de H * podem ocorrer espontaneamente sem barreira de energia de ativação [61, 62]. Para avaliar a atividade HER do PG e investigar a engenharia de defecção e dopagem, calculamos o Δ G _H de ELA. Um de nossos resultados de cálculo sobre Δ G _H versus a coordenada de reação do HER para PG é mostrado na Fig. 8, onde C1 e C2 dentro dos colchetes são locais ativos para a adsorção de hidrogênio.

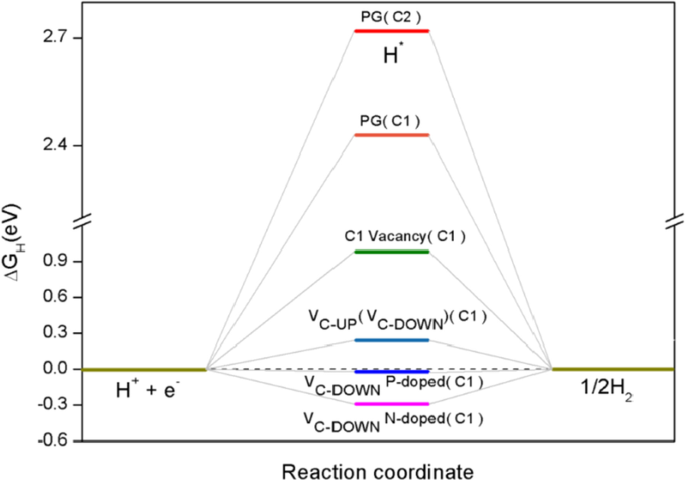
Energia livre de Gibbs versus coordenada de reação do HER para PG, onde C1 e C2 dentro dos colchetes são sítios ativos para adsorção de hidrogênio

Nossos cálculos mostram que o PG puro é considerado inerte para o HER com uma energia livre de Gibbs relativamente grande de H * (Δ G _H =2,72 eV (C2), Δ G _H =2,43 eV (C1)). Quando as vagas são introduzidas, existem dois locais de vaga C diferentes, o local de vaga C1 e o local de vaga C2. Calculamos o Δ G _H nos dois sites e descobriu que a vaga C2 pode diminuir notavelmente Δ G _H (Δ G _H =0,24 eV), o que indica que H * adsorve preferencialmente em estruturas de vacância C2. As estruturas otimizadas com locais de vacância C2 (V _C-UP e V _C-DOWN ) são mostrados na Fig. 2. Embora as vacâncias C2 mostrem uma melhora significativa em relação ao PG puro, elas ainda não são as ideais para a adsorção de hidrogênio, então a engenharia de dopagem é explorada para melhorar o desempenho de HER. Mostramos nossos efeitos das vacâncias C2 e dopagem de heteroátomo S, P na atividade HER e otimizamos o desempenho dela. O Δ G _H os valores estão resumidos na Tabela 3 e os sítios ativos para a evolução do hidrogênio são mostrados na Fig. 3.

Os resultados do cálculo revelam que Δ G _H diminui significativamente, demonstrando que a defecção e a engenharia de dopagem são muito eficazes na redução de Δ G _H . Notavelmente, descobrimos que o Δ G _H valores de sites ativos C1, C _2-UP e C _{2-UP (n)} para V _C-UP , sites ativos C1, C _2-DOWN e C _{2-DOWN (n)} para V _C-DOWN estão muito próximos de zero, especialmente para dois locais C1, significando que as condições ideais podem ser alcançadas, que são significativamente superiores ao PG puro. E comparamos nossos resultados com trabalhos anteriores de outros pesquisadores sobre grafeno, por exemplo, grafeno com vacância C (Δ G _H =- 2,108 eV) [28], grafeno com N-dopado (Δ G _H =- 0,693 eV) [28], grafeno com vacância C e dopado com N (Δ G _H =- 0,595 eV) [28], grafeno com S-dopado (Δ G _H =- 0,30 eV) [29] e grafeno com N / S co-dopado (Δ G _H =- 0,12 eV) [29]. Podemos descobrir que a engenharia de defecção e dopagem são mais eficazes para PG. Assim, nossos resultados sugerem claramente que o Δ G _H de PG pode ser manipulado pela aplicação de engenharia de defecção e dopagem para atingir a atividade HER ideal.

As vias de reação de defeito e PG dopado

O HER prossegue em um processo eletroquímico de várias etapas, por meio de uma das duas vias conhecidas como mecanismos de Volmer – Tafel e Volmer – Heyrovsky. A primeira etapa de HER é a adsorção de H * na superfície do eletrocatalisador (ou seja, reação de Volmer), que é descrita por H ⁺ + E ^- → H *. Então, H * combina com H ⁺ e um elétron (e ^- ) para formar um H ₂ molécula, conhecida como etapa de Heyrovsky, que é descrita por H * + H ⁺ + E ^- → H ₂ . Alternativamente, H ₂ molécula pode ser formada através da etapa Tafel, ou seja, a combinação de dois H * na superfície do eletrocatalisador, que é descrito por 2H * → H ₂ [63].

Para investigar os efeitos da defecção e da engenharia de dopagem no PG e compreender melhor o mecanismo da atividade superior de HER, as barreiras de energia das reações de Tafel e Heyrovsky com C _2-UP e C _2-DOWN vacâncias, PG dopado com S-, P para o sítio C1 foram calculados. O estado inicial (IS), o estado final (FS) e o estado de transição (TS) são exibidos na Fig. 9 com as barreiras de energia correspondentes. Para a reação de Tafel, a recombinação de 2H * mostra barreiras de energia de 1,51 eV (dopado com S), 1,32 eV (dopado com P), respectivamente. Considerando o lançamento de um H ₂ A molécula na reação de Heyrovsky envolvida em um próton reagindo com um H * adsorvido precisa superar as barreiras de energia de 1,01 eV (dopado com S) e 0,99 eV (dopado com P), respectivamente. Os resultados revelam que as barreiras de energia da reação de Tafel são significativamente maiores do que as da reação de Heyrovsky. Portanto, o HER em defeito e PG dopado prefere o mecanismo Volmer-Heyrovsky.

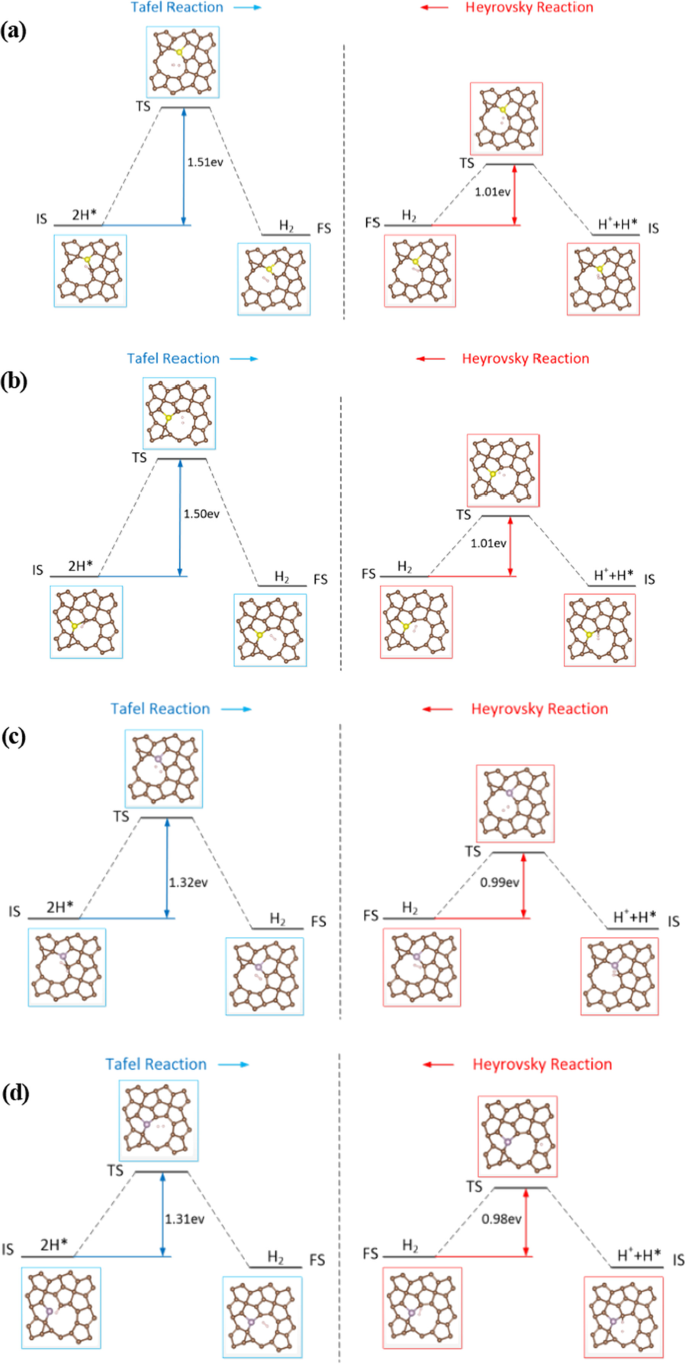
Percursos esquemáticos para o HER. Perfis de energia para as reações de Tafel e Heyrovsky com a C _2-UP vaga e PG dopado com S, b C _2-DOWN vaga e PG dopado com S, c C _2-UP vaga e PG dopado com P, d C _2-DOWN vaga e PG dopado com P. O estado inicial (IS), o estado de transição (TS) e o estado final (FS) são indicados no diagrama com as barreiras de energia correspondentes

Conclusões

Teoricamente, projetamos uma vacância C e PG dopado com N, S e P e investigamos a estabilidade e o papel exclusivo do eletrocatalisador em relação a HER sistematicamente. Descobrimos que a engenharia de deserção e dopagem possui um desempenho de HER superior sobre o PG puro. É importante ressaltar que a atividade de HER ideal pode ser alcançada com vacâncias de C2 e dopagem de heteroátomos S, P, o que indica que as propriedades catalíticas do defeito e do PG dopado podem ser ajustadas de maneira fácil e eficaz. Nossos cálculos revelam que Δ G _H diminui significativamente com as vacâncias C2 e dopagem de heteroátomo S, P, e as condições ideais podem ser alcançadas com dopagem P em sítios ativos C1, para os quais a defecção ou a engenharia de dopagem sozinhas não podem atingir as condições ideais. A análise da estrutura eletrônica mostra que quando a vacância C2 e dopagem com heteroátomo S, P são introduzidos, vários novos estados de deserção se movem para mais perto do nível de Fermi, levando a um gap mais estreito e uma melhora na força de adsorção de hidrogênio. Também encontramos a transferência de carga de PG para H * calculando as diferenças de densidade de carga do elétron, quanto maior a transferência de carga para H *, mais próximo Δ G _H valores a zero usando a análise de cargas de Bader, que indica o desempenho ideal para um catalisador HER. E ainda demonstramos que o HER em defeitos e PG dopado prefere o mecanismo de Volmer-Heyrovsky. Portanto, nosso estudo mostra que o defeito projetado e PG dopado é altamente ativado em direção ao eletrocatalisador HER, a atividade HER ideal pode ser alcançada e locais de atividade catalítica abundantes são fornecidos. Espera-se que as estratégias desenvolvidas neste artigo possam ser aplicadas para projetar eletrocatalisadores 2D à base de grafeno para aplicações HER de baixo custo e alto desempenho.

Disponibilidade de dados e materiais

Os conjuntos de dados que suportam as conclusões deste artigo estão incluídos no artigo, e mais informações sobre os dados e materiais podem ser disponibilizados ao interessado mediante solicitação motivada dirigida ao autor correspondente.

Abreviações

HER:: Reação de evolução de hidrogênio
PG:: Pentagrafeno
2D:: Bidimensional
Δ G _H :: A energia livre de Gibbs
TMDs:: Os dichalcogenetos de metais de transição
VASP:: Pacote de simulação Ab initio de Viena
PAW:: Onda aumentada projetada
PBE:: The Perdew – Burke – Ernzerhof
GGA:: A aproximação do gradiente generalizado
CI-NEB:: O elástico de escalada cutucado por imagem
IS:: Estado inicial
FS:: O estado final
TS:: O estado de transição

Fabricação fácil de BiF3:Ln (Ln =Gd, Yb, Er) @PVP Nanopartículas para imagens de tomografia computadorizada de alta eficiência O papel da apoptose na citotoxicidade induzida por nanopartículas de óxido de zinco frescas e envelhecidas

Nanomateriais

Materiais Poliméricos

biológico

Corante

Especiarias