Efeitos de tamanho e agregação / aglomeração de nanopartículas nas propriedades interfaciais / interfase e resistência à tração de nanocompósitos de polímero

Resumo

Neste estudo, várias equações simples são sugeridas para investigar os efeitos do tamanho e da densidade no número, área de superfície, eficiência de enrijecimento e área de superfície específica de nanopartículas em nanocompósitos poliméricos. Além disso, os papéis do tamanho das nanopartículas e da espessura da interfase nas propriedades da interface / interfase e na resistência à tração dos nanocompósitos são explicados por várias equações. Os agregados / aglomerados de nanopartículas também são assumidos como grandes partículas em nanocompósitos, e suas influências nas características das nanopartículas, propriedades de interface / interfase e resistência à tração são discutidas. O tamanho pequeno afeta vantajosamente o número, a área de superfície, a eficiência de endurecimento e a área de superfície específica das nanopartículas. Apenas 2 g de nanopartículas isoladas e bem dispersas com raio de 10 nm ( R =10 nm) e densidade de 2 g / cm ³ produzir a área interfacial significativa de 250 m ² com matriz de polímero. Além disso, apenas uma interfase espessa não pode produzir parâmetros interfaciais / interfaciais elevados e propriedades mecânicas significativas em nanocompósitos porque o tamanho do enchimento e os agregados / aglomerados também controlam esses termos. Verifica-se que uma interfase espessa ( t =25 nm) em torno das grandes nanopartículas ( R =50 nm) apenas melhora o B parâmetro de interfase para cerca de 4, enquanto B =13 é obtido pelas menores nanopartículas e pela interfase mais espessa.

Histórico

Os nanocompósitos exibem propriedades substanciais por apenas pequeno conteúdo de nanofiller [1,2,3,4,5]. As propriedades importantes dos nanocompósitos poliméricos causam uma ampla gama de aplicações em várias tecnologias, como materiais e bens avançados, medicamentos, dispositivos de energia e sensores [6]. Os estudos de diferentes tipos de nanocompósitos poliméricos visam a obtenção de produtos de alto desempenho por um processo de fácil fabricação e baixo custo.

As propriedades consideráveis ​​dos nanocompósitos poliméricos são atribuídas a boas propriedades interfaciais entre a matriz polimérica e as nanopartículas, como a área interfacial e a interação / adesão na interface [7,8,9,10,11,12,13]. Os altos níveis de propriedades interfaciais levam à formação de outra fase como interfase em torno das nanopartículas, que é diferente tanto da matriz polimérica quanto das nanopartículas, mostra a vantagem dos nanocompósitos em relação aos micro-compósitos convencionais [14,15,16,17,18]. Muitas investigações teóricas sobre propriedades de interface / interfase forneceram uma grande quantidade de informações para atingir as propriedades desejáveis. No entanto, a alta área de superfície das nanopartículas e a forte interação atrativa entre as partículas resultam na agregação / aglomeração [19, 20]. Os conjuntos fortes e densos de nanopartículas denotam a agregação, mas as partículas fracamente articuladas mostram a aglomeração que pode ser quebrada por estresse mecânico [21].

A agregação / aglomeração de nanopartículas reduz o potencial de aumento das propriedades mecânicas em nanocompósitos, devido à restrição da área interfacial [22, 23]. Portanto, o principal desafio na produção de nanocompósitos inclui a obtenção de pequenas nanopartículas e boa dispersão das nanopartículas. É vital superar as forças de atração entre as nanopartículas que produzem a agregação / aglomeração, ao invés de perturbar a estrutura das nanopartículas. Surpreendentemente, Dorigato et al. [24] sugeriram um modelo que mostra que a agregação do filler primário reforça os nanocompósitos poliméricos, enquanto as nanopartículas aglomeradas comumente induzem efeitos negativos no desempenho mecânico dos nanocompósitos poliméricos [21, 25]. Nesse sentido, o estudo da agregação / aglomeração de nanopartículas é necessário para revelar seus reais efeitos nas propriedades dos nanocompósitos. Embora o tamanho das nanopartículas seja assumido como um benefício atraente em nanocompósitos poliméricos, os efeitos do isolamento ou agregação / aglomeração nas principais propriedades das nanopartículas, como número, área superficial e área superficial específica, não foram estudados na literatura. Além disso, a agregação / aglomeração de nanopartículas tem sido assumida como um termo geral que altera qualitativamente o comportamento dos nanocompósitos. Além disso, os possíveis papéis das dimensões das nanopartículas e da interfase nas propriedades da interface / interfase não foram descritos em estudos anteriores.

Métodos

Neste artigo, os efeitos do tamanho e da densidade do enchimento no número, área de superfície, eficiência de enrijecimento e área de superfície específica de nanopartículas em nanocompósitos poliméricos são explicados por equações apropriadas. Além disso, a agregação / aglomeração de nanopartículas é assumida como partículas grandes e suas influências em vários termos são reveladas. Da mesma forma, os possíveis papéis de nanopartículas e tamanhos de interfase nos parâmetros de interface / interfase e resistência à tração de nanocompósitos são discutidos. O foco principal deste artigo são as nanopartículas esféricas, mas outras geometrias das nanopartículas podem ser estudadas pelo desenvolvimento das equações sugeridas.

O número de nanopartículas isoladas esfericamente em um nanocompósito pode ser calculado pelo peso das nanopartículas ( W _f ) Como:
$$ N =\ frac {W_f} {d_f \ frac {4} {3} \ pi {R} ^ 3}. $$ (1)
onde d _f e R são a densidade e o raio das nanopartículas, respectivamente. Nesta condição, a área de superfície total de nanopartículas dispersas é dada por:
$$ A =N \ left (4 \ pi {R} ^ 2 \ right). $$ (2)
A pode ser considerada como a área interfacial entre a matriz polimérica e as nanopartículas. Substituição de N da Eq. 1 na Eq. 2 leva a:
$$ A =\ frac {3 {W} _f} {d_fR}. $$ (3)
que se correlaciona com o A com W _f , d _f , e R .

Cada nanopartícula introduz um efeito de enrijecimento na matriz polimérica por envolvimento mecânico das cadeias poliméricas. O nível de compartilhamento de tensões entre a matriz polimérica e as nanopartículas depende da área interfacial e da rigidez das nanopartículas. Como resultado, um novo parâmetro como a eficiência de enrijecimento das nanopartículas pode ser definido como:
$$ SE ={AE} _f =\ frac {3 {W} _f} {d_fR} {E} _f. $$ (4)
onde E _f é o módulo de nanopartículas de Young. A eficiência de enrijecimento em função das propriedades das nanopartículas expressa a capacidade das nanopartículas para o enrijecimento de nanocompósitos. Além disso, a área de superfície específica das partículas é expressa como:
$$ {A} _c =\ frac {A} {m} =\ frac {A} {d_fv} =\ frac {4 \ pi {R} ^ 2} {d_f \ frac {4} {3} \ pi { R} ^ 3} =\ frac {3} {d_fR}. $$ (5)
onde m e v são a massa total e o volume das nanopartículas, respectivamente. Este parâmetro expressa a área superficial de 1 g de partículas e, portanto, não depende da concentração de nanopartículas no nanocompósito.

Agora, a resistência à tração e as propriedades interfaciais / interfaciais são fornecidas por equações simples. Pukanszky [26] sugeriu um modelo para resistência à tração de compósitos em função do conteúdo de enchimento e propriedades interfaciais / interfase como:
$$ \ sigma ={\ sigma} _m \ frac {1 - {\ varphi} _f} {1 + 2,5 {\ varphi} _f} \ exp \ left (B {\ varphi} _f \ right). $$ (6)
onde σ _m mostra a resistência à tração da matriz de polímero e φ _f é a fração de volume do nanocarregador. Este modelo foi originalmente sugerido para compósitos, mas mostrou boa concordância com os resultados experimentais de diferentes nanocompósitos poliméricos. Uma boa concordância é obtida entre os dados experimentais de resistência à tração e as previsões da equação de Pukanszky em muitas amostras como PP / SiO ₂ [27], PEEK / SiO ₂ [28], PVC / CaCO ₃ [29], PP / CaCO ₃ [30], e PVC / SiO ₂ [31] calculando o B parâmetro como 4,12, 3,15, 3,07, 2,5 e 2,1, respectivamente. Esses exemplos validam a aplicação do modelo de Pukanszky para a resistência à tração de nanocompósitos poliméricos.

B é um parâmetro interfacial que mostra o nível de adesão interfacial por:
$$ B =\ left (1+ {A} _c {d} _ft \ right) \ ln \ left (\ frac {\ sigma_i} {\ sigma_m} \ right). $$ (7)
onde t e σ _i são a espessura e a resistência da interfase, respectivamente.

Substituição de A _c da Eq. 5 na última equação apresenta:
$$ B =\ left (1 + 3 \ frac {t} {R} \ right) \ ln \ left (\ frac {\ sigma_i} {\ sigma_m} \ right). $$ (8)
Aplicar a equação acima no modelo de Pukanszky oferece a força relativa ( σ / σ _m ) Como:
$$ {\ sigma} _R =\ frac {1 - {\ varphi} _f} {1 + 2,5 {\ varphi} _f} \ exp \ left [\ left (1 + 3 \ frac {t} {R} \ right ) \ ln \ left (\ frac {\ sigma_i} {\ sigma_m} \ right) {\ varphi} _f \ right]. $$ (9)
que liga explicitamente a resistência à tração às propriedades de enchimento e interfase. Além disso, devemos indicar os efeitos do tamanho, que sem dúvida existem na modelagem da fratura [32,33,34].

A fração de volume da interfase ( φ _i ) para nanocompósitos contendo nanopartículas esféricas pode ser considerado [35] por:
$$ {\ varphi} _i =\ left [{\ left (\ frac {R + t} {R} \ right)} ^ 3-1 \ right] {\ varphi} _f. $$ (10)
em que t =0 resultados em φ _i =0 indicando a ausência de interfase no nanocompósito. Os modelos analíticos neste estudo podem ser aplicáveis ​​onde outros modelos, como zona coesa, descrevem as regiões interfásicas. Alguns estudos anteriores consideraram a interfase por alguns modelos, como o elemento finito 2D [36, 37].

Em nosso trabalho anterior [38], a parâmetro de interfase para nanocompósitos de polímero reforçados com nanopartículas esféricas foi definido como:
$$ a =10 \ left (\ frac {t} {R} \ right) \ left (\ frac {10 {E} _i} {E_f} -1 \ right). $$ (11)
onde E _i é o módulo de interfase. Esta equação correlaciona o a a vários parâmetros eficazes de nanocondicionamento e interfase. a foi calculado para alguns nanocompósitos variando de 0,8 a 19 [38]. Foi relatado que um nível mais alto de a introduz um módulo melhor em nanocompósitos.

Resultados e discussão

Na primeira parte desta seção, os efeitos do tamanho e da densidade nas diferentes propriedades das nanopartículas são traçados por gráficos de contorno e os resultados são discutidos para esclarecer a influência da agregação / aglomeração. Na próxima etapa, os papéis do raio das nanopartículas (incluindo a agregação / aglomeração) e a espessura da interfase nas propriedades interfaciais / interfase e o desempenho dos nanocompósitos são estudados.

A Figura 1 ilustra a agregação / aglomeração de nanopartículas em um nanocompósito. Quando as nanopartículas isoladas e dispersas são acumuladas, pode-se presumir que uma grande nanopartícula é formada. De acordo com a Fig. 1, se nanopartículas isoladas com R agregado / aglomerado de raio, uma grande partícula é produzida com alto raio. Como resultado, a agregação / aglomeração de nanopartículas pode ser fisicamente assumida pelo crescimento do tamanho de partícula em nanocompósitos. Essa ocorrência afeta as características das nanopartículas e da interfase que finalmente mudam o comportamento dos nanocompósitos.

Ilustração esquemática da agregação / aglomeração de nanopartículas em nanocompósitos poliméricos. Quando várias nanopartículas com raio R são agregados / aglomerados, uma grande partícula é formada

A Figura 2 mostra as funções de R e d _f em ln (N) e A níveis constantes W _f =2 g. De acordo com a Fig. 2a, baixo N é observado pelos altos valores de R e d _f , mas N aumenta quando R e d _f diminuir. Assim, a densidade e o tamanho das nanopartículas afetam inversamente o número de partículas nos nanocompósitos de polímero em uma concentração de carga constante. As pequenas nanopartículas com baixa densidade produzem um grande número de nanopartículas em nanocompósitos, enquanto as nanopartículas grandes e densas produzem poucas partículas. Consequentemente, os agregados / aglomerados diminuem significativamente o número de nanopartículas em nanocompósitos a uma concentração de enchimento constante.

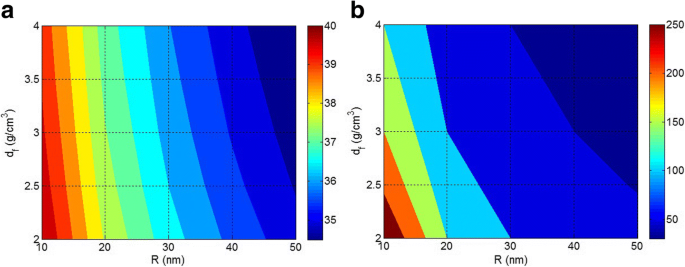
Plotagens de contorno para mostrar as funções de R e d _f parâmetros em a ln ( N ) e b A (m ² ) em W _f =2 g

A Figura 2b ilustra os efeitos de R e d _f parâmetros na área de superfície total das nanopartículas ( A em m ² ) em W _f =2 g. A área de superfície das nanopartículas é assumida como a área interfacial entre o polímero e as nanopartículas, transferindo a tensão da matriz para as nanopartículas. O estresse pode ser transportado de forma eficiente do polímero para as nanopartículas para melhorar as propriedades mecânicas, quando a área interfacial é grande o suficiente [39, 40]. Conforme observado na Fig. 2b, a maior área interfacial é alcançada pelos menores intervalos de R e d _f . Também é interessante que apenas 2 g de nanopartículas isoladas e bem dispersas com R =10 nm e d _f =2 g / cm ³ produzir cerca de 250 m ² área interfacial com matriz polimérica. No entanto, a área interfacial reduz com o aumento do tamanho e densidade das nanopartículas e A abaixo de 50 m ² é obtido em R > 40 nm e d _f > 3 g / cm ³ . A diferença significativa entre as áreas interfaciais em diferentes tamanhos de partícula indica que o tamanho das nanopartículas é um parâmetro importante em nanocompósitos. As grandes nanopartículas causam pequena área interfacial que deteriora a vantagem significativa das nanopartículas em nanocompósitos. Deve-se notar que a concentração de preenchimento em nanocompósitos pode não ser muito alta em comparação com micro-compósitos, mas a extraordinária área de superfície das nanopartículas comumente resulta na interação entre partículas e agregação / aglomeração. Como resultado, embora os altos teores de nanopartículas em nanocompósitos fortaleçam o acúmulo, a agregação / aglomeração de nanopartículas geralmente ocorre em nanocompósitos de polímero em diferentes concentrações de preenchimento que diminuem a área interfacial e enfraquecem o desempenho.

A Figura 3a exibe os gráficos de contorno de ln (SE) como uma função de R e d _f em W _f =2 ge E _f =100 GPa. A eficiência de enrijecimento das nanopartículas aumenta quando pequenas nanopartículas com baixa densidade são incorporadas na matriz polimérica, demonstrando que o tamanho das nanopartículas exerce um papel efetivo no enrijecimento das nanopartículas em nanocompósitos poliméricos. Por outro lado, as nanopartículas agregadas / aglomeradas deterioram o desempenho dos nanocompósitos poliméricos pela redução da eficiência das nanopartículas. As pequenas nanopartículas com baixa densidade aumentam significativamente a rigidez dos nanocompósitos por meio do grande nível de transferência de tensões entre as cadeias poliméricas e as nanopartículas. Um estudo anterior nesta área explicou a física da influência do raio de carga na transferência de tensões da matriz polimérica para a fibra usando as simulações de dinâmica molecular [41]. No entanto, as partículas grandes e densas não podem introduzir a alta rigidez das nanopartículas na matriz do polímero, sugerindo um compósito com pouca rigidez. Portanto, as características das nanopartículas controlam significativamente as propriedades dos nanocompósitos.

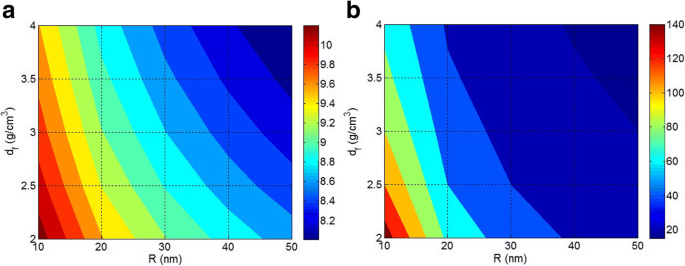
Os efeitos de R e d _f em a ln (SE) com ln (m ² Unidade GPa) e b A _c (m ² / g) em W _f =2 ge E _f =100 GPa

A Figura 3b também mostra os níveis de A _c parâmetro em R diferente e d _f valores em W _f =2 ge E _f =100 GPa. Observa-se que o melhor A _c é obtido por nanopartículas pequenas e de baixa densidade, enquanto o pior é produzido por partículas grandes e densas. O A _c valor de cerca de 140 m ² / g é obtido por R =10 nm e d _f =2 g / cm ³ , enquanto A _c nível de menos de 20 m ² / g é mostrado pelo grande tamanho de partícula e alta densidade. Como resultado, R e d _f parâmetros mostram efeitos negativos em A _c em nanocompósitos poliméricos. Conclui-se que A _c parâmetro que expressa a área interfacial de nanopartículas isoladas de 1 g dá os melhores níveis por pequenas nanopartículas. Como resultado, as grandes nanopartículas ou agregados / aglomerados não podem produzir um considerável A _c o que diminui a eficiência das nanopartículas em nanocompósitos poliméricos. Sabe-se que o desempenho dos nanocompósitos, como propriedades mecânicas, de retardamento de chama e de barreira, está diretamente relacionado à área interfacial entre o polímero e as nanopartículas [10, 42]. Um grande A _c pode produzir níveis aceitáveis ​​para as propriedades dos nanocompósitos por uma pequena quantidade de nanopartículas, devido à alta área interfacial entre a matriz polimérica e as nanopartículas. Assim, controlar o tamanho e a densidade das nanopartículas é um desafio em nanocompósitos para criar as melhores propriedades.

Agora, os efeitos dos tamanhos das nanopartículas e da interfase nas propriedades interfaciais / interfase e resistência à tração dos nanocompósitos são explicados pelas equações propostas. A Figura 4 ilustra os efeitos de R e t em B parâmetro interfacial e resistência à tração pelo modelo de Pukanszky (Eq. 6) em σ _i / σ _m =5 e φ _f =0,02. Com base na Fig. 4a, o B nível de 13 é obtido pelas menores nanopartículas e a interfase mais espessa. Além disso, B diminui para menos de 3 quando o tamanho das nanopartículas cresce para cerca de 40 nm e a espessura da interfase diminui para menos de 10 nm. Portanto, os tamanhos das nanopartículas e da interfase desempenham papéis diferentes em B parâmetro. Além disso, deve-se notar que as pequenas nanopartículas sem a formação de uma interfase forte não podem dar um alto B em nanocompósitos poliméricos. Por outro lado, uma interface espessa ( t =25 nm) em torno das grandes nanopartículas ( R =50 nm) apenas melhora o B parâmetro para cerca de 4. Como resultado, as dimensões da nanopartícula e da interfase são importantes para obter um alto nível de B em nanocompósitos. No entanto, a um nível constante de espessura de interfase, o crescimento do tamanho das nanopartículas por agregação / aglomeração diminui B parâmetro que demonstra os efeitos negativos de agregados / aglomerados nas propriedades interfaciais / interfase.

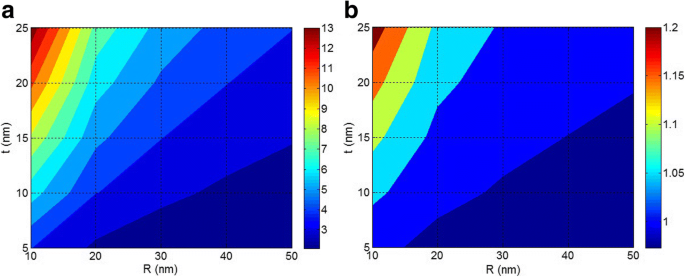
a B parâmetro interfacial e b resistência à tração relativa pelo modelo de Pukanszky em diferentes faixas de R e d _f e constante σ _i / σ _m =5 e ϕ _f =0,02

A Figura 4b também mostra os efeitos de R e t parâmetros de resistência à tração de nanocompósitos pelo modelo de Pukanszky. Observa-se que nanopartículas pequenas e interfase espessa melhoram a resistência dos nanocompósitos. No entanto, uma fraca resistência é observada por partículas grandes e interfase fina. Portanto, ambos R e t parâmetros afetam a resistência à tração dos nanocompósitos. Além disso, verifica-se que a resistência dos nanocompósitos diminui à medida que o tamanho das nanopartículas aumenta, devido à agregação / aglomeração. Assim, é essencial isolar e dispersar as nanopartículas em matriz polimérica em tamanho pequeno para obter os melhores desempenhos. Uma vez que as nanopartículas tendem naturalmente à agregação / aglomeração, a modificação de sua superfície ou funcionalização das cadeias poliméricas pode prevenir o acúmulo [19, 43, 44].

A Figura 5 mostra as dependências da fração de volume da interfase ( φ _i ) e a parâmetro de interfase em R e t parâmetros em φ _f =0,02, E _f =100 GPa e E _i =50 GPa. De acordo com a Fig. 5a, as menores nanopartículas e a interfase mais espessa fornecem o nível mais alto de φ _i como 0,8, que reforça significativamente o nanocompósito. Este nível de φ _i é mais do que φ _f demonstrando as funções eficazes de R e t parâmetros no desempenho de nanocompósitos. Além disso, φ _i diminui para cerca de 0 em R > 30 nm, ou seja, uma interfase espessa ( t =25 nm) não pode fazer um alto φ _i em nanocompósitos poliméricos, quando grandes nanopartículas são incorporadas à matriz polimérica. Esta ocorrência mostra o papel significativo do tamanho das nanopartículas na formação das regiões de interfase. Assim, o tamanho das nanopartículas muda consideravelmente as propriedades da interfase revelando que a agregação / aglomeração das nanopartículas diminui principalmente a concentração da interfase, o que causa módulo e resistência pobres nos nanocompósitos [5, 45]. Deve ser mencionado que as regiões de interfase podem se sobrepor nos sistemas contendo alta concentração de enchimento. Portanto, a equação expressa para φ _i (Eq. 10) é razoável para nanocompósitos normais contendo baixo teor de preenchimento.

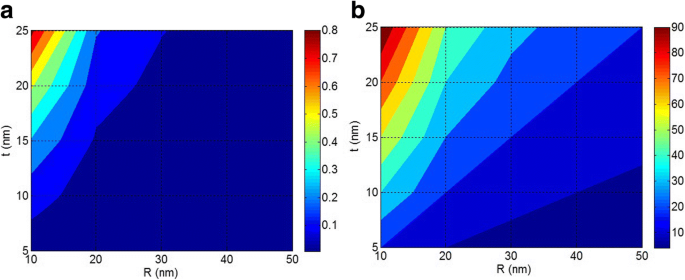
A correlação de a ϕ _i e b a parâmetro de interfase para R e t parâmetros em ϕ _f =0,02, E _f =100 GPa e E _i =50 GPa

A Figura 5b também mostra os efeitos de R e t níveis em a parâmetro interfase. a aumenta por pequenas nanopartículas e interfase espessa, enquanto dá menos valores (menos de 10) em R > 40 nm e t <10 nm. Esta evidência revela que a depende de ambos R e t parâmetros. Desde um alto a parâmetro melhora o módulo de Young dos nanocompósitos [38], pequenas nanopartículas e interfase espessa são desejáveis ​​para o desempenho dos nanocompósitos. De acordo com a Fig. 5b, os agregados / aglomerados de nanopartículas (alto R ) produz um leve a evento por interfase espessa. Esta ocorrência indica que uma forte interfase não pode dar um ótimo a ou alto módulo quando as nanopartículas são agregadas / aglomeradas em nanocompósitos. Como resultado, os agregados / aglomerados de nanopartículas causam efeitos negativos nas propriedades dos nanocompósitos poliméricos. Com base nas observações mencionadas, a agregação / aglomeração enfraquece os benefícios das nanopartículas e propriedades de interface / interfase; portanto, as nanopartículas não podem apresentar um forte reforço em nanocompósitos poliméricos.

Conclusões

Os efeitos do tamanho e da densidade do enchimento, bem como da espessura da interfase nas características das nanopartículas e das propriedades da interface / interfase, foram estudados por meio de equações simples. Além disso, os agregados / aglomerados de nanopartículas foram assumidos como partículas grandes e suas influências nos parâmetros de interfase e na resistência à tração dos nanocompósitos foram discutidas. O tamanho pequeno e a baixa densidade causam níveis significativos de número, área de superfície, eficiência de endurecimento e área de superfície específica das nanopartículas. Apenas 2 g de nanopartículas pequenas e bem dispersas ( R =10 nm) com d _f =2 g / cm ³ pode produzir cerca de 250 m ² área interfacial com matriz polimérica. Por outro lado, o tamanho grande e os agregados / aglomerados enfraquecem os atributos positivos das nanopartículas em nanocompósitos. Nanopartículas pequenas e interfase espessa apresentam os altos níveis de B parâmetro, resistência à tração, fração de volume de interfase e a parâmetro interfase. B diminui para menos de 3 quando o tamanho das nanopartículas cresce para cerca de 40 nm e a espessura da interfase reduz para menos de 10 nm. No entanto, B =13 é obtido pelas menores nanopartículas ( R =10 nm) e a interfase mais espessa ( t =25 nm). Esta ocorrência confirma que as propriedades interfaciais / interfaciais dependem do tamanho das nanopartículas além da interação / adesão interfacial. Além disso, as nanopartículas grandes produzem propriedades interfaciais / interfaciais baixas e baixa resistência à tração, mesmo em altas espessuras de interfase, revelando o papel principal do tamanho das partículas. As menores nanopartículas e a interfase mais espessa fornecem o nível mais alto de φ _i , enquanto φ _i diminui para cerca de 0 em R > 30 nm. Esta evidência demonstra que apenas uma interface espessa ( t =25 nm) não pode fazer um alto φ _i quando grandes nanopartículas ou agregados / aglomerados estão presentes em nanocompósitos. Consequentemente, as nanopartículas agregadas / aglomeradas afetam negativamente as propriedades interfaciais / interfase e resistência à tração de nanocompósitos de polímero.

O Surfactante Aniônico / Líquidos Iônicos Óxido de Grafeno Reduzido Intercalado para Supercapacitores de Alto Desempenho Um estudo da variabilidade na memória de acesso aleatório resistiva de contato por modelo de vacância estocástica