Uma metodologia de duas etapas para estudar a influência da agregação / aglomeração de nanopartículas no módulo de Young de nanocompósitos poliméricos
Resumo
Uma técnica de duas etapas baseada em modelos micromecânicos é sugerida para determinar a influência de nanopartículas agregadas / aglomeradas no módulo de Young de nanocompósitos poliméricos. Supõe-se que o nanocompósito inclui agregação / aglomeração de nanopartículas e fases de matriz eficazes. Este método é examinado para diferentes amostras, e os efeitos de parâmetros importantes no módulo são investigados. Além disso, os níveis mais alto e mais baixo do módulo previsto são calculados com base na metodologia atual. A técnica sugerida pode prever corretamente o módulo de Young para as amostras, assumindo a agregação / aglomeração de nanopartículas. Além disso, a agregação / aglomeração de nanopartículas diminui o módulo de Young dos nanocompósitos de polímero. É demonstrado que o alto módulo das nanopartículas não é suficiente para obter um alto módulo nos nanocompósitos, e a química da superfície dos componentes deve ser ajustada para evitar agregação / aglomeração e para dispersar nanopartículas na matriz polimérica.
Histórico
Muitos pesquisadores têm se concentrado em nanocompósitos de polímero nos últimos anos, a fim de determinar os parâmetros eficazes nas relações de propriedades de estrutura de processamento e para otimizar o desempenho geral medido por propriedades mecânicas, térmicas, físicas e de barreira [1,2,3,4 ] Um baixo conteúdo de nanopartículas em nanocompósitos poliméricos produz grande área interfacial, alto módulo, baixo peso e produtos baratos que são extremamente atraentes na indústria de compósitos. Nesse sentido, a aplicação de nanopartículas é uma maneira fácil, eficiente e econômica de melhorar o desempenho de matrizes poliméricas. Os efeitos de muitos materiais e parâmetros de processamento nas propriedades de nanocompósitos de polímero contendo camadas de silicato (nanoargila), nanotubos de carbono (CNT) e cargas inorgânicas, como sílica (SiO 2 ) e carbonato de cálcio (CaCO 3 ) foram investigados [5,6,7,8].
O tamanho e a qualidade da dispersão / distribuição das nanopartículas na matriz polimérica alteram as propriedades gerais dos nanocompósitos poliméricos. As nanopartículas tendem a se agregar e aglomerar, devido à atração entre as nanopartículas como as forças de van der Waals e ligações químicas [9] ou a forte redução na separação da superfície conforme o tamanho do enchimento diminui [10]. Portanto, é difícil dispersar as nanopartículas em matrizes poliméricas em nanoescala. Tanto a agregação quanto a aglomeração são montagens de nanopartículas, onde a agregação inclui colônias fortes e densas de partículas, mas a aglomeração compreende partículas fracamente combinadas que podem ser rompidas por forças mecânicas. Aglomeração / agregação é evidente em altos conteúdos de preenchimento, o que deteriora a nanoescala de preenchimento e produz muitos defeitos e concentrações de tensão em nanocompósitos [11,12,13]. A aglomeração / agregação também reduz a área interfacial entre a matriz polimérica e as nanopartículas, o que diminui o envolvimento mecânico das cadeias poliméricas nas nanopartículas e elimina o efeito de enrijecimento. Nossos achados recentes [14, 15] e o estudo de Ji et al. [16] sobre propriedades mecânicas indicaram que qualquer agregação / aglomeração prejudica severamente o efeito de enrijecimento das nanopartículas em nanocompósitos poliméricos.
Além da caracterização experimental dos nanocompósitos, as investigações teóricas que quantificam a dependência do comportamento mecânico das propriedades das fases constituintes e da morfologia geométrica das nanopartículas têm apresentado desafios atrativos em pesquisas recentes. Estudos teóricos podem ajudar a elucidar os resultados experimentais e facilitar a síntese ideal de nanocompósitos altamente promissores. As nanopartículas em nanocompósitos introduzem desordem na matriz adjacente, levando à formação de zonas de interfase ao redor do enchimento, que apresentam propriedades diferentes da matriz bulk e nanopartículas [17,18,19]. Estudos teóricos sobre as propriedades da interfase têm mostrado resultados atrativos, justificando o uso de nanopartículas em nanocompósitos poliméricos [20,21,22].
Os efeitos da agregação / aglomeração no desempenho mecânico de nanocompósitos foram investigados em trabalhos anteriores [11, 14, 23, 24]. Esses estudos geralmente consideram a agregação / aglomeração por grandes partículas. Recentemente, métodos de modelagem multiescala têm sido usados para estudar as propriedades dos nanocompósitos [25,26,27]. No presente trabalho, um método de duas etapas é sugerido para examinar o papel da agregação / aglomeração de nanopartículas no módulo de Young de nanocompósitos de polímero, assumindo a fração de fase de agregação / aglomeração em nanocompósitos e a porção de nanopartículas em agregados / aglomerados. A este respeito, dois modelos micromecânicos de Paul e Maxwell são aplicados para expressar o módulo de Young dos nanocompósitos. Numerosos dados experimentais são apresentados para avaliar as previsões. Além disso, os efeitos dos parâmetros de agregação / aglomeração no módulo de Young dos nanocompósitos são estudados.
Métodos
Quando uma fração de nanopartículas agrega / aglomerados, uma distribuição não uniforme de nanopartículas é mostrada no nanocompósito. Como resultado, algumas nanopartículas podem ser assumidas em regiões esféricas na matriz como fase de agregação / aglomeração e outras estão uniformemente dispersas na matriz de polímero, conforme ilustrado na Fig. 1. Consequentemente, a nanopartícula mostra duas partes com reforço diferente que pode ser considerou duas fases diferentes no cálculo como fases de agregação / aglomeração e matriz efetiva que demonstram as regiões dentro e fora das esferas, respectivamente (Figura 1).
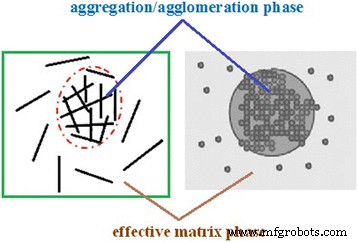
Ilustração esquemática de agregação / aglomeração e fases de matriz eficazes em nanocompósitos de polímero contendo nanopartículas esféricas e em camadas
Os dois parâmetros a seguir são sugeridos para o nível de agregação / aglomeração de nanopartículas em nanocompósito de polímero:
$$ z =\ frac {V _ {\ mathrm {agg}}} {V} $$ (1) $$ y =\ frac {V_f ^ {\ mathrm {agg}}} {V_f} $$ (2)
onde “ V agg ”E“ V ”Denotam os volumes totais da fase de agregação / aglomeração e nanocompósito, respectivamente. Além disso, “ V f agg ”E“ V f ”Mostram os volumes de nanopartículas na fase de agregação / aglomeração e nanocompósito inteiro, respectivamente. A fração de volume de nanopartículas incorporadas na fase de agregação / aglomeração é apresentada por:
$$ {\ phi} _f ^ {\ mathrm {agg}} =\ frac {V_f ^ {\ mathrm {agg}}} {V _ {\ mathrm {agg}}} =\ frac {y {\ phi} _f} {z} $$ (3)
onde “ ϕ f ”É a fração de volume de nanocompósitos em nanocompósitos. Além disso, a fração de volume de nanopartículas bem dispersas incorporadas na fase de matriz efetiva (fora da fase de agregação / aglomeração) é calculada por:
$$ {\ phi} _f ^ {\ mathrm {mat}} =\ frac {V_f- {V} _f ^ {\ mathrm {agg}}} {V- {V} _ {\ mathrm {agg}}} =\ frac {\ left (1-y \ right) {\ phi} _f} {1-z} $$ (4)
Neste estudo, uma metodologia de duas etapas baseada nos modelos micromecânicos é usada para determinar os parâmetros de agregação / aglomeração ( z e y ) em nanocompósitos de polímero pelo módulo de Young. Em primeiro lugar, o módulo de agregação / aglomeração e as fases efetivas da matriz são calculados pelo modelo de Paul. Em segundo lugar, a fase de agregação / aglomeração é assumida como inclusões esféricas na matriz efetiva e o módulo de Young do nanocompósito é calculado pelo modelo de Maxwell para um compósito contendo partículas dispersas.
Paul [28] sugeriu um modelo que assume a tensão macroscopicamente homogênea em dois componentes do composto como:
$$ E ={E} _ {\ mathrm {m}} \ frac {1+ \ left (a-1 \ right) {\ phi} _f ^ {2/3}} {1+ \ left (a-1 \ right) \ left ({\ phi} _f ^ {2/3} - {\ phi} _f \ right)} $$ (5) $$ a =\ frac {E _ {\ mathrm {f}}} {E_ {\ mathrm {m}}} $$ (6)
onde “ E m ”E“ E f ”São módulos de Young da matriz de polímero e fases de enchimento, respectivamente. Na primeira etapa, o módulo de agregação / aglomeração ( E agg ) e matriz efetiva ( E tapete ) fases são calculadas pelo modelo de Paul através da substituição de “ ϕ f ”Com“ \ ({\ phi} _f ^ {agg} \) ”e“ \ ({\ phi} _f ^ {mat} \) ”como:
$$ {E} _ {\ mathrm {agg}} ={E} _ {\ mathrm {m}} \ frac {1+ \ left (a-1 \ right) {\ phi_f ^ {\ mathrm {agg}} } ^ {2/3}} {1+ \ left (a-1 \ right) \ left ({\ phi_f ^ {\ mathrm {agg}}} ^ {2/3} - {\ phi} _f ^ {\ mathrm {agg}} \ right)} ={E} _ {\ mathrm {m}} \ frac {1+ \ left (a-1 \ right) {\ left (\ frac {y {\ phi} _f} { z} \ right)} ^ {2/3}} {1+ \ left (a-1 \ right) \ left [{\ left (\ frac {y {\ phi} _f} {z} \ right)} ^ {2/3} - \ frac {y {\ phi} _f} {z} \ right]} $$ (7) $$ {E} _ {\ mathrm {m} \ mathrm {at}} ={E} _ {\ mathrm {m}} \ frac {1+ \ left (a-1 \ right) {\ phi_f ^ {\ mathrm {m} \ mathrm {at}}} ^ {2/3}} {1+ \ esquerda (a-1 \ direita) \ esquerda ({\ phi_f ^ {\ mathrm {m} \ mathrm {at}}} ^ {2/3} - {\ phi} _f ^ {\ mathrm {m} \ mathrm { at}} \ right)} ={E} _ {\ mathrm {m}} \ frac {1+ \ left (a-1 \ right) {\ left [\ frac {\ left (1-y \ right) { \ phi} _f} {1-z} \ right]} ^ {2/3}} {1+ \ left (a-1 \ right) \ left [{\ left (\ frac {\ left (1-y \ direita) {\ phi} _f} {1-z} \ right)} ^ {2/3} - {\ left (\ frac {\ left (1-y \ right) {\ phi} _f} {1-z } \ right)} ^ {2/3} \ right]} $$ (8)
Além disso, o modelo de Maxwell [29] para compósitos contendo cargas dispersas é dado por:
$$ E ={E} _ {\ mathrm {m}} \ frac {1 + 2 {\ phi} _f \ left (a-1 \ right) / \ left (a + 2 \ right)} {1- { \ phi} _f \ left (a-1 \ right) / \ left (a + 2 \ right)} $$ (9)
Na segunda etapa, o modelo de Maxwell é aplicado para o cálculo do módulo em um compósito contendo uma matriz efetiva (matriz e nanopartículas bem dispersas) e fases de agregação / aglomeração pela substituição de “ ϕ f ”Com“ z ”(Ver Eq. 1),“ E f ”Com o módulo de fase de agregação / aglomeração ( E agg ) e “ E m ”Com o módulo de matriz efetiva ( E tapete ) Como:
$$ E ={E} _ {\ mathrm {mat}} \ frac {1 + 2z \ left (k-1 \ right) / \ left (k + 2 \ right)} {1-z \ left (k- 1 \ direita) / \ esquerda (k + 2 \ direita)} $$ (10) $$ k ={E} _ {\ mathrm {agg}} / {E} _ {\ mathrm {mat}} $$ ( 11)
que correlaciona o módulo de Young de nanocompósitos aos módulos de agregados / aglomerados e a matriz efetiva, bem como o parâmetro "z". Quando “ E agg ”E“ E tapete ”Das Eqs. 7 e 8 são inseridos nas últimas equações, o módulo dos nanocompósitos é expresso usando a concentração de preenchimento, módulo de preenchimento, módulo de matriz e “ z ”E“ y ”Parâmetros. A dependência do módulo sobre esses parâmetros é razoável, porque as propriedades do polímero e das nanopartículas, bem como a extensão da agregação / aglomeração do material de enchimento, controlam o módulo dos nanocompósitos. Na presente metodologia, y > z é significativo, porque \ ({VV} _f ^ {\ mathrm {agg}}> {V} _f {V} _ {\ mathrm {agg}} \).
Resultados e discussão
O método proposto é aplicado para avaliar a agregação / aglomeração de nanopartículas em várias amostras de estudos anteriores, incluindo PVC / CaCO 3 [30], PCL / nanoargila [31], ABS / nanoargila [32], PLA / nanoargila [33], PET / MWCNT [34] e poliimida / MWCNT [35]. A Figura 2 mostra os resultados experimentais do módulo de Young, bem como as previsões do método de duas etapas. Os cálculos seguem adequadamente os dados experimentais em diferentes concentrações de nanocargas, ilustrando a exatidão do método sugerido. No entanto, a maior concordância entre os dados experimentais e teóricos é obtida quando a agregação / aglomeração de nanopartículas são assumidas por níveis adequados de “ z ”E“ y ”Parâmetros. As maiores previsões de “ z ”E“ y ”Parâmetros são calculados como z =0,2 e y =0,95 para PVC / CaCO 3 nanocompósito. Além disso, ( z , y ) são obtidos valores de (0,3, 0,75), (0,1, 0,99) e (0,35, 0,7) para amostras de PCL / nanoargila, PLA / nanoargila e PET / MWCNT, respectivamente. Além disso, ( z , y ) os níveis de (0,2, 0,93) e (0,15, 0,9) são calculados para nanocompósitos PET / MWCNT e poliimida / MWCNT, respectivamente. Esses níveis de “ z ”E“ y ”Parâmetros demonstram a formação de nanopartículas agregadas / aglomeradas nos nanocompósitos mencionados. A pequena melhoria do módulo nessas amostras confirma a fraca dispersão e o alto nível de acúmulo de nanopartículas nas matrizes poliméricas. Por exemplo, a adição de 7,5% em peso de CaCO 3 para PVC apenas aumenta o módulo de PVC puro (1,13 GPa) para 1,3 GPa. Além disso, a incorporação de 10% em peso de nanoargila em PCL apenas melhora o módulo de PCL puro de 0,22 para 0,37 GPa. No entanto, as nanopartículas apresentam um módulo elevado em comparação com as matrizes poliméricas. Módulo de Young de CaCO 3 , nanoargila e MWCNT foram relatados como 26, 180 e 1000 GPa [36], respectivamente, enquanto o módulo de Young das matrizes poliméricas presentes dificilmente atinge 2,5 GPa. Como resultado, as nanopartículas agregadas / aglomeradas diminuem significativamente o módulo em nanocompósitos, e a presente metodologia sugere dados aceitáveis para agregação / aglomeração de nanopartículas em nanocompósitos poliméricos.
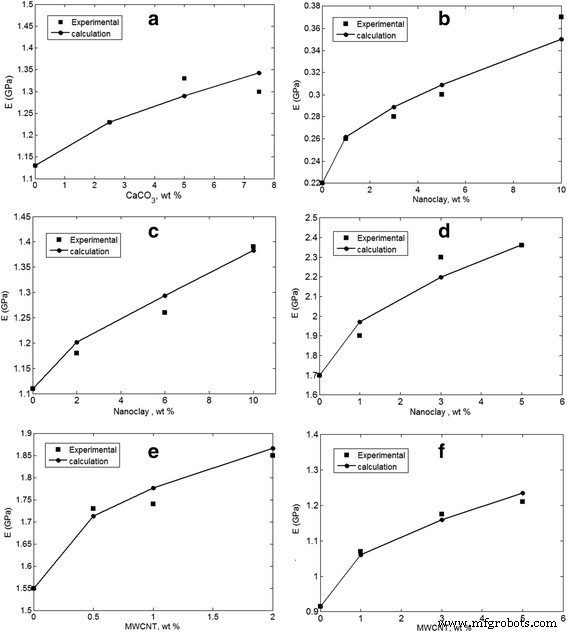
A diferença entre os resultados experimentais e teóricos assumindo a agregação / aglomeração de nanopartículas para a PVC / CaCO 3 [30], b PCL / nanoargila [31], c ABS / nanoargila [32], d PLA / nanoargila [33], e PET / MWCNT [34] e f amostras de poliimida / MWCNT [35]
Os módulos maiores e menores previstos pela metodologia atual são calculados e ilustrados na Fig. 3 em uma média E m =2 GPa e E f =200 GPa. O módulo máximo é obtido pelos menores valores de “ z ”E“ y ”Parâmetros; por exemplo, z =0,00001 e y =0,00001 (eles não podem ser 0). Por outro lado, o “ y ”Nível de 0,99 resulta na agregação / aglomeração de todas as nanopartículas, o que reduz significativamente o módulo. Além disso, o nível mais alto de “ z ”(Extensão máxima de aglomeração) causa o módulo mínimo. “ z ”Como a fração de volume de enchimento aglomerado no nanocompósito é menor do que a fração de volume de todas as nanopartículas ( ϕ f ) Então, z = ϕ f pode sugerir o menor nível de módulo. A diferença significativa entre os valores superior e inferior do módulo mostra o importante papel da agregação / aglomeração das nanopartículas na rigidez dos nanocompósitos. A agregação / aglomeração de nanopartículas nos nanocompósitos diminui muito o módulo de Young em diferentes concentrações de preenchimento, enquanto uma fina dispersão de nanopartículas sem agregação / aglomeração produz um bom módulo. Além disso, a alta agregação / aglomeração em grandes teores de nanocargas diminui a taxa de crescimento do módulo ao aumentar em “ ϕ f ”. Portanto, é importante ajustar os parâmetros de material e processamento para evitar a agregação / aglomeração de nanopartículas que promovem a concentração de tensões e defeitos ou descolamento em nanocompósitos poliméricos [37, 38].
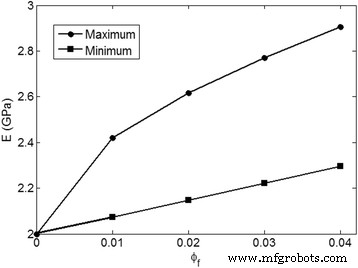
Os níveis máximo e mínimo de módulo previstos pela presente metodologia na média E m =2 GPa e E f =200 GPa
A Figura 4 ilustra os efeitos de “ z ”E“ y ”Parâmetros no módulo em E m =3 GPa, E f =150 GPa e ϕ f =0,02. O módulo mais alto é obtido nos menores níveis de “ z ”E“ y ”Parâmetros, confirmando o papel positivo da boa dispersão / distribuição das nanopartículas no módulo dos nanocompósitos. No entanto, o módulo diminui muito como “ y ”Parâmetro aumenta. De acordo com a Eq. 2, “ y ”Mostra a concentração de nanopartículas na fase de aglomeração / agregação. Um módulo baixo é observado em alto “ y ”, Que mostra que uma grande fração de nanopartículas na fase de aglomeração / agregação enfraquece um nanocompósito. Consequentemente, nanopartículas aglomeradas / agregadas causam um efeito negativo no módulo dos nanocompósitos. Portanto, muito esforço deve ser feito para facilitar a dispersão / distribuição das nanopartículas na matriz polimérica, que depende da interação / adesão interfacial entre o polímero e as nanopartículas e dos parâmetros de processamento. Estudos anteriores relataram resultados valiosos nesta área e sugeriram várias técnicas para melhorar esta dispersão [39,40,41].
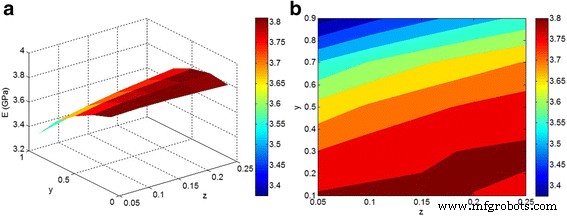
a , b Os cálculos do módulo pelas Eqs. 10-11 em função de “ z ”E“ y ”Em E m =3 GPa, E f =150 GPa e ϕ f =0,02
A Figura 5 demonstra a dependência do módulo previsto em “ E m ”E“ E f ”Parâmetros na média ϕ f =0,02, z =0.3 e y =0,5 com a técnica atual. Observa-se que o módulo depende de ambos “ E m ”E“ E f ”Fatores em baixo E f <150 GPa. No entanto, um módulo mais alto de nanopartículas não altera o módulo do nanocompósito. Como resultado, o módulo dos nanocompósitos depende apenas de “ E m ”Quando“ E f ”É superior a 150 GPa. Isso sugere que a alta rigidez das nanopartículas não desempenha um papel principal no módulo do nanocompósito, e muita atenção deve ser dada à dispersão / agregação / aglomeração das nanopartículas.
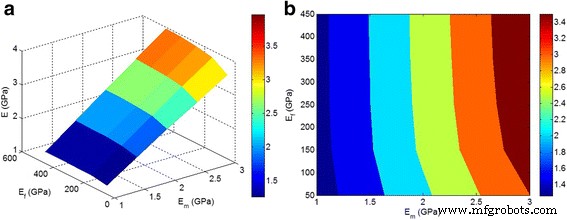
a , b Os efeitos de “ E m ”E“ E f ”No módulo previsto pelas Eqs. 10-11 em média ϕ f =0,02, z =0.3 e y =0,5
Conclusões
Uma técnica de duas etapas foi sugerida para determinar as influências das nanopartículas agregadas / aglomeradas no módulo de Young dos nanocompósitos poliméricos. Os modelos de Paul e Maxwell foram aplicados para calcular os módulos de agregação / aglomeração e as fases efetivas da matriz. As previsões da metodologia sugerida mostraram boa concordância com os dados experimentais de diferentes amostras, assumindo parâmetros de agregação / aglomeração corretos. Consequentemente, a presente metodologia pode dar resultados aceitáveis para agregação / aglomeração de nanopartículas em nanocompósitos poliméricos. A agregação / aglomeração de nanopartículas diminuiu significativamente o módulo de Young, enquanto uma dispersão fina de nanopartículas produziu um módulo alto. O módulo mais alto foi obtido no menor “ z ”E“ y ”Parâmetros, que confirmaram o papel positivo da boa dispersão / distribuição das nanopartículas no módulo dos nanocompósitos. No entanto, o módulo diminui conforme o “ y ”Parâmetro aumentado. Além disso, verificou-se que as excelentes características das nanopartículas, como alto módulo, não são suficientes para atingir as propriedades ideais em nanocompósitos poliméricos. Consequentemente, muita atenção deve ser focada na dispersão / distribuição de nanopartículas na matriz polimérica dependendo da interação / adesão interfacial entre o polímero e as nanopartículas e os parâmetros de processamento.
Nanomateriais
- A função do aninhamento na impressão 3D de polímero
- A detecção fotoeletroquímica aprimorada de ácido úrico em nanopartículas de Au Eletrodo de carbono vítreo modificado
- Nanofibras de polímero por eletrofiação decoradas com nanopartículas de metal nobre para detecção química
- O estudo de um novo sistema micelar em forma de verme aprimorado por nanopartículas
- Estudo de primeiros princípios sobre a estabilidade e imagem STM de Borophene
- Estudo in vitro da influência das nanopartículas de Au nas linhas celulares HT29 e SPEV
- Propriedades de formação e luminescência de Al2O3:Nanocompósitos de SiOC na base de nanopartículas de alumina modificados por feniltrimetoxisilano
- Influência da Água na Estrutura e Propriedades Dielétricas da Microcristalina e Nano-Celulose
- Método de pós-tratamento para a síntese de nanopartículas FePt-Fe3O4 binárias monodispersas
- Estudo Numérico de um Absorvedor Solar Eficiente Composto por Nanopartículas de Metal



