Projeto de pontos quânticos GeSn / GeSiSn com engenharia de tensão para emissão de bandgap direta de infravermelho médio no substrato de Si

Resumo

Pontos quânticos GeSn / GeSiSn auto-montados projetados por engenharia de deformação na matriz Ge foram numericamente investigados com o objetivo de estudar sua potencialidade para a emissão direta de bandgap na faixa de infravermelho médio. O uso da liga GeSiSn como meio circundante para pontos quânticos GeSn (QD) permite ajustar a deformação ao redor do QD através da variação da composição de Si e / ou Sn. Consequentemente, a incompatibilidade de rede entre os pontos quânticos GeSn e a camada circundante GeSiSn foi ajustada entre - 2,3 e - 4,5% através da variação da composição da barreira Sn para diferentes tamanhos de QD em forma de cúpula. Os resultados obtidos mostram que o comprimento de onda de emissão, atendendo aos critérios de diretividade QD específicos, pode ser sucessivamente sintonizado em uma ampla faixa de infravermelho médio de 3 a 7 μm, abrindo novas perspectivas para fontes de laser do grupo IV totalmente integradas em sistemas fotônicos de Si para aplicações de detecção.

Histórico

Recentemente, a demonstração de materiais do grupo IV de bandgap direto através da liga de Ge [1, 2] e SiGe [3, 4] com o estanho tem motivado intensas atividades de pesquisa devido às oportunidades reais e praticamente implementáveis para fotônica e eficiência eletrônica on-chip integração. De fato, foi demonstrado que a liga GeSn exibe bandgap direto além de certa composição por meio da diminuição mais rápida de Γ em comparação com o vale L [5,6,7,8]. Embora os resultados relatados sejam muito encorajadores, as propriedades do material e as potencialidades de aplicação ainda não foram totalmente exploradas. De fato, o principal caminho realmente disponível para aumentar o comprimento de onda operacional de lasers semicondutores baseados em GeSn, em direção à janela de transparência da atmosfera que se sobrepõe às linhas de absorção de vários gases [9], inclui o aumento do conteúdo de Sn nas camadas de GeSn [10, 11 ] No entanto, devido à grande incompatibilidade de rede entre Ge e Sn (14%), a preservação da qualidade cristalográfica do material aparece como o principal desafio que impede este objetivo [12, 13]. Uma solução potencialmente interessante para aumentar o comprimento de onda de emissão e garantir melhores confinamentos de portadores em estruturas dimensionais mais baixas, como nanofios [14,15,16], nanobastões [17] e pontos quânticos [18]. Dentro dos critérios específicos de franqueza, o comprimento de onda de emissão entre bandas de gap direto é teoricamente limitado a 4,3 μm [19]. Para superar essas limitações, é necessário introduzir um grau adicional de liberdade na concepção de estruturas quânticas baseadas no grupo IV. Isso pode ser garantido usando a camada GeSiSn ternária [20,21,22], como um material circundante para pontos quânticos GeSn (QD), oferecendo a possibilidade de engenharia de deformação incorporando composições de Si e Sn adequadas . Consequentemente, o uso da camada de engenharia de deformação GeSiSn em torno de GeSn QD deve oferecer uma gama maior de comprimento de onda de emissão de gap direto acessível.

Neste contexto, relatamos um estudo teórico do efeito da engenharia de deformações, variando a composição de Sn na camada GeSiSn em torno do GeSn QD no comprimento de onda de emissão inter-bandas direto do bandgap.

Métodos

Uma vez que os deslocamentos de banda entre ligas do grupo IV contendo Sn binários e ternários e Ge não são experimentalmente conhecidos, o alinhamento de banda relativo entre os diferentes semicondutores do grupo IV envolvidos neste trabalho é avaliado, com respeito à borda da banda de valência de Ge, usando a teoria simplificada de Jaros de deslocamentos de banda [23] conforme detalhado por D'Costa et al. [24]. Os efeitos de deformação decorrentes da incompatibilidade de rede entre o substrato Ge e a camada GeSiSn e entre o GeSn QD e o material GeSiSn circundante foram avaliados para as bordas da banda de condução e valência.

De fato, a borda da banda de condução é deslocada por \ (\ delta {E} _c ^ i \) e a da banda de valência por δE _v conforme mostrado na Eq. (1) e (2):
$$ \ delta {E} _c ^ i ={a} _c ^ i \ left ({\ varepsilon} _ {xx} + {\ varepsilon} _ {yy} + {\ varejpsilon} _ {zz} \ right) $ $ (1) $$ \ delta {E} _v ={a} _v \ left ({\ varepsilon} _ {xx} + {\ varepsilon} _ {yy} + {\ varepsilon} _ {zz} \ right) + b \ left ({\ varepsilon} _ {xx} - {\ varepsilon} _ {zz} \ right) $$ (2)
onde eu denota vale L ou Γ, a _c e a _v são o potencial de deformação da banda de condução e valência, respectivamente, e b é o potencial de deformação por cisalhamento. \ ({\ varepsilon} _ {xx} ={\ varepsilon} _ {yy} =\ varepsilon =\ left (\ frac {a_s- {a} _ {\ mathrm {l}}} {a _ {\ mathrm {l }}} \ right) \) é a cepa no plano e \ ({\ varepsilon} _ {zz} =- 2 \ frac {C_ {12}} {C_ {11}} {\ varepsilon} _ {xx} \) é a tensão na direção do crescimento. a _s e a _l são, respectivamente, o parâmetro de rede do substrato e a camada tensionada. C ₁₁ e C ₁₂ são as constantes de rigidez.

Os parâmetros binários e ternários do material da liga são derivados dos de Ge, Si e Sn por interpolação linear. Esses parâmetros são retirados da Referência [11].

Os espaçamentos deformados dependentes da composição podem ser avaliados adicionando os deslocamentos de energia gerados por deformação correspondentes ao espaçamento de tensões do material não tensionado dado na Eq. (3) para GeSn e Eq. (4) para GeSiSn:
$$ {E} _g ^ i \ left ({\ mathrm {Ge}} _ {1- {X} _d} {\ mathrm {Sn}} _ {X_d} \ right) =\ left (1- {X} _d \ right) {E} _g ^ i \ left (\ mathrm {Ge} \ right) + {X} _d {E} _g ^ i \ left (\ mathrm {Sn} \ right) - {b} ^ i { X} _d \ left (1- {X} _d \ right) $$ (3) $$ {\ displaystyle \ begin {array} {l} {E} _g ^ i \ left ({\ mathrm {Ge}} _ {1- {x} _b-y} {\ mathrm {Si}} _ y {\ mathrm {Sn}} _ {x_b} \ right) =\ left (1- {x} _b-y \ right) {E} _g ^ i \ left (\ mathrm {Ge} \ right) + {x} _b {E} _g ^ i \ left (\ mathrm {Sn} \ right) + {yE} _g ^ i \ left (\ mathrm {Si } \ right) - {b} _ {\ mathrm {Ge} \ mathrm {Sn}} ^ i {x} _b \ Big (1- {x} _b - \\ {} y \ Big) - {b} _ {\ mathrm {Si} \ mathrm {Sn}} ^ iy \ left (1- {x} _b-y \ right) - {b} _ {\ mathrm {Ge} \ mathrm {Si}} ^ i {x} _by \ end {array}} $$ (4)
onde b é o parâmetro de curvatura de bandgap correspondente das ligas binárias resumidas na Tabela 1.

Para determinar os estados confinados das portadoras e deduzir as energias de transição entre bandas, a equação de Schrödinger de massa efetiva de banda única foi resolvida em coordenadas cartesianas pelo método de elementos finitos fornecido pelo software COMSOL Multiphysics [25]:
$$ - \ frac {{\ mathrm {\ hslash}} ^ 2} {2} \ nabla \ left (\ frac {1} {m ^ {\ ast} \ left (\ overrightarrow {r} \ right)} \ mathrm {\ nabla \ uppsi} \ left (\ overrightarrow {r} \ right) \ right) + V \ left (\ overrightarrow {r} \ right) \ uppsi \ left (\ overrightarrow {r} \ right) =E \ uppsi \ left (\ overrightarrow {r} \ right) $$ (5)
E representa a energia da portadora e ψ é a função de onda correspondente. m * é a massa efetiva do portador, ћ é a constante de Planck reduzida, \ (\ overrightarrow {r} \) é o vetor de coordenadas tridimensionais, e V é o potencial de confinamento do portador (descontinuidade da banda). Para simplificar o procedimento de cálculo da estrutura eletrônica QD, adotamos a aproximação de deformação constante [26, 27] ao invés da abordagem de simulação atômica computacionalmente cara que obviamente poderia dar mais precisão no perfil de distribuição de deformação [28, 29]. De fato, consideramos que o potencial de confinamento de portadores no QD deformado compressivamente é suficientemente profundo para minimizar o impacto da não uniformidade de deformação nos estados confinados de elétrons [27]. Além disso, as bordas da banda de condução, que são os parâmetros mais importantes neste trabalho, permitindo estudar a exatidão do bandgap, são deslocadas apenas pela deformação hidrostática sendo menos sensível à não uniformidade da deformação, especialmente quando uma incompatibilidade de rede relativamente baixa é considerada [30].

Resultados e discussão

Uma vez que estamos principalmente preocupados com o impacto da deformação em torno do GeSn QD, a composição Sn do QD é fixada em 28% e a composição Si do GeSiSn em 35%; o estudo é, portanto, focado no impacto da composição da barreira Sn ( x _b ) variação entre 6 e 22%. A deformação em plano resultante na camada GeSiSn ou no GeSn QD é dada na Fig. 1a.

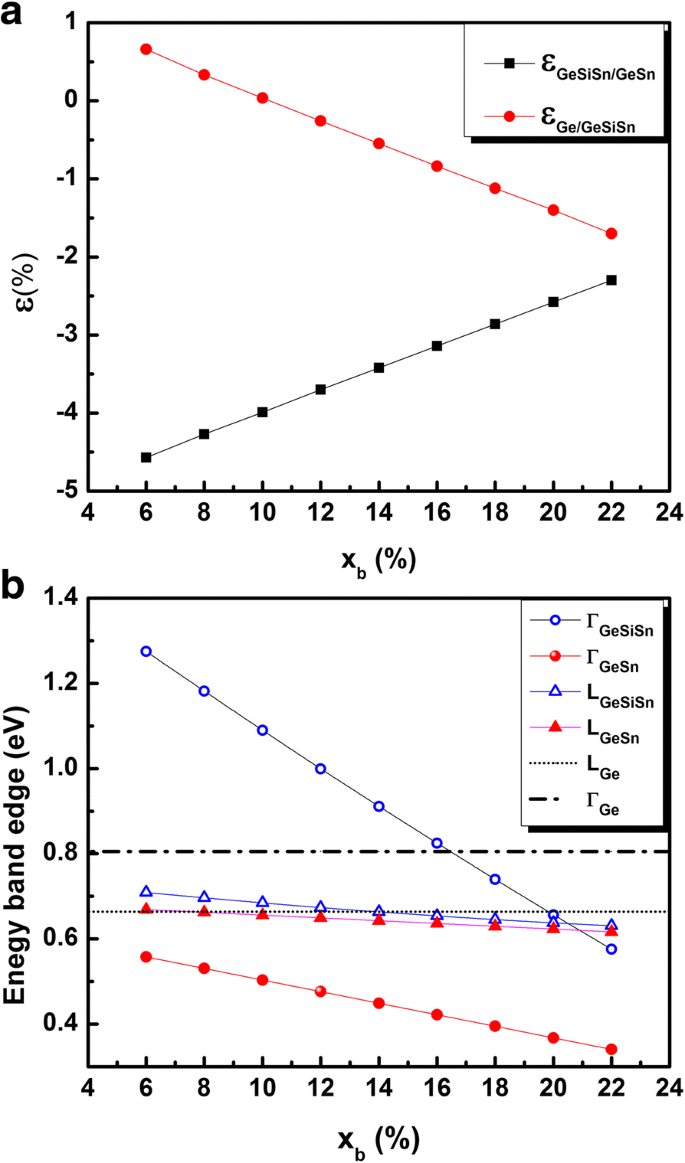
a Lattice mismatch entre Ge _{0,65- xb} Si _0,35 Sn _xb e Ge (círculos preenchidos) e entre Ge _0,72 Sn _0,28 e Ge _{0,65- xb} Si _0,35 Sn _xb (quadrados preenchidos) como uma função de x _{b .} b Bordas da banda nos vales L e G para Ge _{0,65- xb} Si _0,35 Sn _xb , Ge _0,72 Sn _0,28 , e Ge como uma função de x _b

A deformação em plano na camada bidimensional do material GeSiSn varia entre 0,6% ( x _b =6%) e - 1,7% ( x _b =22%). Supomos que esta camada permanece pseudomeorficamente tensionada, permitindo manter a estrutura projetada experimentalmente realizável. O GeSn é escolhido para ser deformado por compressão dentro do material circundante do GeSiSn com uma incompatibilidade de rede variando de - 2,3 a - 4,5%, garantindo condições favoráveis para a formação de GeSn QD auto-organizado.

A Figura 1b mostra a dependência do intervalo tenso nos pontos L e Γ de Ge _0,72 Sn _0,28 e Ge _{(0,65- xb )} Si _0,35 Sn _xb como uma função de x _b . O Γ vale de Ge _0,72 Sn _0,28 o material permanece abaixo dos vales L, atestando seu tipo I para toda a faixa investigada de composição de barreira ao estanho. Enquanto isso, quando o confinamento de elétrons é levado em consideração, o bandgap efetivo aumenta e o efeito do tamanho QD torna-se decisivo [18], especialmente para QD altamente tenso. De fato, na presença de confinamento quântico, a energia do estado fundamental deve ser considerada em vez do mínimo da banda Γ. Consequentemente, é esperado que QD de tamanho menor tenha níveis de energia confinada mais altos no vale Γ que podem exceder o vale L (e / ou nível de energia de elétron do estado fundamental no vale L). Portanto, é importante investigar a faixa de tamanho do QD obedecendo aos critérios de franqueza específicos.

A estrutura modelada é esquematicamente apresentada na Fig. 2. O Ge _0,72 Sn _0,28 QD é considerado como tendo uma forma de cúpula com uma base circular de diâmetro D variando de 15 a 40 nm e altura fixa para razão de diâmetro igual a 0,25. O QD está posicionado dentro da camada GeSiSn de 15 nm de espessura com uma composição de Si de 35% e uma composição de Sn ajustável. Esta estrutura deve ser formada em substrato com buffer de Ge e coberta com camada de Ge.

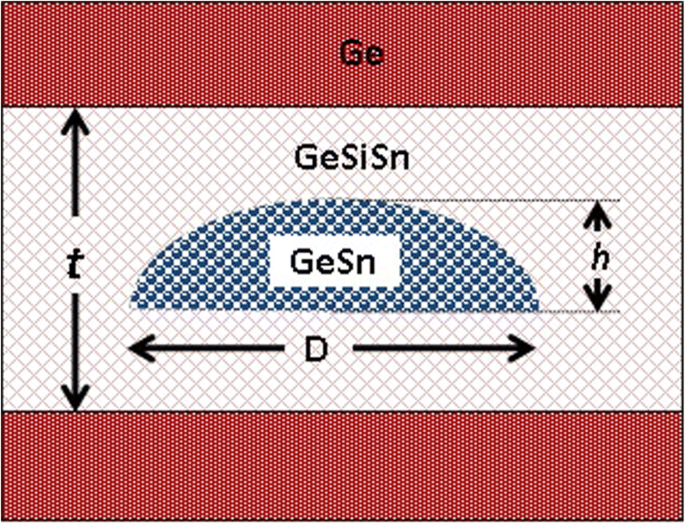
Apresentação esquemática do modelo GeSn QD de altura ( h ) e diâmetro ( D ) dentro da camada de redução de deformação GeSiSn na matriz Ge

Para garantir um projeto QD consistente para uma melhor operação do dispositivo emissor de luz, um parâmetro de objetividade adequado levando em consideração o espaçamento de energia entre a posição de nível de energia confinado de QD mais baixo nos vales L e G foi introduzido [18]. Este parâmetro é denotado por GS _L -GS _Γ e deve ser maior do que a energia térmica da temperatura ambiente para evitar a perda de portadores por ativação térmica, onde GS _L (GS _Γ ) representa o nível de energia do estado fundamental do elétron no vale L (vale Γ) em relação ao máximo da banda de valência. A avaliação do GS _L -GS _Γ é ilustrado esquematicamente na inserção da Fig. 3.

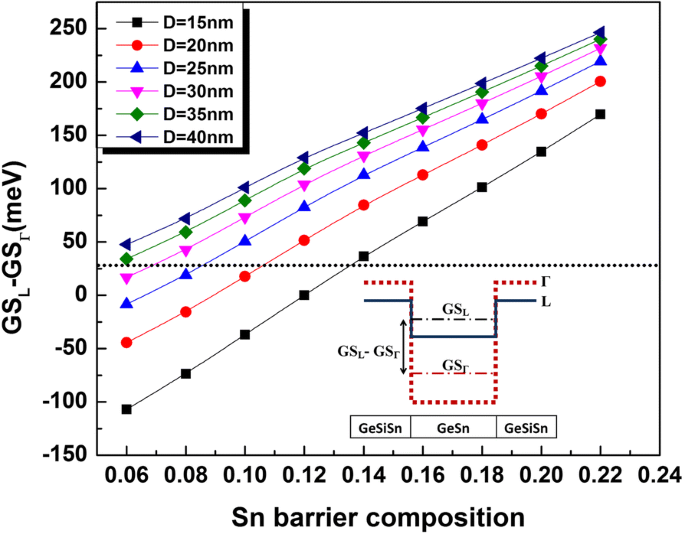
Parâmetro de objetividade (GS _L -GS _Γ ) variação em função do Ge _0,72 Sn _0,28 Tamanho QD e composição Sn do Ge _{0,65- x} Si _0,35 Sn _x camada circundante. A linha pontilhada indica a energia térmica em temperatura ambiente. A inserção representa uma definição esquemática do parâmetro de franqueza

O cálculo dos níveis de energia do elétron GeSn QD em vales Γ e L para diferentes diâmetros em função da composição de Sn em GeSiSn permite obter o parâmetro de objetividade correspondente (GS _L -GS _Γ ) Os resultados são plotados na Fig. 3. Para um dado x _b , o valor de GS _L -GS _Γ é governado principalmente pelo tamanho do QD. Consequentemente, os pontos menores com estados de energia confinada obviamente mais altos requerem energia de bandgap mais baixa por meio da redução de deformação para cumprir os critérios de objetividade. Conforme mostrado pela Fig. 3, pontos maiores ( D > 25 nm) satisfazem GS _L -GS _Γ> 26 meV para x _b superior a 8%. No entanto, o bandgap direto eficiente de QD de tamanho pequeno é garantido para valores mais altos de x _b ( x _b ≥ 14% para D =15 nm).

Dentro dos parâmetros adotados neste trabalho, e especialmente os parâmetros de curvatura dos materiais binários, o aumento do teor de Sn do material GeSiSn reduz a mancha em torno do QD e reduz também o espaçamento entre bandas do material circundante. Na verdade, como mostrado na Fig. 1b, o aumento de x _b de 6 a 22% reduz a descontinuidade da banda de condução no vale Γ de 0,72 eV para 0,23 eV. De fato, como mostrado na Fig. 4, onde a função de onda quadrada \ ({\ left | \ uppsi \ left (\ overrightarrow {r} \ right) \ right |} ^ 2 \) do elétron do estado fundamental em pontos quânticos de o diâmetro de 35 nm é mostrado no plano xy para a composição da barreira de Sn de 6% e 22%, os elétrons estão totalmente localizados dentro do QD, independentemente da composição da barreira (descontinuidade da banda de condução). Os elétrons fortemente confinados indicam maior confiabilidade do QD investigado como um meio ativo para emissores de luz em substrato de Si.

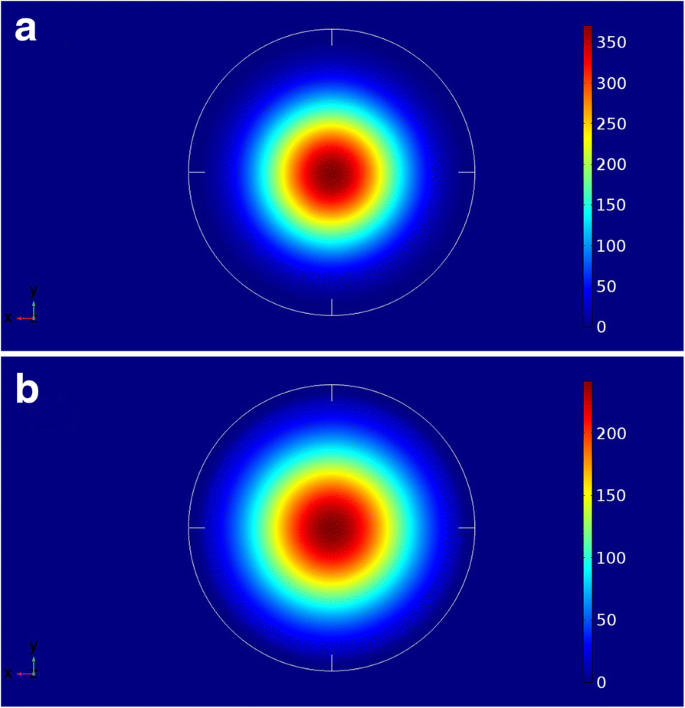
Função de onda do estado fundamental do elétron ao quadrado para Ge _0,72 de 35 nm de diâmetro Sn _0,28 QD para a Xb =6% e b Xb =22%

Limitando os tamanhos de QD para um determinado x _b para aqueles que geram emissão de gap direto eficiente, avaliamos o comprimento de onda de emissão entre bandas do estado fundamental QD. Os resultados são mostrados na Fig. 5, onde o comprimento de onda de emissão é plotado contra x _b para diferentes tamanhos de QD. É importante notar que o maior tamanho de QD considerado neste trabalho ( D =40 nm) mostrou uma pequena separação de energia entre o estado fundamental do elétron e o primeiro estado excitado (abaixo de 26 meV) e, portanto, foi ignorado neste estudo. No entanto, o comprimento de onda de emissão avaliado em função de x _b foi mantido na Fig. 5 com uma linha pontilhada.

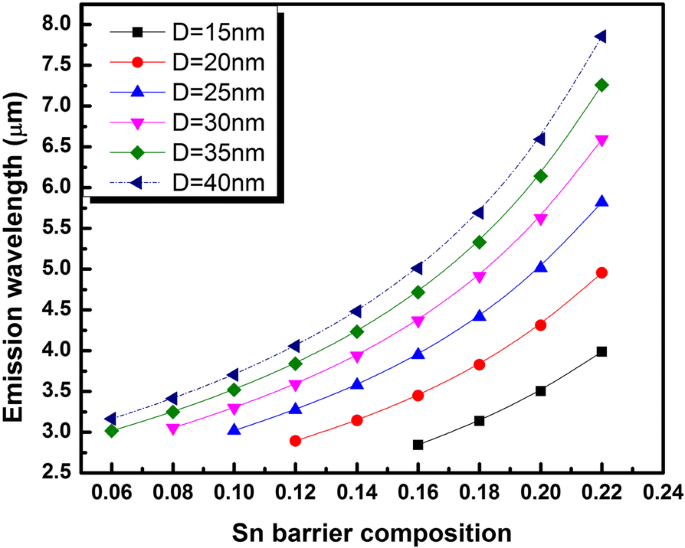
Comprimento de onda de emissão do estado fundamental à temperatura ambiente do intervalo de banda direto Ge _0,72 Sn _0,28 QD em função do tamanho e composição Sn do Ge _{0,65- xb} Si _0,35 Sn _xb camada circundante

A faixa de comprimento de onda projetada para ser coberta pelo projeto QD proposto varia de 3 a 7 μm. A faixa produzida é extremamente importante para a aplicação de detecção de gás. A implementação experimental dessa estrutura pode oferecer a oportunidade de cobrir, pela primeira vez, toda a faixa de infravermelho médio com um material totalmente compatível com a tecnologia microeletrônica existente, abrindo caminho para novas perspectivas em optoeletrônicos de infravermelho médio baseados em QD compatível com CMOS.

Conclusões

GeSn QD na camada de engenharia de deformação GeSiSn na matriz Ge foi investigada como uma função do tamanho de QD e da incompatibilidade da rede com o material circundante. A redução da tensão em torno do QD de GeSn variando a composição Sn do material de barreira GeSiSn é encontrada para aumentar o comprimento de onda de emissão de bandgap direto tipo I de 3 a 7 μm. A estrutura projetada abre novas perspectivas em emissor de luz infravermelho médio totalmente compatível com a tecnologia Si.

Abreviações

CMOS:: Semicondutor de óxido metálico complementar
GS _L :: Nível de elétron do estado fundamental no vale L
GS _Γ :: Nível de elétron do estado fundamental no vale Γ
QD:: Pontos quânticos

Síntese one-pot de nanopartículas de núcleo-shell monodispersas CoFe2O4 @ Ag e sua caracterização Pontos quânticos InP / ZnS dopados com Mn dual-emissivo e ajustável por cor por meio de um método de dopagem de crescimento

Nanomateriais

Materiais Poliméricos

biológico

Corante

Especiarias