A Bifurcação de Suscetibilidade Magnética no Isolador Topológico Sb2Te3 Ni-Dopado com Ordem Antiferromagnética Acompanhada por Alinhamento Ferromagnético Fraco

Resumo

A susceptibilidade magnética revela uma descontinuidade na temperatura de Néel e um loop de histerese com baixo campo coercivo foi observado abaixo da temperatura de Néel. A suscetibilidade magnética dos processos de resfriamento de campo zero e resfriamento de campo coincide em uma temperatura acima da descontinuidade, e eles se dividem na temperatura que impulsiona a descontinuidade. A divisão da susceptibilidade magnética é maior em campos magnéticos externos mais baixos. Não foi observada mais divisão de susceptibilidade magnética em um campo magnético acima de 7000 Oe, o que é consistente com a energia da anisotropia magnética. Nosso estudo confirma que essas características de suscetibilidade magnética se originam de uma ordem antiferromagnética acompanhada de ferromagnetismo fraco.

Introdução

Os isoladores topológicos tridimensionais possuem um estado de superfície sem intervalos de dispersão linear que é protegido pela simetria de reversão do tempo [1, 2]. O estado da superfície topológica consiste em férmions de Dirac filtrados por spin. Esta textura helicoidal de spin do estado da superfície topológica tem atraído muita atenção devido às suas possíveis aplicações elétricas e relacionadas ao spin [3,4,5,6,7,8,9,10,11,12,13,14 , 15,16,17,18,19,20]. Além das características exóticas intrínsecas, a introdução da magnetização no isolador topológico modificará o eletrônico. Essa interação de troca entre o elétron de condução e os átomos magnéticos quebra a simetria da reversão do tempo e isso abre uma lacuna no estado da superfície de Dirac. O férmion de Dirac no estado de superfície torna-se massivo [1, 2, 21] e leva a muitas propriedades interessantes, como o efeito Hall anômalo quântico, [22, 23] efeito magnetoelétrico topológico [24], sintonia do modo de borda quiral [ 25, 26] e trança Majorana [27,28,29]. O portador do estado da superfície topológica domina essas propriedades magnetoelétricas. Muitos trabalhos experimentais foram realizados em filmes finos dopados com Mn, Cr e V (Bi, Sb) \ (_ {2} \) Te \ (_ {3} \) para realizar a previsão teórica [30]. A maioria desses estudos focou principalmente nas propriedades de transporte elétrico-magneto, como efeito Hall anômalo quântico, efeito magnetoelétrico topológico e aplicações relacionadas. Devido ao sinal de magnetismo fraco em uma película fina com isolador topológico dopado com elemento magnético fraco, estudos raros sobre as propriedades magnéticas intrínsecas do dopado com ímã foram relatados em isoladores topológicos dopados com elemento magnético e o acoplamento magnético relacionado não é bem explorado. Para entender as novas propriedades físicas intrínsecas do isolador topológico dopado com elemento magnético, especialmente a função do elemento magnético e o acoplamento de interação magnética relacionado, pode ser útil utilizar precisamente as propriedades do magneto na aplicação relacionada.

Neste trabalho, estudamos as propriedades magnéticas do isolador topológico Sb \ (_ {2} \) Te \ (_ {3} \) dopado com Ni-dopado por cristal único. Um loop de histerese com um baixo campo coercivo foi observado abaixo da temperatura de Néel (\ (T _ {\ mathrm {N}} \)). A suscetibilidade magnética revela um chute em \ (T _ {\ mathrm {N}} \) que é independente do campo magnético externo. A susceptibilidade magnética dos processos de resfriamento de campo zero e resfriamento de campo coincide acima \ (T _ {\ mathrm {N}} \), e eles são bifurcados abaixo \ (T _ {\ mathrm {N}} \). A divisão da susceptibilidade magnética é maior em campos magnéticos externos e temperaturas mais baixas. Não é mais observada divisão de susceptibilidade magnética em campos magnéticos acima de 7000 Oe. Nosso estudo confirma que essas características de suscetibilidade magnética se originam de uma ordem antiferromagnética acompanhada de ferromagnetismo fraco. A susceptibilidade saturada extraída vai bem com a tendência da cúspide de susceptibilidade magnética medida. Além da maioria dos relatos de que a cúspide de susceptibilidade magnética se origina da textura do spin do portador no ponto de Dirac do estado da superfície topológica, nossos resultados revelam que ela pode estar relacionada ao ferromagnetismo de elementos magnéticos.

Método Experimental

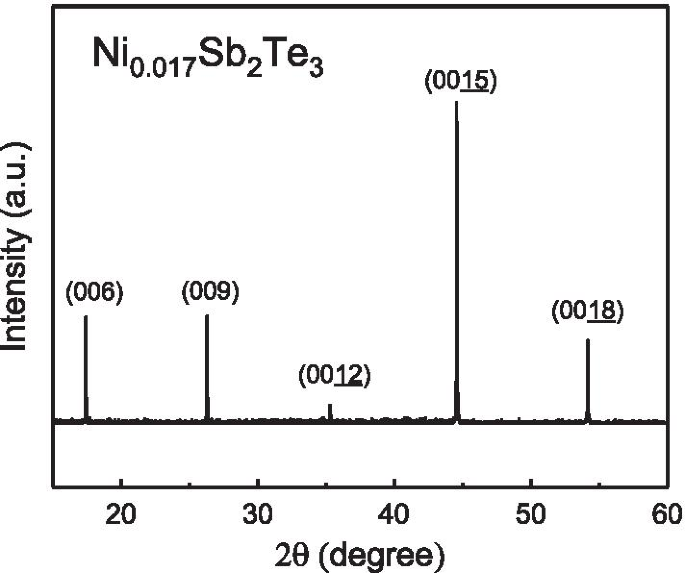
O espectro de XRD do cristal único Ni \ (_ {0.016} \) Sb \ (_ {2} \) Te \ (_ {3} \). Revela picos agudos e que sustentam a estrutura altamente monocristalizada

Cristais únicos de Sb \ (_ {2} \) Te \ (_ {3} \) foram cultivados com um forno caseiro de zona flutuante aquecida por resistência (RHFZ). As matérias-primas iniciais de Sb \ (_ {2} \) Te \ (_ {3} \) foram misturadas de acordo com a razão estequiométrica. No início, as misturas estequiométricas de elementos de alta pureza Ni (99,995%), Sb (99,995%) e Te (99,995%) foram derretidas a \ (700 \ sim 800 ^ {\ circ} \) C por 20 he depois lentamente resfriado à temperatura ambiente em um tubo de vidro de quartzo evacuado. O material foi usado como uma haste de alimentação para o seguinte experimento RHFZ. Nosso trabalho anterior sustenta que a uniformidade de cristal extremamente alta em cristais isolantes topológicos pode ser obtida através do método RHFZ. Após o crescimento, os cristais foram então resfriados em forno à temperatura ambiente. Os cristais crescidos foram clivados ao longo do plano basal, com uma superfície semelhante a um espelho prateado e brilhante, e então preparados para novos experimentos. Os resultados do espectro dispersivo de energia (EDS) suportam que \ (\ mathrm {Ni}:\ mathrm {Sb}:\ mathrm {Te} =0,017:2:3 \). A Figura 1 mostra o espectro de difração de raios-X (XRD). Ele revela picos agudos e esses picos são consistentes com o banco de dados de Sb \ (_ {2} \) Te \ (_ {3} \). Isso confirma que nossa amostra está altamente cristalizada. Espera-se que os átomos de Ni sejam uniformemente e aleatoriamente distribuídos em um único cristal. O tamanho do cristal é de 3 mm de comprimento, 2 mm de largura e 0,42 mm de espessura. As medições de magnetismo foram realizadas usando a técnica padrão em um aparelho comercial (Quantum Design MPMS) com um campo magnético de até 7 T. O campo magnético foi aplicado perpendicularmente à grande superfície clivada.

Resultados e discussão

A Figura 2 mostra a magnetização em função de campos magnéticos em diferentes temperaturas, e revelou a característica diamagnética em uma ampla gama de campos magnéticos e temperaturas. Este diamagnetismo vem do spin do portador e é consistente com os relatórios anteriores em isoladores topológicos BSTS [31]. Conforme mostrado na inserção superior direita, diferente dos relatórios anteriores, um loop de histerese foi observado em temperaturas abaixo de 125 K. O campo coercivo do loop de histerese mostra dependência fraca da temperatura e é de aproximadamente 50 Oe. A magnetização remanente e saturada do ciclo de histerese é de cerca de \ (10 ^ {- 5} \) emu / ge \ (10 ^ {- 4} \) emu / g a 100 K. O campo coercitivo baixo, o pequeno remanente , e a pequena magnetização saturada indica ferromagnetismo fraco. Conforme mostrado na inserção inferior esquerda, nenhum loop de histerese claro foi observado em temperaturas acima de 125 K. O ferromagnetismo se origina dos momentos magnéticos alinhados dos elementos magnéticos. A energia térmica pode randomizar o momento magnético alinhado e manchar o ferromagnetismo acima de uma temperatura crítica. Nossa observação indica que o sistema revela uma transição fraca de ferromagnetismo em torno de 120 K.

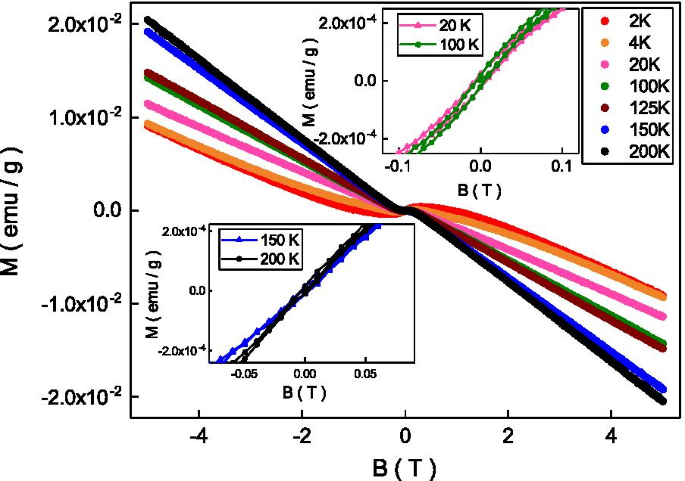
A susceptibilidade em função de campos magnéticos de 2 a 200 K. Revela o diamagnetismo em campos magnéticos elevados. Inserção superior direita:O loop de histerese foi observado em temperatura abaixo de 125 K. Inserção inferior esquerda:Nenhum loop de histerese foi observado em temperatura acima de 125 K

Para investigar a característica do magnetismo intrínseco da transição ferromagnética fraca observada, a susceptibilidade magnética dependente da temperatura foi realizada através de processos de resfriamento de campo e resfriamento de campo zero. A Figura 3 mostra a suscetibilidade magnética de processos resfriados por campo e resfriados por campo zero em diferentes campos magnéticos externos. A susceptibilidade magnética aumenta à medida que a temperatura diminui. Ele revela uma descontinuidade em 125 K (\ (T _ {\ mathrm {N}} \)) e o \ (T _ {\ mathrm {N}} \) é independente dos campos magnéticos externos. O \ (T _ {\ mathrm {N}} \) é a temperatura de Néel e o mecanismo detalhado será discutido e esclarecido abaixo. A suscetibilidade magnética de resfriado a campo e resfriado a campo zero coincide acima \ (T _ {\ mathrm {N}} \) e bifurca abaixo \ (T _ {\ mathrm {N}} \). Uma divisão de susceptibilidade magnética maior é observada em campos magnéticos externos mais baixos. Nosso resultado experimental mostra que esta descontinuidade e a divisão da susceptibilidade magnética não é mais observada em campos magnéticos superiores a 7000 Oe. É importante notar que a flutuação do sinal no campo magnético de 50 Oe é obviamente maior do que outros campos magnéticos. Uma das possíveis razões é que o alinhamento do momento magnético é metaestável em 50 Oe que está próximo ao campo coercivo do loop de histerese. Conforme mostrado na Fig. 2, o ciclo de histerese só foi observado abaixo de 125 K, que é o mesmo que a temperatura crítica da bifurcação de susceptibilidade magnética na Fig. 3. Isso indica que a divisão de susceptibilidade magnética observada pode estar relacionada ao ferromagnético fraco abaixo de \ (T _ {\ mathrm {N}} \). Sabe-se que o efeito ferromagnético seria manchado pela energia térmica e a susceptibilidade magnética acima da temperatura crítica poderia ser descrita pela lei de Curie-Weiss, \ (\ chi =\ chi _ {0} + \ frac {C} { T- \ theta} \), onde \ (\ chi \) é a susceptibilidade magnética medida, \ (\ chi _ {0} \) é a susceptibilidade magnética a 0 K, C é a constante de Curie que corresponde ao magneto de Bohr, T é a temperatura, e \ (\ theta \) é a temperatura de Curie [32]. A inserção da Fig. 4 mostra a dependência da temperatura do campo zero resfriado \ (\ frac {1} {\ chi - \ chi _ {0}} \) em diferentes campos magnéticos externos. O \ (\ frac {1} {\ chi - \ chi _ {0}} \) é proporcional a uma temperatura entre 125 e 250 K, e a inclinação é maior em campos magnéticos externos mais baixos. A inclinação está relacionada à constante de Curie. A extrapolação linear do \ (\ frac {1} {\ chi - \ chi _ {0}} \) entre 125 e 250 K de todos os campos magnéticos externos coincide em -125 K. Seguindo a lei de Curie-Weiss, este valor corresponde a \ (\ theta \). O negativo \ (\ theta \) (-125 K) indica que é um sistema antiferromagnético abaixo do \ (T _ {\ mathrm {N}} \) e \ (T _ {\ mathrm {N}} \) é conhecido como Temperatura de Néel [33]. O valor absoluto de \ (\ theta \) é consistente com o \ (T _ {\ mathrm {N}} \) observado na Fig. 3, e a temperatura crítica para observar o ciclo de histerese (125 K) na Fig. 2 . Estas observações indicam que o ferromagnetismo fraco e o antiferromagnetismo coexistem abaixo de \ (T _ {\ mathrm {N}} \).

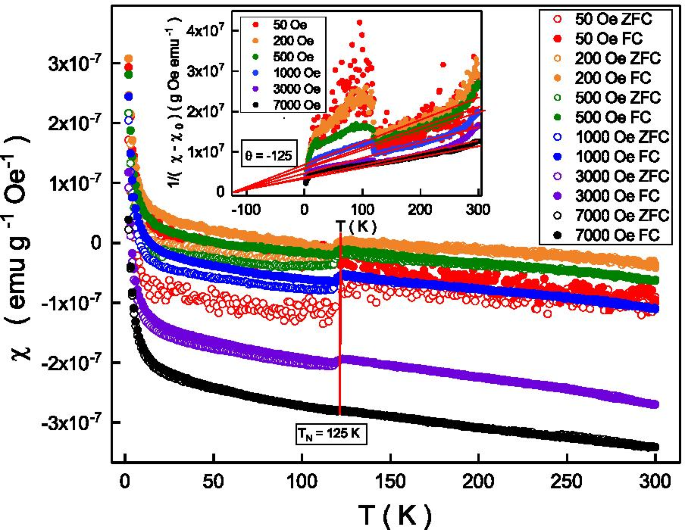
A suscetibilidade magnética de processos de resfriamento de campo e resfriamento de campo zero em diferentes campos magnéticos externos. A susceptibilidade magnética de campo resfriado e campo zero resfriado coincide acima de 125 K e bifurca abaixo de 125 K. Uma divisão de susceptibilidade magnética maior em campos magnéticos externos e temperaturas mais baixas. Não é mais observada divisão de susceptibilidade magnética em campos magnéticos acima de 7000 Oe. Inserção superior direita:a suscetibilidade magnética segue a lei de Curie-Weiss

Conforme mostrado na inserção da Fig. 3, a constante de Curie, C , é maior em campos magnéticos superiores. Seguindo a função paramagnética de Langevin, C pode ser expresso como \ (C =\ frac {N \ mu _ {0} \ mu ^ {2}} {3k _ {\ mathrm {B}} T} \) onde N é o número de elementos magnéticos por grama unitária, \ (\ mu \) é o momento efetivo de um elemento magnético, \ (\ mu _ {0} \) é a permeabilidade ao vácuo e \ (k _ {\ mathrm {B}} \) é a constante de Boltzmann [34]. O valor estimado de \ (\ mu \) em 200 Oe é cerca de 3,5 \ (\ mu _ {\ mathrm {B}} \) que está fechado para o valor teórico de 3,32 \ (\ mu _ {\ mathrm {B}} \ ) [35]. Isso confirma que o comportamento do magnetismo pode ser explicado pela lei de Curie-Weiss.

O momento magnético é congelado aleatoriamente no campo zero-cool e congelado ao longo da direção do campo magnético externo no campo-cool. A bifurcação da susceptibilidade magnética origina-se da anisotropia magnética. Esse recurso pode ser uma característica de uma ordem de antiferromagnetismo acompanhada por ferromagnetismo fraco; momentos ferromagnéticos de domínios congelam em uma direção aleatória no campo zero-frio, enquanto eles são forçados a se alinhar ao longo do campo magnético aplicado após o resfriamento em \ (T _ {\ mathrm {N}} \) no campo frio [36]. Como discutido acima, ele é composto por características ferromagnéticas e antiferromagnéticas fracas abaixo de \ (T _ {\ mathrm {N}} \) em nosso sistema. O fraco alinhamento ferromagnético quebraria ligeiramente a ordem do antiferromagnetismo e induziria a anisotropia magnética. A bifurcação da susceptibilidade magnética pode ser entendida como um ferromagnetismo fraco em um sistema antiferromagnético. Estes resultados suportam a bifurcação de susceptibilidade magnética observada abaixo de 125 K é a característica magnética do ferromagnetismo fraco em um sistema antiferromagnético. A divisão de suscetibilidade diferente em diferentes campos magnéticos externos pode se originar dos diferentes níveis de polarização parcial de antiferromagnetismo em campos magnéticos externos.

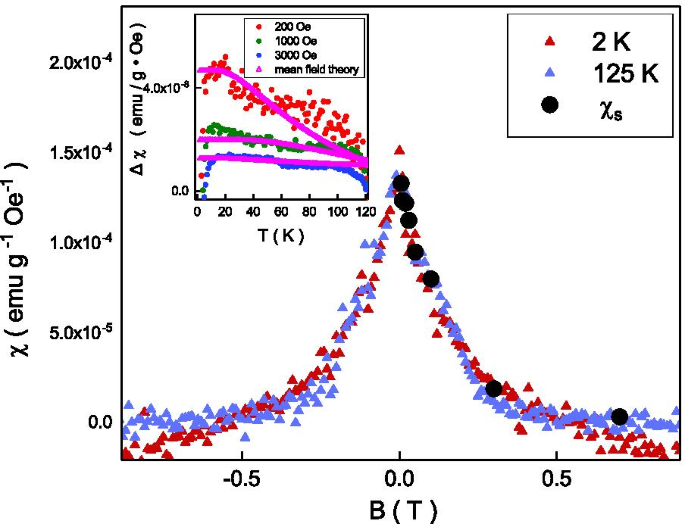
Inserção superior esquerda:A diferença de suscetibilidade magnética do campo resfriado e do campo zero resfriado segue a teoria do campo médio. A susceptibilidade saturada extraída vai bem com a tendência da cúspide de susceptibilidade magnética medida

Seguindo a teoria do campo médio, [37] o \ (T _ {\ mathrm {N}} \) está relacionado à força do acoplamento de troca, \ (J_ {0} \), e pode ser expresso como \ (T _ {\ mathrm {N}} =\ frac {S (S + 1)} {3k _ {\ mathrm {B}} T} J_ {0} \), onde S é o momento de rotação, \ (k _ {\ mathrm {B}} \) é a constante de Boltzmann. O \ (J_ {0} \) iria para \ (4,28 \ vezes 10 ^ {22} \) joule em nosso sistema com \ (T _ {\ mathrm {N}} \) =125 K. A teoria do campo médio apóia que a magnetização está relacionada à energia térmica por um fator de \ (e ^ {\ frac {-J_ {0} S} {k _ {\ mathrm {B}} T}} \). A susceptibilidade magnética pode ser expressa como \ (\ chi =\ chi _ {\ mathrm {S}} (1-e ^ {\ frac {-J_ {0} S} {k _ {\ mathrm {B}} T}} ) \), onde \ (\ chi _ {\ mathrm {S}} \) é a susceptibilidade magnética saturada. A divisão da susceptibilidade magnética, \ (\ chi _ {\ mathrm {FC}} - \ chi _ {\ mathrm {ZFC}} \) pode ser expressa como \ (\ chi _ {\ mathrm {S}} e ^ {\ frac {-J_ {0} S} {k _ {\ mathrm {B}} T}} \). O \ (\ chi _ {\ mathrm {S}} \) é sensível a campos magnéticos externos. Conforme mostrado na inserção da Fig. 4, esta equação poderia explicar nosso resultado experimental bem em uma ampla gama de temperaturas e campos magnéticos externos. O \ (\ chi _ {\ mathrm {S}} \) extraído é uma função de campos magnéticos externos. Para examinar melhor o resultado, a susceptibilidade dependente do campo magnético é realizada em temperaturas abaixo de \ (T _ {\ mathrm {N}} \), e mostra uma cúspide em campos magnéticos zero. Esta cúspide de susceptibilidade magnética no campo magnético zero é amplamente observada em materiais topológicos, e especula-se que se origine da textura de spin alinhada livre no ponto de Dirac [38]. A espectroscopia de fotoemissão com resolução de ângulo (ARPES) revela que o nível de Fermi está abaixo do ponto de Dirac em nosso Sb \ (_ {2} \) Te \ (_ {3} \) [39]. A cúspide observada não deve originar-se da textura de spin no ponto de Dirac. Por outro lado, o campo coercitivo do ciclo de histerese é de cerca de 50 Oe, que é duas ordens de magnitude menor do que a largura total na metade do máximo da cúspide, 0,4 T, e o ciclo de histerese não deve ser a principal fonte da cúspide observada . Como mostrado na inserção da Fig. 4, o campo magnético extraído dependente \ (\ chi _ {\ mathrm {S}} \) segue a mesma tendência do campo magnético da susceptibilidade magnética medida. Isso indica que a cúspide de suscetibilidade amplamente observada pode se originar da ordem antiferromagnética acompanhada por um alinhamento de ferromagnetismo fraco.

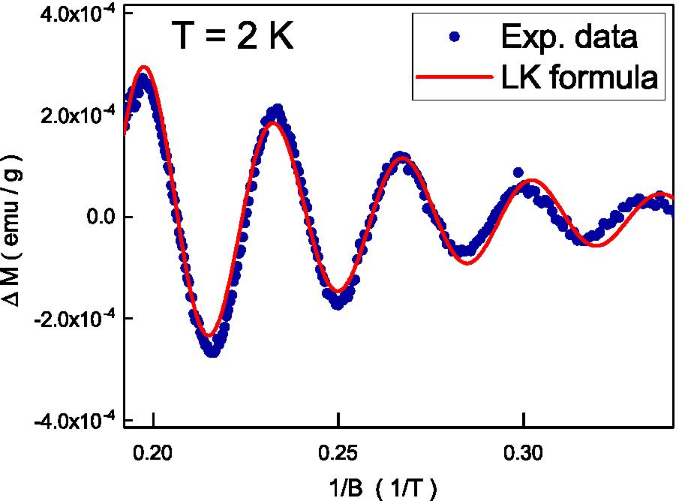
As oscilações do dHvA em função de campos magnéticos inversos. O resultado experimental se encaixa bem com a equação teórica

Após a análise, a bifurcação de susceptibilidade origina-se do magnetismo de ordem ferromagnetismo fraco acompanhado de antiferromagnetismo. A divisão da susceptibilidade magnética está relacionada à anisotropia magnetocristalina. Com isso, estimamos ainda a energia da anisotropia magnetocristalina, \ (\ Delta E =\ frac {M _ {\ mathrm {S}} H _ {\ mathrm {C}} V} {2} \), onde \ (H _ {\ mathrm {C}} =50 \) Oe, \ (M _ {\ mathrm {S}} =1,81 \ vezes 10 ^ {- 11} \) J / T e \ (V =2,5 \ vezes 10 ^ {- 9} \ ) m \ (^ {3} \) em nosso sistema, e o \ (\ Delta E \ sim 1,13 \ vezes 10 ^ {22} \) Joule [40]. Seguindo a energia do momento magnético, \ (g \ mu _ {\ mathrm {B}} B \), pode-se estimar que a energia da anisotropia cristalina magneto será menor do que a energia do momento magnético em \ (B> 0,61 \) T. Isso é consistente com nossa observação de que a divisão da suscetibilidade magnética não é mais observada em campos magnéticos externos acima de 0,7 T.

A Figura 5 mostra a susceptibilidade magnética em função de 1 / B e mostra oscilações periódicas. Isso é conhecido como oscilações de efeito De Haas-Van Alphen (dHvA) que se originam do movimento orbital do elétron itinerante em campos magnéticos elevados [41]. Analisamos as oscilações do dHvA ajustando a magnetização oscilatória à fórmula de Lifshitz-Kosevich (LK) [42], \ (\ Delta M \ propto -R \ sin [2 \ pi (\ frac {F} {B} - \ delta _ {p})] \). R está relacionado à taxa de espalhamento da portadora, efeito Zeeman e alargamento do nível de Landau [43]. A oscilação é descrita por um termo senoidal que contém o fator de fase \ (\ delta _ {p} \). \ (\ delta _ {p} \) está relacionado com a fase Berry (\ (\ Phi _ {B} \)), \ (\ delta _ {p} =\ frac {1} {2} - \ frac { \ Phi _ {B}} {2 \ pi} \). A dimensão do bolso Fermi caracteriza o valor \ (\ delta _ {p} \). Como mostrado na Fig. 5, a equação teórica se encaixa bem com nosso resultado experimental e os extraídos \ (\ delta _ {p} =0,43 \) e \ (F =29,8 \) T. Isso é consistente com a previsão teórica e a O dHvA observado vem do estado topológico da superfície. Seguindo a relação Onsager [44], \ (F =\ frac {\ hbar K_F ^ {2}} {2 \ pi} \), pode-se estimar que \ (K_ {F} =0,030 \) Å ^- ¹ é consistente com o valor relatado do ARPES. Esses resultados sugerem que as oscilações do dHvA se originam do estado topológico da superfície.

Conclusão

Neste trabalho, estudamos o comportamento magnético do monocristal isolante topológico Sb \ (_ {2} \) Te \ (_ {3} \) dopado com Ni-dopado Sb \ (_ {3} \). Um loop de histerese com baixo campo coercivo foi observado abaixo da temperatura de Néel. A suscetibilidade magnética revela um chute na temperatura de Nèel que é independente do campo magnético externo. A suscetibilidade magnética dos processos de resfriamento de campo zero e resfriamento de campo estão coincidindo acima da temperatura de Néel, e eles estão bifurcados abaixo da temperatura de Néel. A divisão da susceptibilidade magnética é maior em um campo magnético externo inferior. Não se observa mais divisão de suscetibilidade magnética quando a energia da anisotropia do momento magnético é menor do que a energia do momento magnético a 0,7 T. Nosso estudo sustenta que essas características de suscetibilidade magnética se originam de uma ordem antiferromagnética acompanhada por ferromagnetismo fraco. A susceptibilidade magnética saturada extraída vai bem com a tendência da cúspide de susceptibilidade magnética medida. Isso indica que a cúspide de suscetibilidade amplamente observada pode se originar do ferromagnetismo fraco. A oscilação do dHvA é consistente com a previsão teórica. Isso apóia que a oscilação observada do dHvA vem do estado da superfície topológica.

Disponibilidade de dados e materiais

Os conjuntos de dados gerados durante e / ou analisados durante o estudo atual estão disponíveis nos autores correspondentes mediante solicitação razoável.

Abreviações

XPD:: Difração de raios X
EDS:: Espectroscopia de raios-X de dispersão de energia
ARPES:: Espectroscopia de fotoemissão de ângulo resolvido
dHvA:: De Haas-Van Alphen

Demonstração de um biossensor flexível à base de grafeno para detecção sensível e rápida de células cancerosas do ovário Nano e ânodo de bateria:uma revisão

Nanomateriais

Materiais Poliméricos

biológico

Corante

Especiarias