Transporte Spin-Polarizado e Efeito Spin Seebeck em Pontos Quânticos Triplo com Acoplamentos Interdot Dependentes de Spin

Resumo

Estudamos o transporte eletrônico e termoelétrico dependente de spin através de uma estrutura composta de pontos quânticos triplos (TQDs) acoplados a dois terminais metálicos na presença de acoplamentos interdot dependentes de spin, que são confiáveis pela aplicação de um campo magnético estático nas junções do túnel entre pontos diferentes. Quando os TQDs estão conectados em série, um 100 % condutância polarizada por spin e energia termelétrica surgem mesmo para polarização de spin muito pequena do acoplamento entre pontos, pois os pontos são fracamente acoplados uns aos outros. Ao passo que se os TQDs estiverem conectados em forma de anel, a antirressonância de Fano resultará em picos agudos na condutância e na termopotência. Na presença de acoplamentos interdot dependentes de spin, os picos das termopares de spin-up e spin-down irão mudar para direções opostas no regime de nível de ponto, resultando em grande ou 100 % termopares de spin polarizadas ou puras. Este último geralmente surge em baixas temperaturas e é robusto contra o nível de desafinação, o acoplamento ponto-chumbo e a temperatura de equilíbrio do sistema.

Introdução

Junto com o desenvolvimento da spintrônica [1–3], a caloritrônica de spin [4, 5] tem recebido muita atenção nas últimas duas décadas. Na spintrônica, uma das questões mais atraentes é controlar o spin do elétron por polarização elétrica. Enquanto na caloritrônica de spin, o método de controle de spin é principalmente a polarização térmica, um gradiente de temperatura aplicado entre as diferentes extremidades do sistema. É considerada uma combinação de spintrônica e termoeletricidade. De particular interesse é o efeito Seebeck de spin (SSE), que gera corrente de spin pura sem o acompanhamento da contraparte de carga, ou polarização de spin caracterizado pela divisão de potenciais químicos de spin-up e spin-down. Ele abre uma maneira de utilizar o excesso de calor gerado em nanoestruturas para obter menor consumo de energia e melhor desempenho em dispositivos térmicos. Esse tipo de dispositivo também é eficaz na detecção do gradiente de temperatura do sistema com a ajuda do grau de liberdade de rotação dos portadores. Desde 2008, alguns grandes avanços experimentais da observação de ESS foram continuamente relatados por K. Uchida et.al. em metais magnéticos [6], isoladores ferromagnéticos [7, 8] e metais ferromagnéticos [9]. Foi posteriormente estudado em semicondutores ferromagnéticos [10], materiais não magnéticos com um campo magnético [11], materiais paramagnéticos [12], materiais antiferromagnéticos [13], interface isolante metal-ferromagneto [14] e também isoladores topológicos [15-17 ]

Foi provado por Mahan e seu colega de trabalho que uma forma semelhante a delta da função de transmissão, que é comum em sistemas de baixa dimensão, aumentará notavelmente a eficiência de dispositivos termoelétricos [18]. Desde então, o ponto quântico de dimensão zero (QD) [19, 20] em que os transportes estão confinados em todas as três dimensões foi extensivamente estudado para aumentar o coeficiente SSE (termopotência de spin), que indica a magnitude do viés de spin gerado sob a condição de circuito aberto pela polarização térmica infinitamente pequena [4-6]. Especialmente, se houver mais de um caminho de transmissão no sistema, os elétrons irão interferir uns com os outros e podem surgir os interessantes efeitos Dick [21, 22] ou Fano [23, 24] caracterizados por uma mudança brusca da função de transmissão e condutância . Portanto, muito trabalho tem sido dedicado à investigação de SSE em várias estruturas em forma de anel ou de caminhos múltiplos contendo QDs [25–33]. Os parâmetros ricos nele, como os níveis de pontos sintonizáveis, interação Coulomb, fluxo magnético, interações spin-órbita, assimetria dos acoplamentos ponto-chumbo permitem o controle efetivo dos processos de interferência quântica, resultando em termelétricas de spin gigante cuja magnitude pode chegar a tão alto ou até mais alto do que aquele de carga.

Triplo QDs (TQDs) com várias formas foram preparados em experimentos e teoricamente estudados que se concentram no diagrama de estabilidade, retificação de carga, frustração de carga, efeito de interferência quântica e controle de spin coerente [34-46]. Dentre eles, os pontos conectados em forma de anel são mais interessantes devido à existência de efeito de interferência quântica [39-46]. Em comparação com o transporte de elétrons, o efeito termoelétrico, especialmente SSE, raramente foi estudado em TQDs. No presente artigo, investigamos o SSE em TQDs levando em consideração os acoplamentos interdot dependentes de spin (ver Fig. 1). Ao aplicar um campo magnético estático nas junções do túnel entre os QDs, o spin do elétron realiza a precessão de Larmor e os acoplamentos interdot tornam-se dependentes do spin [47, 48]. Recentemente, também foi proposto que, utilizando campos magnéticos oscilantes e tensões de porta controladas temporalmente, pode-se separar as funções de onda de elétrons de diferentes componentes de spin em diferentes QDs, induzindo a velocidade de transferência resolvida por spin (força de acoplamento) [49, 50]. Em alguns trabalhos anteriores, os efeitos do acoplamento interdot dependente de spin na geração de corrente de spin já foram investigados [51, 52]. Aqui, mostramos que ele pode mudar as posições das termopares de spin-up e spin-down para direções opostas no espaço de nível de ponto, alterando os estados de antirressonância de Fano, resultando em 100 % termopares polarizadas de spin ou de spin puro, cuja magnitude pode ser tão grande quanto a de carga. Tal efeito é bastante diferente do caso de acoplamento interdot independente de spin [53, 54]. Curiosamente, os resultados obtidos podem ser cumpridos com uma polarização de spin muito pequena dos acoplamentos entre pontos.

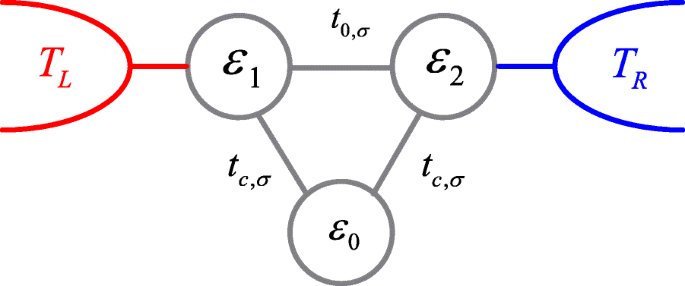
Gráfico esquemático do sistema de pontos quânticos triplo. Ao aplicar um campo magnético estático nas barreiras do túnel entre os pontos, os acoplamentos interdot tornam-se dependentes do spin

Modelo e métodos

O Hamiltoniano dos TQDs mostrados na Fig. 1 conectado a duas derivações pode ser modelado pelo seguinte Hamiltoniano de Anderson [25, 33, 51, 52],
$$ \ begin {alinhados} H =\! \! \ sum \ limits_ {k \ beta \ sigma} \ varejpsilon_ {k \ beta} c_ {k \ beta \ sigma} ^ {\ dag} c_ {k \ beta \ sigma} \! \, + \, \! \! \ sum \ limits_ {i \ sigma} \ varejpsilon_ {i} d_ {i \ sigma} ^ {\ dag} d_ {i \ sigma} \! \, + \ , \! \! \ sum \ limits _ {\ sigma} \! (t_ {0, \ sigma} d_ {1 \ sigma} ^ {\ dag} d_ {2 \ sigma} \! \, + \, t_ {c , \ sigma} d_ {1 \ sigma} ^ {\ dag} \! d_ {0 \ sigma} \\ + t_ {c, \ sigma} d_ {0 \ sigma} ^ {\ dag} d_ {2 \ sigma} \! \, + \, Hc) \, + \, \! \! \ Sum \ limits_ {k, \ sigma} \ left (V_ {kL} c_ {kL \ sigma} ^ {\ dag} d_ {1 \ sigma} \! \, + \, \! V_ {kR} c_ {kR \ sigma} ^ {\ dag} d_ {2 \ sigma} \! \, + \, \! Hc \ right), \ end {alinhado } $$ (1)
onde \ (c_ {k \ beta \ sigma} ^ {\ dag} \ left (c_ {k \ beta \ sigma} \ right) \) com β = L , R e \ (d_ {i \ sigma} ^ {\ dag} \ left (d_ {i \ sigma} \ right) \) com i =0,1,2 são respectivamente os operadores de criação (aniquilação) na liderança- β e ponto- i com rotação σ . Assumimos que cada ponto inclui um único nível de energia ε _i e negligencia a interação de Coulomb entre os elétrons nos pontos e nas derivações. QD-1 e QD-2 são acoplados um ao outro pelo acoplamento interdot t _{0, σ} = t ₀ (1+ σ p ) e para as derivações esquerda e direita pelo acoplamento ponto-derivação V _kL e V _kR , respectivamente. O QD-0 está conectado a QD-1 e QD-2 com força t _{c , σ} = t _c (1+ σ p ), onde σ =± 1 para elétrons spin-up e spin-down, respectivamente.

No regime de resposta linear, podemos escrever individualmente as correntes elétricas e de calor dependentes de spin sob uma diferença de potencial infinitamente pequena Δ V e uma diferença de temperatura Δ T entre as derivações esquerda e direita como [25, 33]
$$ \ begin {array} {* {20} l} &&J_ {e, \ sigma} =- e ^ {2} K_ {0, \ sigma} \ Delta V + \ frac {e} {T} K_ {1, \ sigma} \ Delta T, \ end {array} $$ (2) $$ \ begin {array} {* {20} l} &&J_ {h, \ sigma} =eK_ {1, \ sigma} \ Delta V- \ frac {1} {T} K_ {2, \ sigma} \ Delta T, \ end {array} $$ (3)
onde e é a carga do elétron e T a temperatura de equilíbrio do sistema. Os coeficientes K _{n , σ} na equação acima são dados por [25, 33]
$$ \ begin {array} {@ {} rcl @ {}} K_ {n, \ sigma} =\ frac {1} {\ hbar} \ int (\ varepsilon- \ mu) ^ {n} [- \ frac {\ partial f (\ varepsilon, \ mu)} {\ partial \ varepsilon}] T _ {\ sigma} (\ varepsilon) \ frac {d \ varejpsilon} {2 \ pi}, \ end {array} $$ (4 )
onde \ (\ hbar \) é a constante de Planck reduzida, μ o potencial químico dos condutores, f ( ε , μ ) =1 / {1 + exp [( ε - μ ) / k _B T ]} a função de distribuição de Fermi com constante de Boltzmann k _B .

Na Eq. (4), o coeficiente de transmissão T _σ ( ε ) para cada componente de spin pode ser obtido em termos da função de Green retardada como [25, 33] \ (T _ {\ sigma} (\ varepsilon) =\ Gamma _ {L} \ Gamma _ {R} \ left | G_ { 21, \ sigma} ^ {r} (\ varepsilon) \ right | ^ {2} \), onde \ (\ Gamma _ {L (R)} =2 \ pi \ sum _ {k} | V_ {kL ( R)} | ^ {2} \ delta \ left [\ varepsilon - \ varepsilon _ {kL (R)} \ right] \) é a função de largura de linha. Aplicando o método da equação de movimento, podemos facilmente derivar a forma analítica de \ (G_ {21, \ sigma} ^ {r} (\ varepsilon) \) como [55, 56]
$$ G_ {21, \ sigma} ^ {r} (\ varepsilon) =\ frac {\ left (\ varepsilon- \ varepsilon_ {0} \ right) t_ {0, \ sigma} + t_ {c, \ sigma} ^ {2}} {\ left (\ varepsilon- \ varepsilon_ {0} \ right) \ left (\ tilde {\ varepsilon} _ {1} \ tilde {\ varepsilon} _ {2} -t_ {0, \ sigma } ^ {2} \ right) -t_ {c, \ sigma} ^ {2} \ left (\ tilde {\ varejpsilon} _ {1} + \ tilde {\ varepsilon} \ right) -2t_ {0, \ sigma } t_ {c, \ sigma} ^ {2}}, $$ (5)
onde \ (\ tilde {\ varepsilon} _ {1 (2)} =\ varejpsilon - \ varejpsilon _ {1 (2)} + i \ Gamma _ {L (R)} / 2 \). O coeficiente de transmissão é obtido como [55, 56]
$$ \ begin {array} {@ {} rcl @ {}} T _ {\ sigma} (\ varepsilon) =\ frac {\ Gamma_ {L} \ Gamma_ {R} [\ left (\ varejpsilon- \ epsilon_ {0 } \ right) t_ {0, \ sigma} + t_ {c, \ sigma} ^ {2}] ^ {2}} {\ left | \ left (\ varepsilon- \ varepsilon_ {0} \ right) \ left ( \ tilde {\ varepsilon} _ {1} \ tilde {\ varepsilon} _ {2} -t_ {0, \ sigma} ^ {2} \ right) -t_ {c, \ sigma} ^ {2} \ left ( \ tilde {\ varepsilon} _ {1} + \ tilde {\ varepsilon} \ right) -2t_ {0, \ sigma} t_ {c, \ sigma} ^ {2} \ right | ^ {2}}, \ end {array} $$ (6)
A energia térmica (coeficiente de Seebeck) de cada componente de rotação S _σ é calculado sob a condição de desaparecimento da corrente de carga J _e = J _{e , ↑} + J _{e , ↓} =0, e é dado por [25, 33] S _σ =- K _{1, σ} / ( e T K _{0, σ} ), e a energia termelétrica de carga (rotação) é fornecida por S _{c ( s )} = S _↑ + (-) S _↓ .

Resultados e discussões

Nos seguintes cálculos numéricos, escolhemos a função de largura de linha Γ _L = Γ _R = Γ ₀ =1 como a unidade de energia e fixa μ =0 como o ponto zero de energia. As constantes de e , k _B e h estão todos configurados para ser 1. A Figura 2 mostra a condutância dependente do spin G _σ e energia termelétrica S _σ como funções do nível de ponto ε ₀ = ε ₁ = ε ₂ para t ₀ =0, ou seja, os TQDs estão conectados em série. Quando os acoplamentos interdot são independentes de spin ( p =0), as condutâncias de spin-up e spin-down em (a) e (b) são as mesmas e desenvolvem um pico centrado em ε ₀ =0 (linhas sólidas pretas).

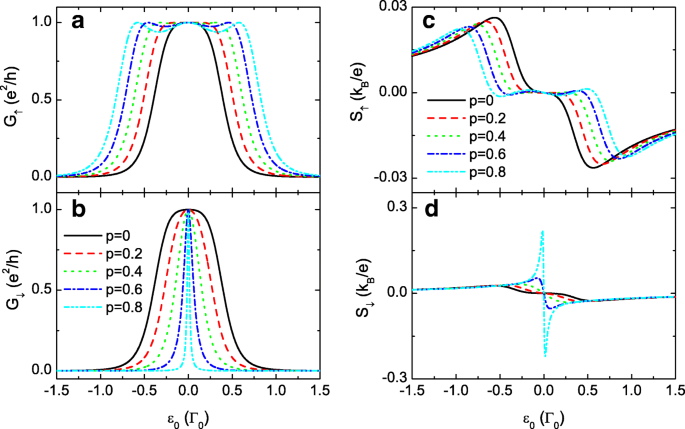
Condutância e energia térmica para t ₀ =0. Condutância polarizada spin G _σ em a e b , e energia termelétrica S _σ em c e d como funções do nível de ponto ε ₀ para t fixo ₀ =0 e diferentes valores de spin-polarização dos acoplamentos interdot. Os outros parâmetros são desafinação de nível Δ =0, temperatura T =0,001 e t _c =0,3

Na presença do acoplamento interdot dependente de spin p ≠ 0, o pico único da condutância de spin-up G _↑ na Fig. 2a evolui para uma configuração de pico triplo com valor de pico máximo inalterado devido ao acoplamento interdot de spin-up aprimorado t _{c , ↑} . Considerando que G _↓ permanece o padrão de pico único com largura de pico reduzida devido ao menor t _{c , ↓} . Para t _{0, σ} =0 e níveis de QDs idênticos ( ε ₁ = ε ₂ = ε ₀ ), o coeficiente de transmissão na Eq. (6) se reduz a
$$ \ begin {array} {@ {} rcl @ {}} T _ {\ sigma} (\ varepsilon) =\ frac {\ Gamma_ {0} ^ {2} t_ {c, \ sigma} ^ {4}} {\ left \ {\ left (\ varepsilon- \ varepsilon_ {0} \ right) \ left [\ left (\ varepsilon- \ varepsilon_ {0} \ right) ^ {2} - \ Gamma_ {0} ^ {2} / 4 \ right] -2t_ {0, \ sigma} ^ {2} \ right \} ^ {2} + \ Gamma_ {0} ^ {2} t_ {c, \ sigma} ^ {4}}. \ end {array} $$ (7)
Existem três ressonâncias na função de transmissão localizadas respectivamente em ε = ε ₀ e \ (\ varepsilon =\ varepsilon _ {0} \ pm \ sqrt {2t_ {c, \ sigma} ^ {2} + \ Gamma _ {0} ^ {2} / 4} \). Sob a condição de baixa temperatura, três picos ressonantes emergem na condutância em ε ₀ = μ e \ (\ varepsilon _ {0} =\ mu \ pm \ sqrt {2t_ {c, \ sigma} ^ {2} + \ Gamma _ {0} ^ {2} / 4} \), respectivamente. Para o caso de acoplamento interdot fraco, os três picos se fundem em uma configuração de pico único, conforme mostrado pelas linhas pretas na Fig. 2a e. Com o aumento da polarização de spin interdot p , o valor de t _{c , ↑} = t _c (1+ p ) aumenta e os três picos na condutância de spin-up são separados no espaço de energia, como mostrado na Fig. 2a. Enquanto isso, a magnitude de t _{c , ↓} fica menor e G _↓ na Fig. 2b permanece um padrão de pico único em conformidade. Da Eq. (6) também se pode ver que a largura do pico é reduzida diminuindo t _{c , ↓} .

Quando p =0, as termopares de cada componente de spin na Fig. 2c e d são idênticas e antissimétricas com respectivas ao ponto de simetria elétron-buraco ( ε ₀ =0), o que é consistente com trabalhos anteriores [33, 57]. Devido à existência de gradiente de temperatura que gera o efeito termoelétrico, a temperatura do eletrodo esquerdo é maior que a do direito e há mais elétrons acima do potencial químico μ na liderança esquerda. Correspondentemente, existem mais furos abaixo de μ . Quando os níveis de energia dos QDs estão abaixo (acima) μ , os principais portadores são buracos (elétrons) e então a energia termelétrica é positiva (negativa) [57]. As termelétricas mudam seus sinais em ε ₀ =0 devido à compensação de elétrons e lacunas. Com o aumento de p , a largura do pico da termelétrica spin-up S _↑ é ampliado com valor de pico reduzido. Ao passo que o spin-down é reduzido. Curiosamente, o valor de pico de S _↓ é obviamente aprimorado pelo aumento de p . Para o caso de grande polarização de spin entre pontos, como p =0,8, o valor de pico de S _↓ é cerca de dez vezes de S _↑ com valor quase inalterado da condutância dependente do spin G _σ . Isso pode ser explicado da seguinte forma. Para p positivo , a taxa de tunelamento interdot t _{c , ↑}> t _{c , ↓} e os elétrons de spin-up (ou lacunas) passarão pelos QDs mais rápido do que os de spin-down. Correspondentemente, há mais elétrons de spin-down (buracos) sendo bloqueados nas derivações esquerda (direita) em comparação com os de spin-up, resultando em maior voltagem de spin-down em resposta ao gradiente de temperatura.

Para aumentar ainda mais a diferença entre S _↓ e S _↑ , apresentamos os resultados de p extremamente grandes na Fig. 3. Descobrimos que a condutância de spin-up G _↑ e energia termelétrica S _↓ são menos influenciados pela variação de p , que é mostrado pelas inserções na Fig. 3a e b para comparação. Com o aumento de p , os portadores de spin-down tornam-se ainda mais difíceis de transportar através dos QDs e serão acumulados nos terminais. Consequentemente, o valor de G _↓ é suprimido monotonamente, mas o valor de pico de S _↓ é notavelmente ampliado, sugerindo um meio eficaz para gerar uma energia termelétrica totalmente polarizada de spin pelo acoplamento interdot dependente de spin. Esse resultado também pode ser promissor na detecção do gradiente de temperatura no sistema pela técnica SSE. Agora que o acoplamento interdot fraco aumenta o valor da energia termelétrica, escolhemos t menor _c com p fixo =0,7 na Fig. 4. Neste caso, os três picos ressonantes nas condutâncias spin-up e spin-down emergem em um. A largura do pico da condutância é ampliada aumentando t _c o que está de acordo com os resultados anteriores. Fig. 4b e d mostra que a magnitude de ambos S _↑ e S _↓ é aprimorado diminuindo t _c . O máximo da energia termelétrica spin-down também pode atingir cerca de 4 k _B / e para t _c =0,02 Γ ₀ . Em experimentos, os acoplamentos interdot são ajustáveis pela tensão da porta ou pela espessura da barreira do túnel. Portanto, pode ser mais viável aumentar a energia termelétrica alterando t _c com uma polarização de spin fixa p , já que o campo magnético geralmente é mais difícil de ser controlado em comparação com o campo elétrico. Na verdade, grande energia termelétrica pode ser obtida com muito pequeno p sob algumas condições, conforme mostrado a seguir.

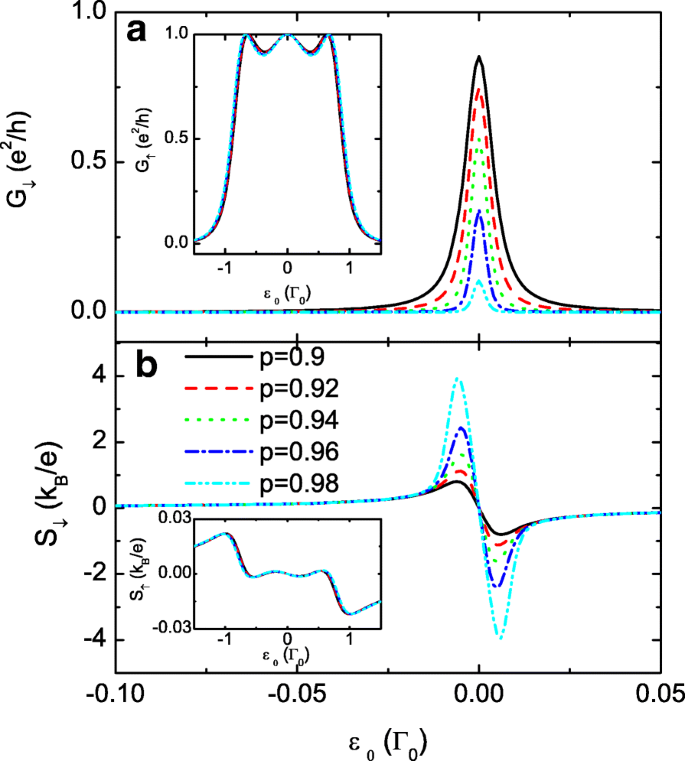
Condutância de spin-down e a energia termelétrica. A condutância de spin-down G _↓ em a e a energia termelétrica S _↓ em b para o caso de acoplamento interdot grande 1> p ≥0,9. A inserção em a é para G _↑ em um regime de nível de ponto grande e a inserção em b denota a energia termelétrica de aumento de rotação em comparação com a de redução de rotação. Os outros parâmetros são como na Fig. 2

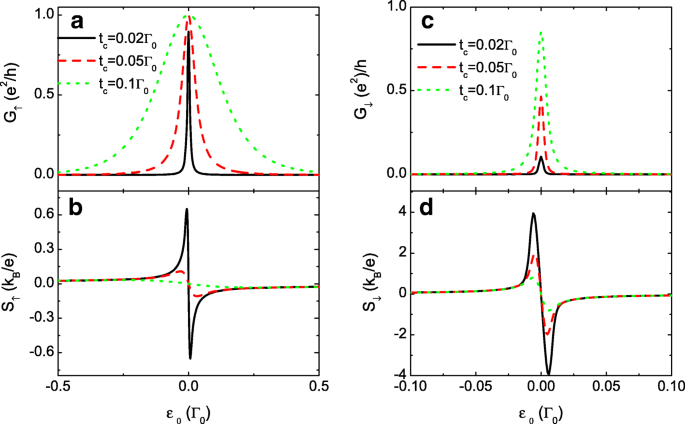
Condutância e energia termelétrica para diferentes t _c . Condutância polarizada spin G _σ em a e c , e a energia termelétrica S _σ em b e d como funções do nível de ponto ε ₀ para p =0,7 e diferentes valores de t _c . Os outros parâmetros são como na Fig. 2

Se os QDs estiverem conectados em forma de anel, o efeito Fano surgido mudará drasticamente as propriedades da condutância [46] e da energia termelétrica. Particularmente, a termopumagem gigante ocorre em torno do estado de antirressonância de Fano, onde a função de transmissão se aproxima de zero T _σ ( ε ) =0 devido à reflexão completa [25–33]. Substituindo a energia do elétron ε pelo potencial químico μ na Eq. (5), pode-se encontrar que o único estado de antirressonância está localizado em
$$ \ begin {array} {@ {} rcl @ {}} \ varepsilon_ {0} =\ mu + t_ {c, \ sigma} ^ {2} / t_ {0, \ sigma}, \ end {array} $$ (8)
que é determinado exclusivamente pelos acoplamentos interdot e independente de outros parâmetros, como os níveis de pontos ε ₁ , ε ₂ , temperatura T ou a matriz híbrida ponto-chumbo Γ _α . Portanto, é bastante simples ajustar a condutância e as quantidades termoelétricas em um sistema tão complexo. Sob a condição de μ =0, o estado de antirressonância localiza-se apenas em ε positivo ₀ lateral. As Figuras 5a eb mostram o vale de antirressonância de Fano na condutância. A inserção na Fig. 5a mostra a forma de linha de Fano da condutância em um regime de nível de ponto grande. Ao contrário do caso de t ₀ =0 em que o ponto zero da energia termelétrica localiza-se em ε ₀ =0, o de t ₀ ≠ 0 está no estado antirressonante, respectivo ao qual a termopagem é antissimétrica. Para o caso de p =0, os pontos zero das termelétricas de ambos os componentes de spin estão em ε ₀ =0,09 como mostrado na Fig. 5c e d. Com o aumento de p , eles são separados e deslocados para direções opostas de 0,09. Um pico amplo com valores positivos e negativos emergem nos dois lados dos pontos zero, respectivamente. É importante mencionar que o valor da energia termelétrica é desprezivelmente pequeno nos outros regimes de nível de pontos, o que é mostrado na inserção da Fig. 5c. Tanto o deslocamento dos pontos zero quanto os picos nas termelétricas trazem dois resultados interessantes. Um é o 100 % termelétrica polarizada por spin quando os picos de S _↑ e S _↓ estão totalmente separados no espaço de energia por bastante grandes p valor. Veja, por exemplo, a linha azul tracejada e pontilhada na Fig. 5c e d para p =0,4. No lado direito de ε ₀ =0,09, o valor de S _↓ aproxima-se de zero, mas S _↑ tem dois picos agudos. Considerando que no lado esquerdo de ε ₀ =0,09, a energia termelétrica spin-down S _↓ tem dois picos com quase zero S _↑ .

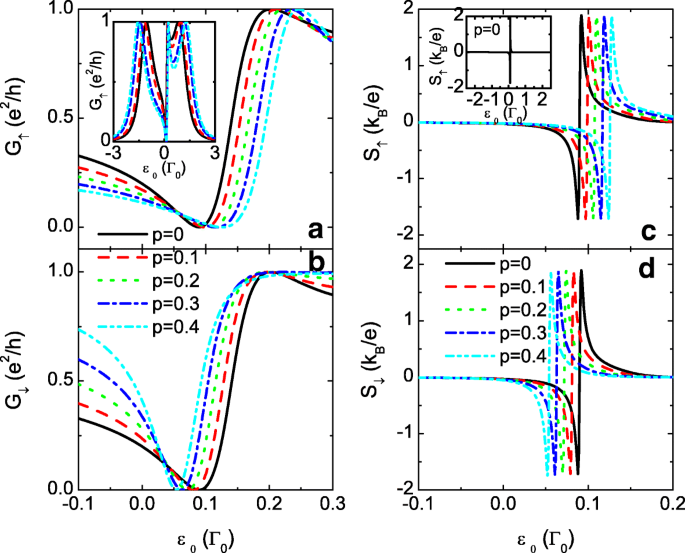
Condutância e energia termelétrica para t ₀ =1. Condutância polarizada spin G _σ em a e b , e a energia termelétrica S _σ em c e d como funções do nível de ponto ε ₀ para t ₀ =1, t _c =0,3 e diferentes valores da polarização de spin dos acoplamentos interdot p . As inserções em a e c são a condutância e a energia termelétrica em um regime de nível de ponto grande, respectivamente. Os outros parâmetros são como na Fig. 2

O outro resultado interessante é a energia termelétrica de spin puro, ou seja, S _s = S _↑ - S _↓ ≠ 0 enquanto S _e = S _↑ + S _↓ =0, ou corrente de spin pura em circuito fechado sob polarização térmica finita [58]. Isso significa que as termopares de spin-up e spin-down com igual magnitude têm sinais opostos. A magnitude de S _s é maximizado quando os picos agudos nas termelétricas spin-down e spin-up com sinais opostos se encontram ao mesmo ε ₀ ajustando a polarização de spin dos acoplamentos interdot p . Conforme mostrado na Fig. 6a, os pontos zero, bem como os picos em S _↑ e S _↓ são respectivamente deslocados para os lados direito e esquerdo de ε ₀ =90 k _B T devido a p ≠ 0. Como resultado disso, o pico negativo na termelétrica de spin-up e o pico positivo na termelétrica de spin-down emergem simultaneamente em torno de ε ₀ =90 k _B T induzindo a energia termelétrica pura de spin. Isso geralmente ocorre para pequenos p porque os dois picos estreitos em S _σ estão muito próximos dos pontos zero, o que é confirmado pela linha tracejada azul pontilhada na Fig. 6a com p =0,02. Para mostrar claramente a pequena energia dominante, escolhemos k _B T como a unidade de energia nele. Enfatizamos que esta energia termelétrica de spin puro pode ser obtida com uma polarização de spin muito pequena do acoplamento entre pontos, que é realizável pela aplicação de um campo magnético fraco nas barreiras do túnel. Além disso, a magnitude da energia termelétrica de spin puro é tão grande quanto a de carga (a linha pontilhada verde).

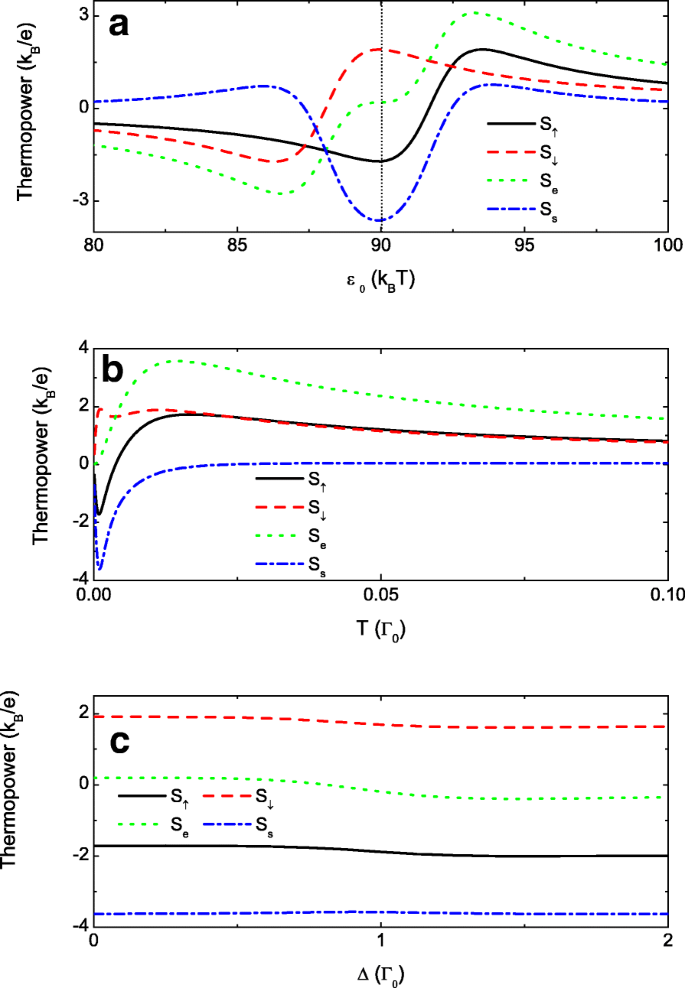
Regulamentações quânticas das termelétricas. As termopares variam com o nível de pontos em a , a temperatura em b e o nível de desafinação em c . Outros parâmetros são p =0,02, t ₀ =1 e t _c =0,3. O nível de pontos em b e c é escolhido como ε ₀ =0,09 Γ ₀ . O nível de desafinação Δ =0 em a e b , e a temperatura é T =0,001 em a e c

Finalmente, apresentamos o spin puro resolvido por spin e as termopares de carga variando com a temperatura T e o nível de desafinação Δ na Fig. 6b e d, respectivamente. O nível de pontos ε ₀ é escolhido como 0,09 para focar no vale antirressonância de Fano. A Figura 6b mostra que em baixa temperatura S _↑ e S _↓ desenvolver picos com sinais opostos denotados pelas linhas sólidas e tracejadas, resultando em termelétricas de rotação pura bastante grande S _s (linha tracejada-pontilhada azul). Agora, a energia termelétrica de carga S _e pode ser muito pequeno, conforme mostrado pela linha pontilhada verde. Com o aumento da temperatura, o efeito Fano é destruído pelo movimento térmico aleatório dos portadores e os picos em S _σ estão manchados. Como resultado disso, a diferença entre S _↑ e S _↓ é indistinguível, e a energia termelétrica pura de spin se aproxima de zero. A Figura 6d mostra que a termelétrica de spin puro é robusta contra a diferença entre os níveis de pontos Δ . Isso é consistente com o resultado da Eq. (7) que o estado antirressonante Fano é independente dos pontos 1 e 2.

Conclusões

Em conclusão, nós estudamos as propriedades da condutância elétrica e da energia termelétrica em um TQDs conectado em série ou circularmente com acoplamentos interdot dependentes de spin. É dada especial atenção à geração de 100 % termopares de spin polarizadas e puras. Verificou-se que o primeiro pode ser realizado na configuração de TQDs em série com polarização de spin de acoplamento interdot suficientemente grande quando os pontos estão fortemente acoplados uns aos outros. Ao passo que se os pontos estiverem fracamente acoplados, gigante 100 % A energia termelétrica polarizada por spin pode ser realizada sob uma polarização de spin de acoplamento interdot muito pequena. Quando os pontos estão em configuração circular, a energia termelétrica é antissimétrica com relação ao estado de antirressonância de Fano em torno do qual a energia termelétrica desenvolve picos agudos. Ao alterar a polarização de spin dos acoplamentos interdot, os picos em termopares de spin-up e spin-down são deslocados para direções opostas no regime de níveis de QDs. Agora, os 100 % As termopares de spin polarizadas e puras podem ser realizadas de uma maneira bastante fácil. Os presentes resultados podem ser obtidos sob pequeno valor de polarização de spin dos acoplamentos interdot, o que é favorável em experimentos.

Óxido de grafeno covalentemente modificado e polímero de microporosidade intrínseca (PIM-1) em membranas compostas de película fina de matriz mista Carbon Dots @ Platinum Porfirina Composto como Nanoagente Teranóstico para Terapia Eficiente Fotodinâmica do Câncer

Nanomateriais

Materiais Poliméricos

biológico

Corante

Especiarias